Тема Газпром

Стереометрия на Газпроме

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела газпром

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#99239

Для монтажа бурового оборудования в скважину используется подвес, состоящий из металлического каркаса в форме равностороннего треугольника и трёх регулируемых по длине тросов протянутых через вершины треугольника и соединяющихся на крюке. Расстояние между тросами на каркасе составляет $2$ м, а их первоначальная длина от каркаса до крюка — $3$ м. При спуске оборудования оказалось, что крюк нужно сместить на $√3 12$ м вдоль медианы каркаса по направлению от вершины. На сколько метров нужно удлинить трос, проходящий через эту вершину?

Источники: Газпром - 2024, 11.6 (см. olympiad.gazprom.ru)

Подсказки к задаче

Подсказка 1

Из условия следует, что у нас изначально есть правильный тетраэдр со стороной 2. После этого мы как-то меняем положение крюка, чтобы точка вершины сдвинулась вдоль медианы в основании на нужную длину. Подумайте, что это значит в терминах геометрии.

Подсказка 2

Это значит, что проекция вершины S на плоскость основания сместилась на нужную длину, но при этом проекция S всё равно лежит на медиане. Если S₁ — новая точка, то мы можем посчитать S₁O₁ как катет прямоугольного треугольника S₁DO₁, где D — середина BC, а O₁ — сдвинутая на нужную длину точка O. Но тогда мы можем найти и S₁A (из какого прямоугольного треугольника?), а значит, и разность длин троса. Ну и всё, идейно задача решена, осталось посчитать!

Показать ответ и решение

Пирамида $SABC$ — правильная, тогда медиана

√3 √ - AD = AB ⋅sin60∘ =2 ⋅2-= 3,

а апофема

∘ --------- ∘------ √- SD = SB2 − BD2 = 32− 12 = 2 2.

Так как $O$ — точка пересечения медиан треугольника $ABC$ , то

√- √- AO = 2AD = 2-3, DO = 1AD = -3. 3 3 3 3

При увеличении длины троса $SA$ проекция вершины пирамиды переместиться в точку $O1$ , так что $√- OO1 = 132$ , тогда

√ - √- √ - √- √- √ - AO1 = 2-3+ -3-= 3-3, DO1 = -3-− -3= --3. 3 12 4 3 12 4

Поскольку, при увеличении длины троса $SA$ до $SA 1$ длина апофемы треугольника $S BC 1$ равна $S D= SD 1$ , то

┌ ------------- ∘ --------2- ││∘ √ - ( √3)2 ∘ 125 5√5 S1O1 = S1D2− DO1 = (2 2)2− 4-- = 16-= -4-.

Следовательно,

┌ ---------------- ∘---------- ││ ( 5√5-)2 (3√3-)2 ∘-152 ∘ --- S1A = S1O21 + AO21 =∘ -4- + -4- = 16-= 9,5.

Тогда трос нужно удлинить на $√9,5− 3$ .

Ответ:

$√9,5− 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#99232

Десять шаров одинакового радиуса сложены в виде треугольной пирамиды так, что каждый шар касается как минимум трёх других. Найти радиус сферы, в которую вписана пирамида из шаров, если радиус шара, вписанного в центр пирамиды из шаров, касающегося шести одинаковых шаров, равен $√- 6− 1.$

Источники: Газпром - 2023, 11.6 (см. olympiad.gazprom.ru)

Показать ответ и решение

При таком расположении десяти одинаковых шаров центры $A,B,C,D$ четырёх из них расположены в вершинах правильного тетраэдра, а точки касания расположены на ребрах этого тетраэдра. Следовательно, ребро тетраэдра равно четырём радиусам этих шаров, радиус внешней сферы больше радиуса шара, описанного около тетраэдра на четверть длины ребра тетраэдра, а радиус внутреннего шара меньше расстояния от центра тетраэдра до его грани на эту же величину. Рассмотрим сечение тетраэдра плоскостью $ABM$ :

Обозначим длину ребра тетраэдра за $a$ , радиус сферы, описанной вокруг пирамиды из шаров за $R$ , радиус шара, вписанного в центр пирамиды из шаров за $r$ .

В треугольнике $ABM :$

√- √ - √- AM =BM = a-3, ME =MH = 1AM = a--3, AH = BE = 2AM = a-3, 2 3 6 3 3

следовательно,

√ - AE =BH =∘AM2--−-ME2-= 2√a-= a-6. 6 3

Из подобия треугольников $AEM$ и $AHO$ имеем

AO AH a√3 √2 √2- a√6 AM- =-AE = a√6 =-2-и AO =BO = -2-AM = -4--

В треугольнике $ABO$ :

SABO = AH-⋅BO-= AB-⋅FO, 2 2

следовательно,

√-- √- FO = AH-⋅BO-= a2-18= a-2. AB 12a 4

Тогда

a√6 a a(√6 +1) R =AO + AL = -4-+ 4 = ---4---- a√2 a a(√2 − 1) r= FO − FK = -4-− 4 = ---4----

Таким образом,

√ - - - R-= (√-6+-1)-=(√6 +1)(√ 2+1), r ( 2− 1)

откуда

R = (√6-+ 1)(√2+ 1)r= 5(√2+ 1).

Ответ:

$5(√2+ 1)$

Ошибка.
Попробуйте повторить позже

Задача 3#98163

В сферу радиуса $3$ вписана правильная треугольная призма $ABCA B C 1 1 1$ с основанием $ABC$ и боковыми ребрами $AA ,BB ,CC . 1 1 1$ Отрезок $CD$ — диаметр этой сферы. Найти объем призмы, если $√- AD = 2 6.$

Источники: Газпром - 2022, 11.6 (см. olympiad.gazprom.ru)

Подсказки к задаче

Подсказка 1

Нам нужно понять, от чего зависит конструкция, то есть какими параметрами задаётся. С учетом того, что нам надо найти объём, то есть найти площадь основания на высоту, какие параметры нам удобно ввести, чтобы через них всё выражалось?

Подсказка 2

Удобно ввести высоту и радиус окружностей, в которые вписано каждое из оснований. Тогда, поскольку в силу симметрии CD — диаметр, то нам известна длина CD, а также известна длина AD. Это значит, что у нас есть два уравнения на две переменных (r и h), поскольку есть два прямоугольных треугольника у которого стороны либо константы, либо выражаются через r и h. Осталось решить такую систему и посчитать объём!

Показать ответ и решение

Плоскости оснований $ABC$ и $A B C 1 1 1$ призмы пересекают сферу по окружностям, описанным около правильных треугольников $ABC$ и $A1B1C1;$ пусть их центры — точки $O$ и $O1$ соответственно.

Легко показать, что середина $M$ отрезка $OO1$ является центром сферы.

$PIC$

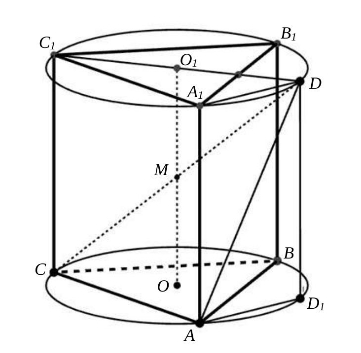
Проведем через точку $C1$ диаметр $C1D$ окружности с центром в точке $O1.$ Покажем, что $CD$ — диаметр сферы. Действительно, плоскость $CC1D$ перпендикулярна плоскостям основания и, значит, вместе с точкой $O1$ содержит отрезок $OO1.$ Т.к. $C1D = 2DO1,$ прямая $CD$ пересекает отрезок $OO1$ в его середине, т.е. в центре $M$ заданной сферы.

Пусть $D1$ — проекция точки $D$ на плоскость основания $ABC,$ высота призмы равна $h,$ а радиусы окружностей с центрами $O$ и $O1$ равны $r.$ Рассмотрим треугольники $CC1D$ и $ADD1.$ Учитывая, что $C1D = 2r,AD1 =r$ (треугольник $AOD1$ равносторонний), $CC1 = DD1 =h,$ по т. Пифагора получаем систему уравнений:

{ h2+4r2 = 62√ h2+r2 =(2 6)2

Решая систему, находим, что $√- r= 2,h =2 5.$ Тогда сторона основания равна $√ - 2 3,$ его площадь $√ - S =3 3,$ и следовательно, объем призмы $√-- V = S⋅h =6 15.$

Ответ:

$6√15$

Курсы

Всё необходимое для достижения цели

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Предыдущий раздел

Следующий раздел