03 Смежные и вертикальные углы
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Чему равна сумма смежных углов?
Источники:
Смежные углы всегда образуют развёрнутый угол, который равен
Ошибка.
Попробуйте повторить позже
Какие углы называются вертикальными?
Источники:
Вертикальные углы образуются при пересечении двух прямых и лежат напротив друг друга.
Ошибка.
Попробуйте повторить позже
Какое утверждение о вертикальных углах верное?
Источники:
Основное свойство вертикальных углов - они всегда равны.
Ошибка.
Попробуйте повторить позже
Если один из смежных углов равен то чему равен второй?
Источники:
Cумма смежных углов равна то есть
Ошибка.
Попробуйте повторить позже
Могут ли два смежных угла быть равными?
Источники:
Если два смежных угла равны, то каждый из них равен
Ошибка.
Попробуйте повторить позже
Найдите угол, смежный с углом в
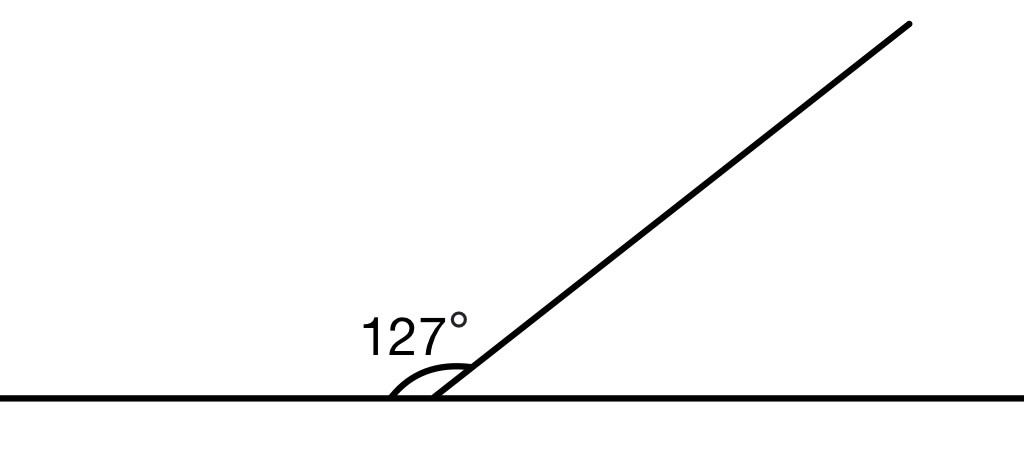
Источники:
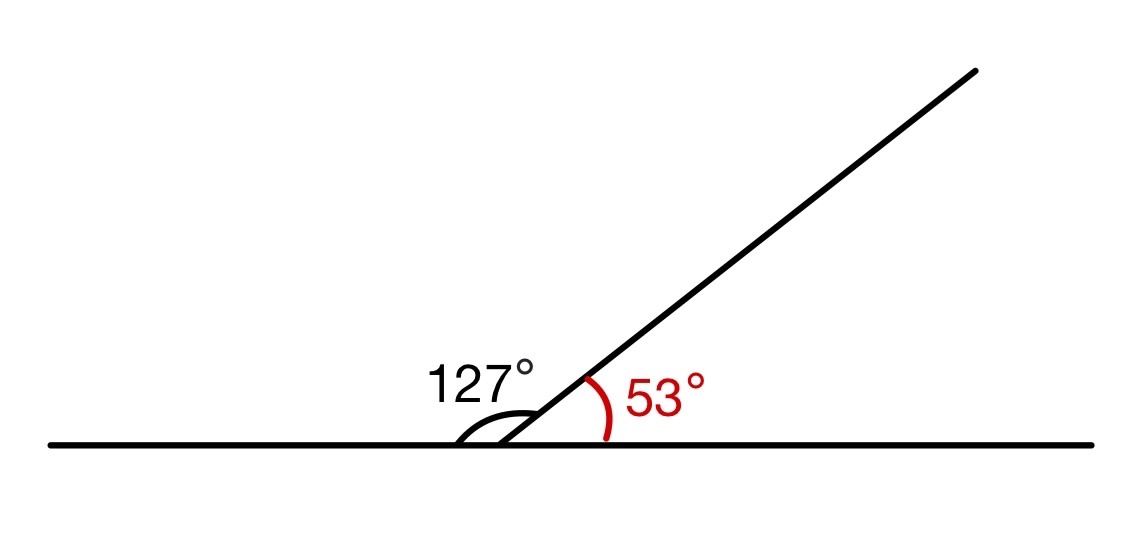
Сумма смежных углов равна то есть
Ошибка.
Попробуйте повторить позже
Найдите величину угла
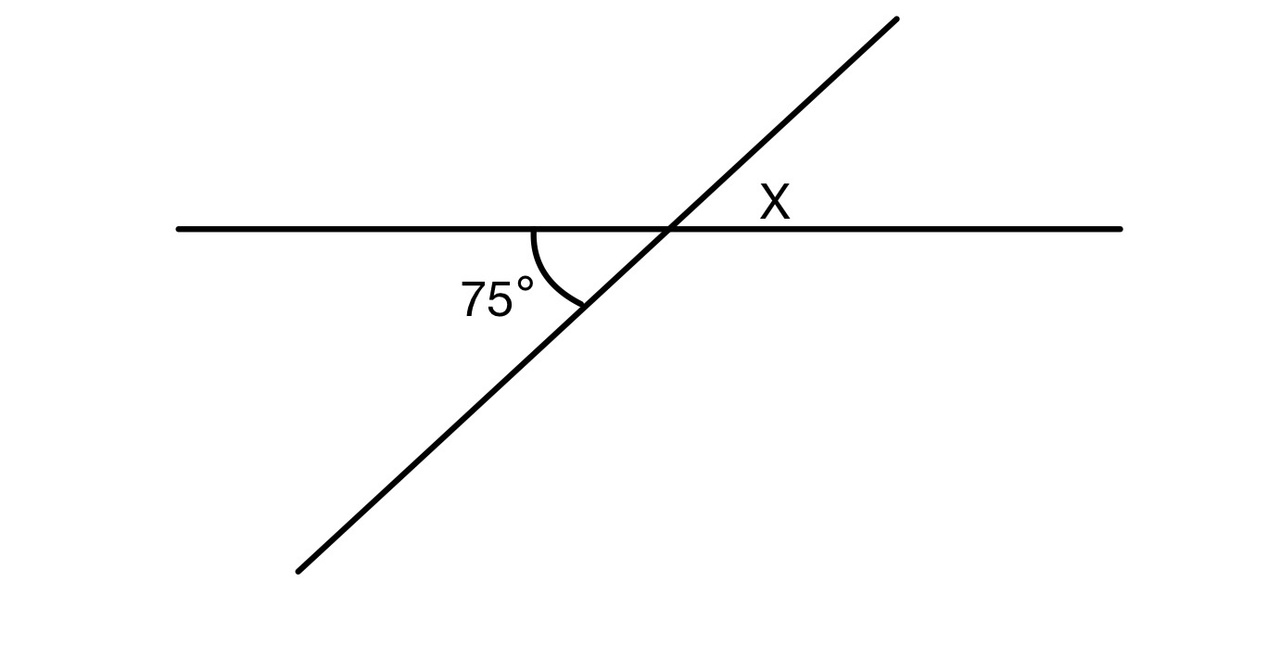
Источники:
Вертикальные углы равны, поэтому
Ошибка.
Попробуйте повторить позже
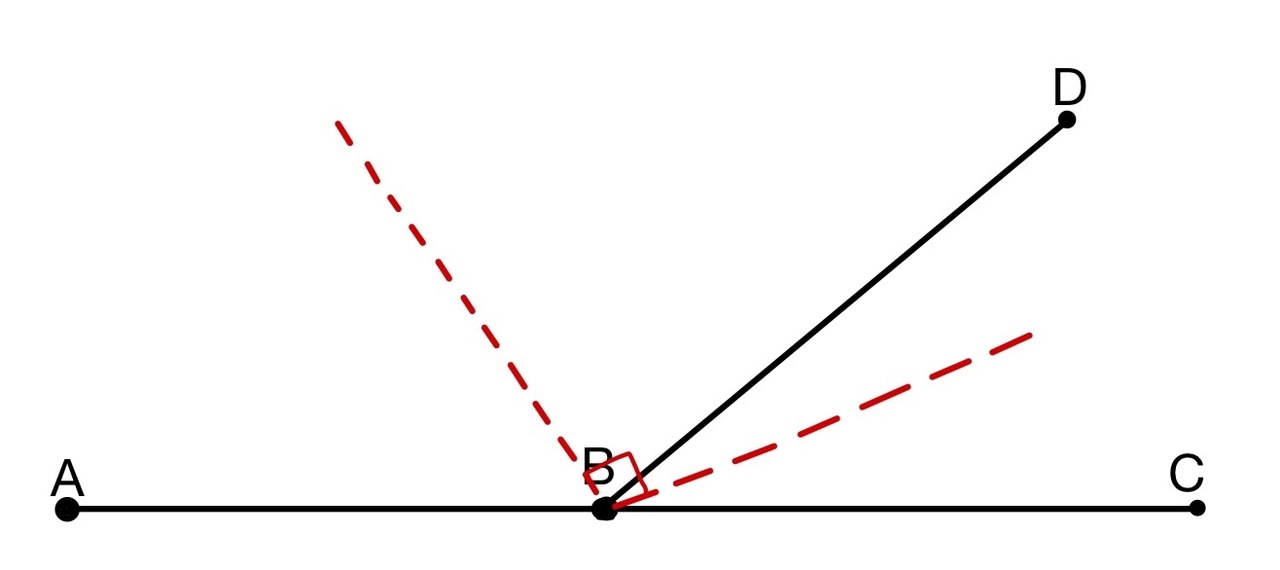
Найдите угол между биссектрисами двух смежных углов.
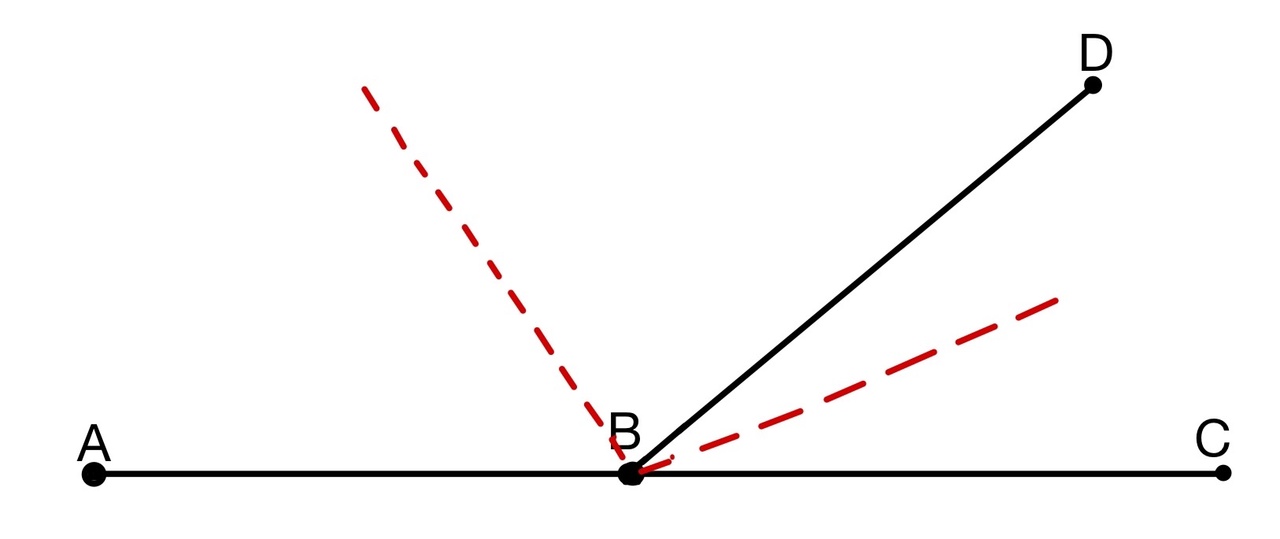
Источники:
Сумма смежных углов:
Биссектрисы делят углы пополам:
Ошибка.
Попробуйте повторить позже
Определите величину угла если известно, что он в
раза меньше смежного с ним угла.
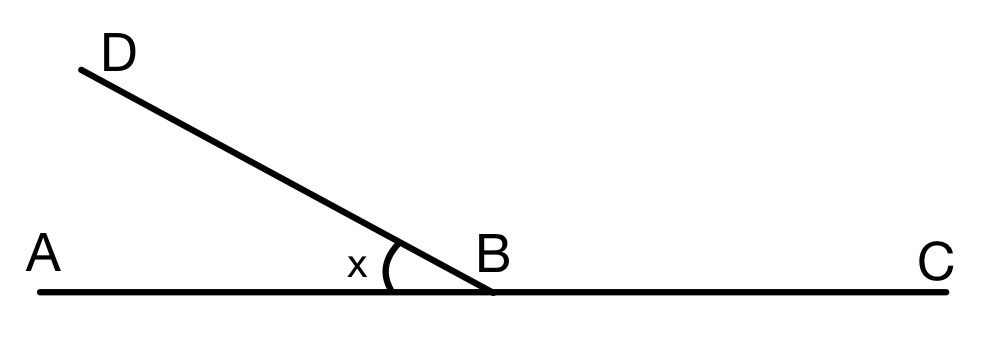
Источники:
Если неизвестный угол равен то смежный с ним равен
тогда по свойству смежных углов:
Ошибка.
Попробуйте повторить позже
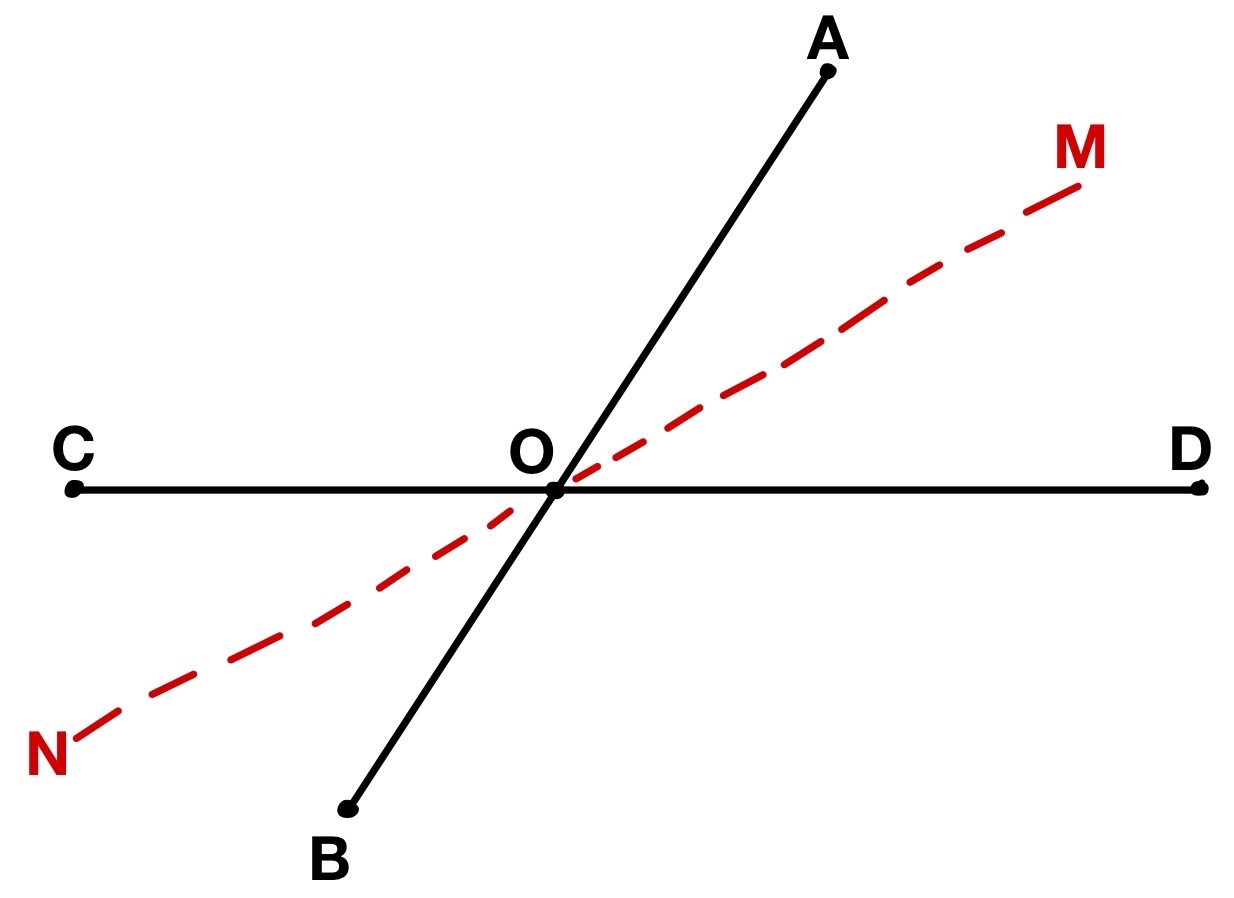
Чему равен угол между биссектрисами двух вертикальных углов и
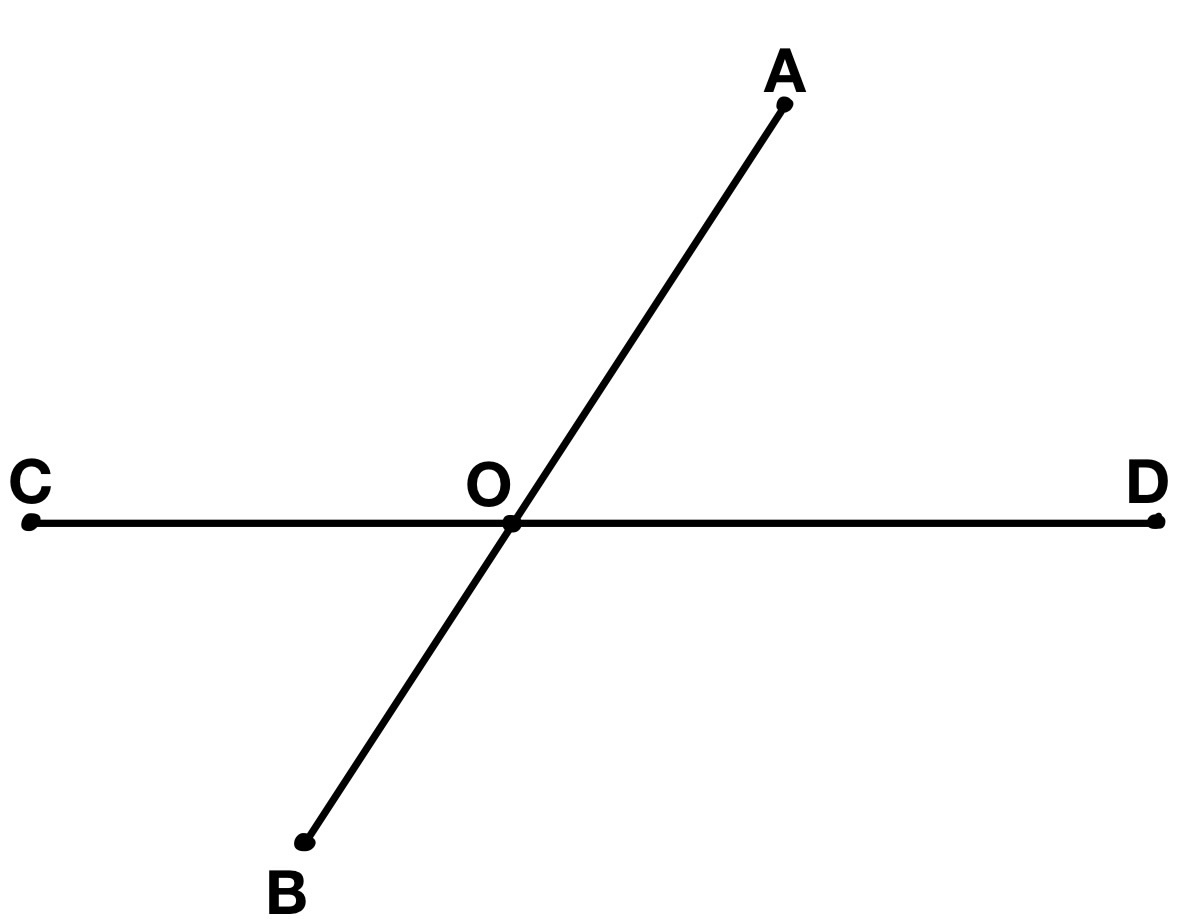
Источники:
Вертикальные углы равны:
Биссектрисы делят углы пополам:
Но угол между биссектрисами равен развернутому углу минус сумма половин углов:
Однако при пересечении биссектрис образуется угол:
Ошибка.
Попробуйте повторить позже
Найдите величину угла смежного с углом
если
Источники:
Сделаем чертёж по условию задачи:
.png)
По определению смежных углов:
Подставим известное значение:
Выразим и вычислим
Значит, угол смежный с углом
равен
Ошибка.
Попробуйте повторить позже
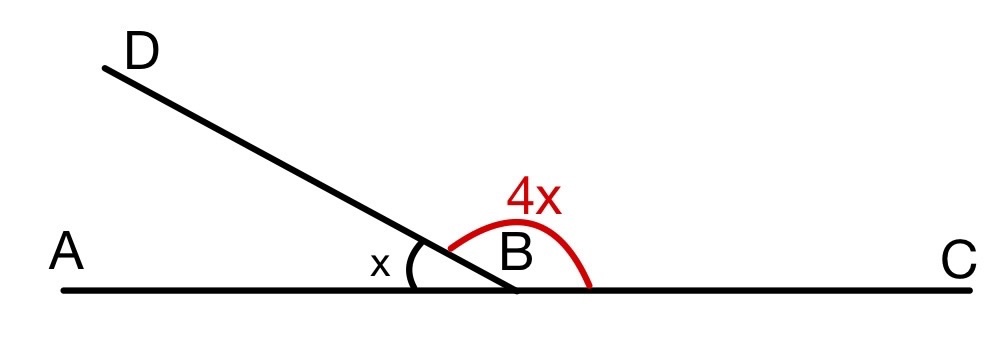
На рисунке 4 в 4 раза больше
Найдите все углы.
.png)
Источники:
Обозначим градусную меру угла за
Тогда
Так как эти углы смежные, их сумма равна
То
есть:
Значит,
Так как и
вертикальные, значит, они равны. То есть
Так как и
вертикальные, значит, они равны. То есть
Ошибка.
Попробуйте повторить позже
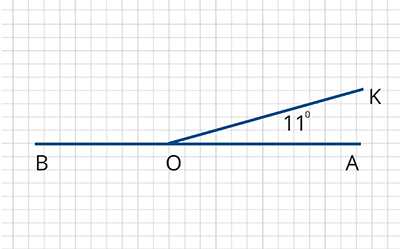
Используя чертёж, найдите угол (Рисунок, где развернутый угол
и луч
угол
Источники:
Воспользуемся свойством смежных углов: сумма смежных углов равна По условию задачи
Тогда:
Ошибка.
Попробуйте повторить позже
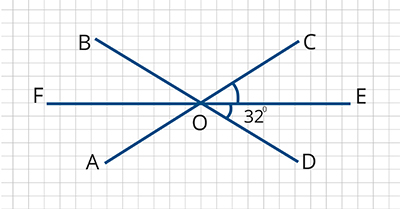
Используя чертёж, найдите угол
Варианты ответов:
- 1.
-
- 2.
-
- 3.
-
- 4.
-
Источники:
На чертеже указано, что углы Значит,
смежный с углом
по свойству смежных углов:
116
Ошибка.
Попробуйте повторить позже
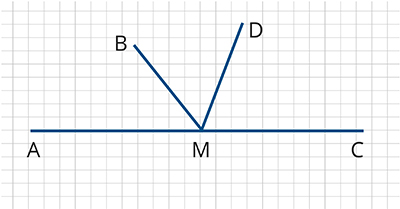
iИспользуя чертёж, найдите градусную меру угла если
Выберите верный ответ из списка:
- 1.
-
- 2.
-
- 3.
-
- 4.
-
Источники:
По чертежу можно увидеть, что является частью
и
Рассмотрим
и
Эти
углы – смежные, т.е. их сумма равна
Значит, зная градусную меру
мы сможем найти градусную меру
Теперь рассмотрим Мы знаем градусные меры
и
значит, мы сможем найти градусную
меру
Ошибка.
Попробуйте повторить позже
и
смежные.
в 5 раз больше
Чему равен
?
Источники:
Пусть Тогда
Так как
и
смежные, то их сумма равна
Следовательно,
Ошибка.
Попробуйте повторить позже
Градусные меры смежных углов пропорциональны числам и
Вычислите градусную меру большего угла.
Выберите верный ответ.
- 1.
-
- 2.
-
- 3.
-
- 4.
-
Источники:
Пусть коэффициентом пропорциональности будет Тогда градусные меры смежных углов равны
и
Сумма смежных углов равна
Составим уравнение:
Тогда градусная мера большего угла равна
Ошибка.
Попробуйте повторить позже
Используя чертёж, вычислите градусные меры углов и
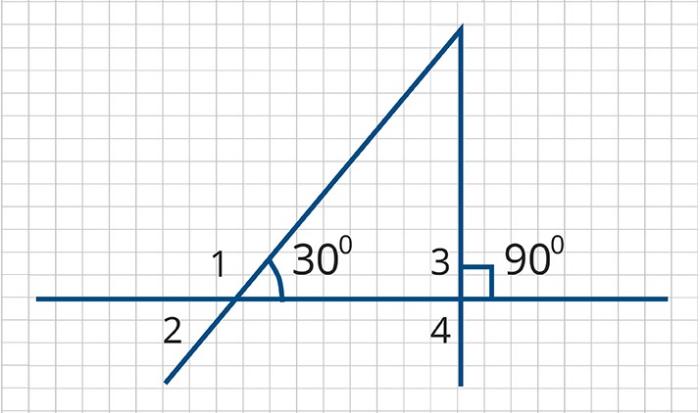
Источники:
и угол
смежные, поэтому:
вертикальный углу
- прямой угол в прямоугольном треугольнике:
и
смежные:
Ошибка.
Попробуйте повторить позже
Используя чертёж, найдите угол EOF.
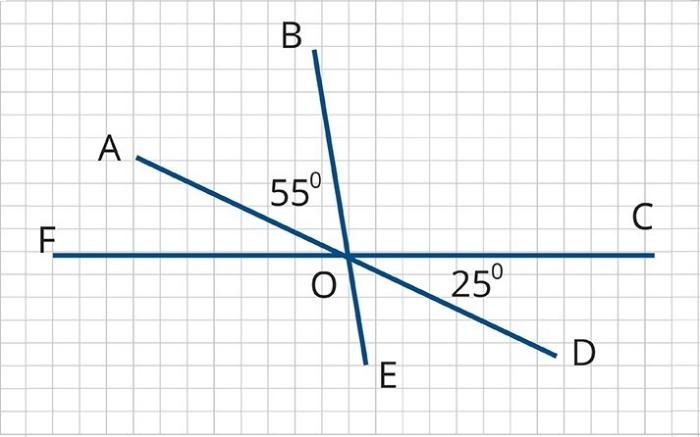
Источники:
- 1.
-
и
вертикальные, следовательно,
- 2.
-
Сумма смежных углов равна
- 3.
-
- 4.
-
- 5.
-
Поэтому
Ошибка.
Попробуйте повторить позже
Используя чертёж, найдите угол
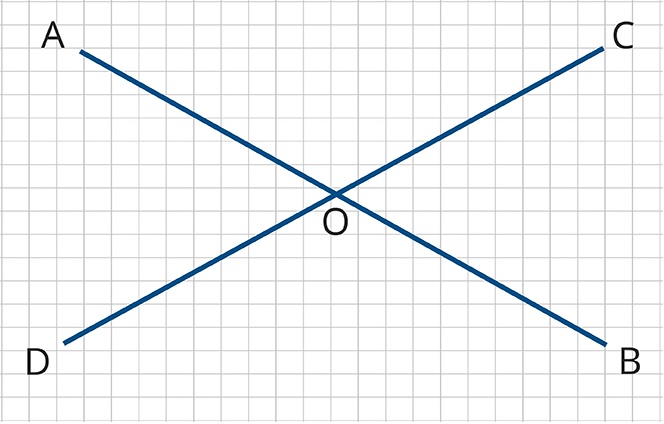
Источники:
Пусть
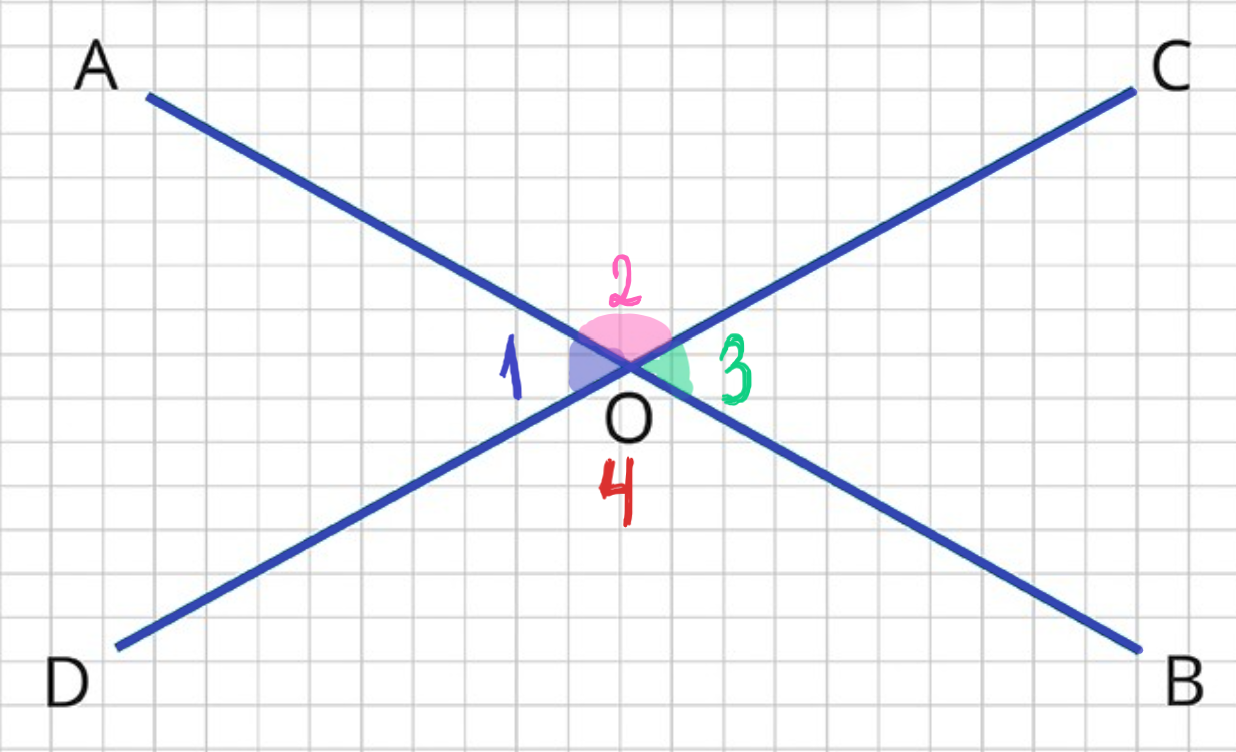
- 1.
-
и
смежные, поэтому
- 2.
-
и
смежные, поэтому
- 3.
-
Значит, если мы сложим все четыре угла, мы получим
- 4.
-
По условию,
То есть
- 5.
-
Тогда
- 6.
-
(как вертикальные углы).
- 7.
-
Значит,
- 8.
-
(как вертикальные углы).
- 9.
-
Вернемся к выражению из условия:
- 10.
-
- 11.
-
- 12.
-
Так как
(вертикальные углы), то
(то есть
) =



