Тема Формула единства - задания по годам

Формула единства 2020

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела формула единства - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#39873

На доске написано число $2$ . Двое играют в игру, делая ходы по очереди: каждый из игроков своим ходом может написать на доске любую степень двойки (то есть число вида $k 2 ,k ≥1$ ). Игрок, после хода которого на доске появятся две одинаковые цифры, проигрывает. У кого из игроков (у того, кто начинает, или у его соперника) есть способ выиграть при любой игре другого? Как он должен действовать?

Источники: ФЕ-2020, 8.4 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1!

Давайте посмотрим, какие цифры у степеней двойки мы знаем. Например, мы знаем, на что они всегда заканчиваются. Давайте попробуем это использовать

Подсказка 2!

2) Да-да, пытаемся сделать так, чтобы наш соперник не смог походить. То есть чтобы все цифры на конце степеней возможные уже были выписаны в числе.

Показать ответ и решение

Тот, кто начинает, может написать число $214 = 16384$ и победить, потому что любая степень двойки оканчивается на цифры $2,4,6,8$ , а все эти цифры уже будут написаны на доске.

Ответ:

У ходящего первым игрока. Он может написать число $16384$ .

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#73601

При каком наибольшем $n$ множество ${3,4,5,...n}$ можно так покрасить в синий и красный цвета, чтобы произведение двух любых (в том числе одинаковых) чисел одного цвета имело другой цвет?

Источники: ФЕ-2020, 11.5 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Попробуйте придумать число, которое вот вообще не получится нормально покрасить ни в один из цветов) Тогда сразу ясно что n меньше этого числа.

Подсказка 2

Удобнее всего строить это число на основе лишь одного простого числа - почти все делители его будут известны из цвета этого простого числа)

Подсказка 3

Докажите, что 243 вообще нельзя раскрасить. А дальше придумайте раскраску на n = 242. Удобнее всего раскрасить числа так, чтобы произведения были либо достаточно маленькие, либо уже очень большие)

Показать ответ и решение

Докажем, что число $35 = 243$ не может быть покрашено. Действительно, пусть $3,$ например, синее, тогда $9 =3⋅3$ красное, $81= 9⋅9$ синее, $243= 3⋅81$ красное. Заметим, что $27$ не может быть ни красным, ни синим: если $27$ красное, то в пример $27⋅9= 243$ входят три красных числа, а если $27$ синее, то в пример $27⋅3= 81$ входят три синих числа.

Пример. Числа от $3$ до $8$ покрасим синим, числа от $9$ до $80$ — красным, числа от $81$ до $242$ — снова синим.

Ответ:

$242$

Ошибка.
Попробуйте повторить позже

Задача 3#97439

В противоположных углах шахматной доски стоят Красная и Белая Королевы. Раз в минуту они случайным образом переходят на соседнюю по стороне клетку (одна только вправо или вверх, другая только влево или вниз). Какова вероятность, что они одновременно окажутся в одной клетке (и будут стоять там вместе в течение минуты)?

Источники: ФЕ - 2020, 11.3 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Обе королевы начинают в противоположных углах и движутся навстречу друг другу. Сколько ходов потребуется каждой, чтобы достичь центра доски? Как это связано с вероятностью встречи? Подумайте о симметрии)

Подсказка 2

Каждая королева может двигаться только в 2 направлениях. Сколько всего существует различных путей для каждой из них за 7 ходов? Как посчитать количество «совпадающих» траекторий?

Подсказка 3

Все возможные точки встречи лежат на центральной диагонали. Для каждой клетки на этой диагонали вычислите число путей обеих королев до неё. Как использовать биномиальные коэффициенты С для этого?

Подсказка 4

Общее число возможных траекторий для двух королев - 2¹⁴. Сколько из них приводят к встрече? Чтобы получить итоговую вероятность, осталось досчитать ручками)

Показать ответ и решение

Допустим, что королевы встретились в одной клетке. Заметим, что «расстояние в ходах королев» между противоположными углами равно $14,$ поэтому встретились королевы в момент, когда каждая совершила по $7$ ходов. Траектории двух королев, взятые вместе, образуют $14$ -звенную ломаную. Количество таких ломаных равно $7 C14$ (чтобы задать ломаную, надо выбрать, какие $7$ из $14$ звеньев вертикальны), и это и есть количество подходящих способов движения королев. Общее же количество способов движения за $7$ ходов равно $7 7 14 2 ⋅2 = 2 ,$ и они равновероятны (каждая королева в каждый момент выбирает одно из направлений движения; оба направления возможны, поскольку они ещё не упёрлись в край доски). Значит, искомая вероятность равна $7 14 11 C14 :2 = 429 :2 .$

______________________________________________________________________________________________________________________________________________________

Возможно и такое рассуждение, приводящее к другой форме ответа. Все клетки, удалённые от углов на равное число ходов (а именно на $7$ ходов), лежат на диагонали доски. Для каждой клетки диагонали найдём количество ситуаций, при которых обе королевы за $7$ ходов дошли до неё. Пусть $k$ — номер клетки на диагонали (от $0$ до $7),$ тогда число путей для любой из королев до этой клетки равно $Ck7$ (из $7$ ходов $k$ в одном направлении, остальные в другом). Столько же способов для другой королевы. Значит, всего есть $( )2 Ck7$ способов встретиться в этой клетке. Суммируя количество способов встретиться на каждой из клеток и деля на общее количество ситуаций, получаем вероятность $∑ ( ) 7k=0Ck72 :214.$

Ответ:

$-429 2048$

Ошибка.
Попробуйте повторить позже

Задача 4#123419

Прямоугольник $ABCD$ сложили вдоль линии $MN$ так, что точки $B$ и $D$ совпали. Оказалось, что $AD = AC′.$ Найдите соотношение сторон прямоугольника.

Источники: ФЕ - 2020, 11.1 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Обратите внимание на ключевые данные: после разлома AD = AC. Что это говорит о треугольниках ACD и ACD? Как связаны их стороны и углы? Рассмотрите симметрию относительно линии разлома MN.

Подсказка 2

Из симметрии следует, что CD = BC. Почему? Как это помогает найти углы в получившихся треугольниках?

Подсказка 3

Поаробуйте доказать, что треугольник ACD равносторонний. Какие углы в нём равны 60°? Как это связано с прямоугольным треугольником AND?

Подсказка 4

В прямоугольном треугольнике AND с углом 30° катеты связаны как 3:1. Как это соотношение переносится на стороны исходного прямоугольника ABCD?

Показать ответ и решение

$PIC$

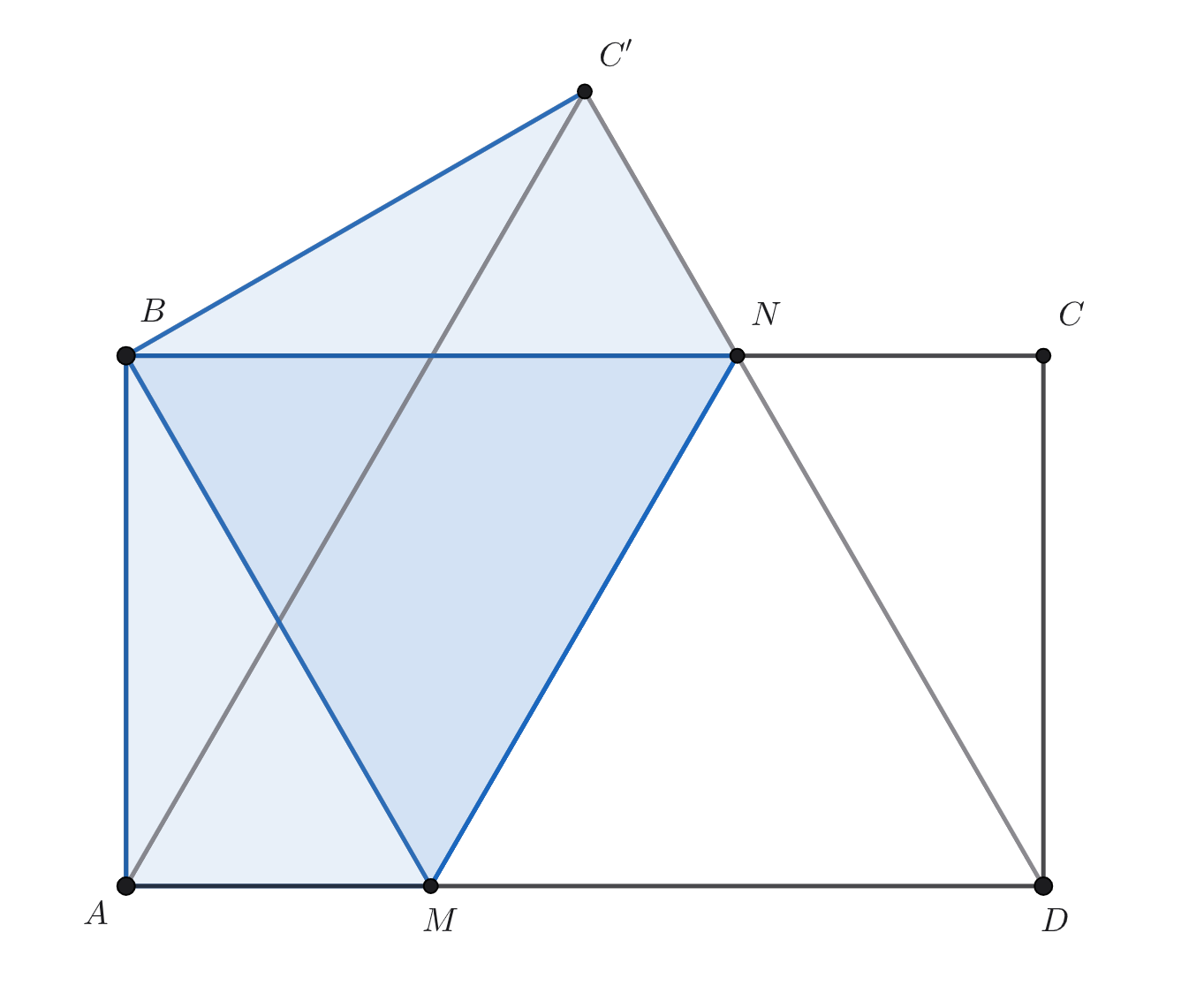
Из условия следует, что точка $B$ симметрична $D,$ а точка $C′$ симметрична $C$ относительно $MN.$ Значит, отрезок $C′D$ симметричен отрезку $BC$ относительно $MN,$ поэтому $C′D = BC.$ Кроме этого, точка $N$ при симметрии переходит в себя, поэтому развёрнутый угол $BNC$ переходит в угол $C ′ND,$ который, следовательно, тоже развёрнутый. Получается, точка $N$ лежит на прямой $C ′D.$

Противоположные стороны прямоугольника равны, поэтому $AD = BC = C′D.$ По условию $AD = AC′.$ Отсюда, $AC′ = AD = C′D,$ то есть треугольник $AC′D$ равносторонний и $∠C ′DA = 60∘.$ Так как $N ∈ C′D,$ то:

∠NDC = ∠C′DC =90∘− 60∘ =30∘

Получается, $△NDC$ — прямоугольний треугольник с углом $30∘.$ По свойству таких треугольников:

√- NC = 1ND, CD = -3ND 2 2

В силу симметрии $BN = ND,$ откуда

BC = BN +NC =ND + NC = ND + 1ND = 3ND 2 2

Итак, соотношение сторон прямоугольника равно

3 BC-= √2ND--= √3 CD --3ND 2

Ответ:

$√3$

Ошибка.
Попробуйте повторить позже

Задача 5#123420

Юлианский календарь устроен так: каждый год с номером, кратным $4$ — високосный; в обычном году $365$ дней, а в високосном — на $1$ больше; кроме этого, есть семидневная неделя. В результате существуют $14$ видов года: невисокосный год, начинающийся в понедельник, во вторник, . . ., в воскресенье; високосный год, начинающийся в понедельник, во вторник, . . ., в воскресенье.

Когда земляне поселились на планете Ялмез, то ввели календарь, в котором каждый год с номером, кратным $v(v > 1)$ — високосный; в обычном году $x$ дней, а в високосном — на $1$ больше; неделя по-прежнему состоит из $7$ дней. Оказалось, что в таком календаре ровно $n$ видов года. Найдите все возможные значения $n.$

Источники: ФЕ - 2020, 11.2 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Сосредоточьтесь на остатках при делении длины года на 7. Обычный год дает остаток х, високосный — х+1. Как это влияет на день начала следующего года? Есть ощущение, что именно остаток определяет, на какой день недели сдвинется начало следующего года

Подсказка 2

Рассмотрите полный цикл из v лет. Суммарный сдвиг составит vx+1 дней. Что происходит, когда это число кратно 7? А когда не кратно?

Подсказка 3

Если сдвиг не кратен 7, за v лет пройдут все возможные варианты начала года. Как это влияет на общее количество типов годов?

Показать ответ и решение

Лемма. Если $a$ не кратно $7,$ то среди чисел

m,m + a,m + 2a,...,m +6a

встречаются числа со всеми остатками от деления на $7.$

Если это не так, то какие-то два из семи остатков совпадают, но разность между соответствующими числами равна $ka,$ где $0< k< 7,$ а $a$ взаимно просто с $7,$ то есть не кратна $7.)$

Заметим, что нас интересует не сама длина года, а только её остаток от деления на $7,$ который далее и будем обозначать (для обычного года) $x.$ Ежегодно номер начального дня недели сдвигается на $x$ для обычного года и на $x +1$ для високосного. Например, если на планете Земля $2019$ год обычный и начинался во вторник, т. е. в день $2,$ то $2020$ год начинается в день $2+ 1= 3$ (где $1$ — остаток от деления $365$ на $7),$ а $2021$ — в день $3+2 =5$ (где $2$ — остаток от деления $366$ на $7).$

Тогда за $v$ лет номер начального дня сдвигается на $vx +1$ (например, для Земли на $5$ ). Если $vx +1$ не кратно $7,$ то встречаются все $7$ типов високосных лет (см. лемму); но тогда все годы перед ними («предвисокосные») тоже различаются, итого имеем все $14$ типов лет. Если $vx+1$ кратно $7,$ то последовательные високосные годы всё время одинаковы. Примеры (указаны длины лет по модулю $7):$

$pict$

Получить ровно $7$ типов лет невозможно: если в цикле $6$ обычных лет и один високосный (то есть $v =7),$ то число дней в цикле $6x+ (x+1)$ не кратно $7;$ если в цикле больше $6$ обычных лет и длина каждого из них не кратна $7,$ то все $7$ типов обычных лет встречаются; если длина бычного года кратна $7,$ то длина цикла не кратна $7.$

Ответ:

$2,3,4,5,6,8,14$

Ошибка.
Попробуйте повторить позже

Задача 6#123421

Каждая из двух сестёр загадала натуральное число от $1$ до $1000.$ Папа по очереди задаёт сёстрам (то одной, то другой) вопросы, на которые можно ответить «да» или «нет». Он хочет, задав не более чем по $6$ вопросов каждой из сестёр, выяснить, верно ли, что загаданные числа различаются более чем на $500.$ При этом ни одна из девочек не знает, что загадала другая, поэтому каждую сестру можно спрашивать только о её числе. Придумайте, как папе добиться цели.

Источники: ФЕ - 2020, 11.4 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Сначала определите, в каком интервале находится число первой сестры. Задайте вопрос: «Твоё число > 500?». Если ДА -> проверяем b < a - 500. Если HЕT - проверяем b > а + 500. (1) Для а > 500: сравниваем х = а - 500 и у = b. (2) Для а < 500: сравниваем х = a + 500 и у = b Теперь задача свелась к сравнению x и у! Первая сестра знает х, вторая знает у, но не знают друг о друге.

Подсказка 2

Используйте бинарный поиск для сравнения х и у: (1) Начните с полного диапазона [1;1000] для у. (2) Задавайте вопросы вида «у > k?» (например, k=500, 250, 750). Назвав наш промежуток возможных варинтов отрезок [m;n] будем отсекать ровно половину варинтов, но как? Почему нам пригодится именно целая чать от (m+n)/2?

Подсказка 3

Пересчитываем все варианты. Последние 2 вопроса уточнят: Равны ли х и у (тогда |a - b| = 500), или одно число строго больше другого (тогда |a - b| > 500). Если х < у для а > 500 или х > у для а < 500, условие выполнено!

Показать доказательство

Пусть первая сестра загадала число $a,$ а вторая сестра — число $b.$ Нам нужно узнать, верно ли, что $|a − b|> 500.$ Мы не можем сравнить числа и просто раскрыть модуль, так как каждая из сестёр знает только своё число, поэтому рассмотрим, чему эквивалентно неравенство в зависимости от $a:$

1) Если $a$ больше пятисот, то $b$ должно быть меньше пятисот для того, чтобы неравенство выполнялось. То есть, если $a >500,$ то неравенство эквивалентно $a− b> 500,$ или же $a− 500> b.$ Таким образом, нам нужно сравнить два числа: $x= a− 500$ и $y =b,$ при этом первая сестра знает, чему равно $x,$ а вторая сестра знает, чему равно $y.$ Пусть множество всех возможных значений $x$ это множество $X,$ а множество всех возможных значений $y$ — это $Y.$ Сейчас $X = [1;500],Y =[1;1000].$ Тогда $X ∩Y = [1;500].$

2) Аналогично, если $a≤ 500,$ то неравенство эквивалентно $b− a >500,$ или же $a+500< b.$ То есть нам так же нужно сравнить два числа: $x = a+500$ и $y = b,$ при этом первая сестра знает, чему равно $x,$ а вторая сестра знает, чему равно $y.$ Пусть множество всех возможных значений $x$ это множество $X,$ а множество всех возможных значений $y$ — это $Y.$ Сейчас $X = [501;1000], Y = [1;1000].$ Тогда $X ∩Y = [501;1000].$

Итак, в обоих случаях у нас получилось, что нужно сравнить два числа $x$ и $y,$ причём одно из чисел известно первой сестре, а другое второй, а пересечение множеств возможных значений этих чисел состоит из пятисот элементов. Зададим первой сестре вопрос: «Верно ли, что $a >500?$ » После этого введем $x$ и $y$ согласно случаям, расписанным выше, и будем сравнивать эти числа по одному алгоритму.

С каждым шагом будет уменьшать пересечение множеств $X$ и $Y$ в два раза. Например, второй вопрос будет: «Верно ли, что $y >250?$ » или «Верно ли, что $y > 750?$ » в зависимости от ответа на первый вопрос. Если на каком-то шаге $X ∩Y = [m;n],$ то мы спрашиваем, верно ли, что $x$ (или $y,$ в зависимости от того, кому задаем вопрос) больше, чем $[ ] m-+-n . 2$ Таким образом, после второго вопроса в пересечении множеств будет $X$ и $Y$ будет 250 элементов, после третьего вопроса — 175 элементов, после четвёртого — 88, и так далее. Получается, после десятого вопроса в пересечении будет всего один элемент. Пусть это будет число $z.$

При этом, после каждого вопроса уменьшается так же количество элементов в $X$ или в $Y.$ Пусть после десятого вопроса $X = [x1;z],Y =[z;y1]$ (или наоборот, все элементы множества $X$ не меньше $z,$ а все элементы множества $Y$ — небольше). Последние два вопроса будут: «Верно ли, что $x =z$ » или «Верно ли, что $y = z?$ ». Если ответы на оба вопроса «да», то числа $x$ и $y$ равны, и загаданные сёстрами числа различаются ровно на 500. Если ответ на первый из этих вопросов «нет», то $x< z ≤ y.$ Аналогично, если ответ на второй вопрос «нет».