Закл 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Дано натуральное число Натуральные числа
выписывают на доске в строчку в некотором порядке. У каждых двух стоящих
рядом чисел вычисляют их НОД (наибольший общий делитель) и записывают этот НОД на листке. Какое наибольшее количество
различных чисел может быть среди всех
выписанных на листке чисел?
Источники:
Подсказка 1:
Давайте начнем с оценки. Вот если есть два различных числа a, b и их НОД равен d, можно ли как-то оценить эти числа, используя d? И как, используя эти оценки, оценить сверху d некоторым выражением от n?
Подсказка 2:
Одна из самых очевидных оценок: min(a, b) ≥ d, max(a, b) ≥ 2d. Отсюда следует, что n ≥ 2d, откуда d ≤ [n / 2]. Осталось привести пример.
Подсказка 3:
Чтобы найти расстановку, для которой любое число d ≤ [n / 2] будет выписано, можно сделать так, чтобы числа вида d и 2d стояли рядом.
Подсказка 4:
Тут на помощь могут прийти числовые цепочки вида a, 2a, 2²a, ... Подумайте, почему они могут быть полезны, и как реализовать расстановку с ними?
Оценка. Предположим, что какое-то из выписанных на листке чисел больше скажем,
Тогда наибольшее из
чисел
не меньше
что больше
– противоречие (НОД двух чисел, не превосходящих
не превосходит
). Значит,
каждый из написанных
ов не превосходит
потому количество различных
ов не может превышать
Пример. Разобьём все числа от до
на цепочки вида
где
— нечётное число, не превосходящее
Выпишем
в строчку цепочки одну за другой. Тогда для любого натурального
найдётся цепочка, в которой встречается
а следующее за
число будет
Видим, что каждое натуральное
будет выписано на листке.
Ошибка.
Попробуйте повторить позже
На доску выписали 777 попарно различных комплексных чисел. Оказалось, что можно ровно 760 способами выбрать два числа и
записанных на доске, так, чтобы выполнялось равенство
Способы, которые отличаются перестановкой чисел, считаются одинаковыми. Докажите, что можно выбрать такие два числа и
записанных на доске, что
Источники:
Подсказка 1:
Для начала стоит переписать условие в более удобном виде. На что может намекать сумма квадратов и удвоенное произведение по разные стороны от знака равенства?
Подсказка 2:
Верно! На квадрат разности. Имеем (a − b)² = −1, то есть a − b = ±i. Аналогично преобразуем выражение, которое нужно доказать: (с − d)² = −45. Итого, нужно найти пару с разницей 45i. Что это означает?
Подсказка 3:
Нужно найти 46 "подряд идущих" чисел с разницей в i. Формально, мы хотим найти числа a₁, a₂, ..., a₄₆ с разницей ровно i между соседними. Тогда a₁ и a₄₆ будут являться искомой парой. В подобных задачах бывает полезно ввести граф.
Подсказка 4:
Разумеется, вершины — числа, ребро проводим, если разница между числами равна i. Хотим найти путь длины 46. Какие замечания можно сделать про этот граф?
Подсказка 5:
Осознайте, что в нём нет циклов, а также степень каждой вершины не более двух. Что же это означает?
Подсказка 6:
Граф представляет собой набор непересекающихся простых путей (так называемых бамбуков). Докажите это самостоятельно. Каждый такой путь — отдельная компонента связности, являющаяся деревом. Вершин в графе 777, рёбер — 760. Какой вывод из этих фактов можно сделать?
Подсказка 7:
В графе ровно 17 компонент связности (докажите это), то есть 17 путей, общая длина которых 760. Дело за малым — докажите, что путь длины хотя бы 45 найдется. Успехов!
Заметим, что условие равносильно тому, что
или же Рассмотрим граф, вершины которого — записанные на доску числа, а ребро проводится между двумя числами,
которые отличаются на
Согласно условию задачи, в таком графе ровно 760 рёбер. Каждая компонента связности этого
графа представляет собой путь и состоит из вершин-чисел вида
…,
Предположим, что в
этом графе
компонент связности. Тогда в нём
рёбер, поэтому
Поскольку
то в
какой-то компоненте связности хотя бы 46 вершин, поэтому какие-то две из этих вершин — это числа
и
Тогда
следовательно,
что и требовалось.
Ошибка.
Попробуйте повторить позже
Дана прямая призма Известно, что треугольники
и
— остроугольные. Докажите, что
точки пересечения высот этих треугольников вместе с точкой пересечения медиан треугольника
лежат на одной
сфере.
Источники:
Обозначим через и
точки пересечения медиан и высот треугольника
а также отметим точку
так,
что
Пусть сфера построена на отрезке
как на диаметре. Поскольку прямая
перпендикулярна плоскости
то точка
лежит на
Покажем, что на сфере
лежит точка пересечения высот
треугольника
рассуждение для двух других
треугольников аналогично.
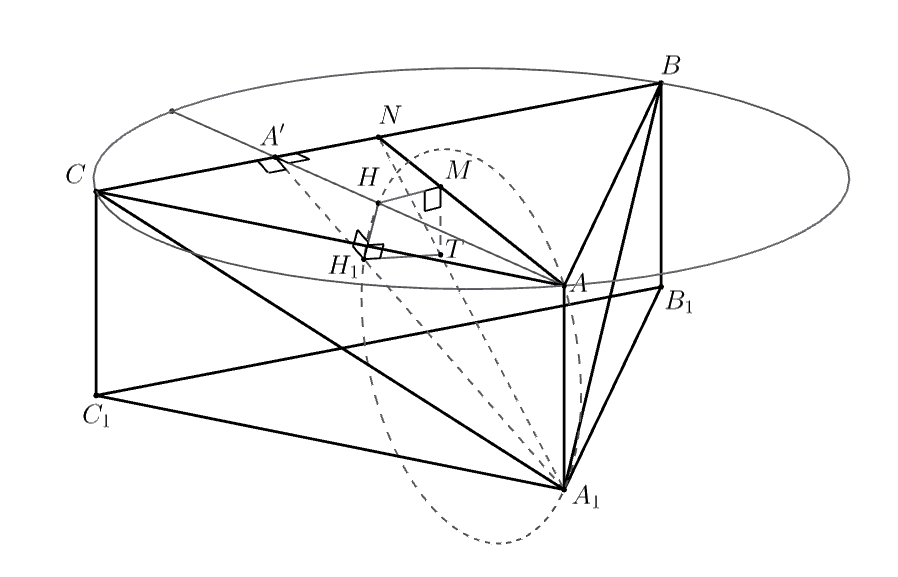
Обозначим через середину отрезка
Поскольку
точка
лежит на отрезке
в частности, она лежит в
плоскости
Пусть
— высота треугольника
Поскольку прямая
перпендикулярна плоскости
то
а также
по теореме о трёх перпендикулярах, то есть точка
лежит на отрезке
Поскольку точка, симметричная точке пересечения высот
треугольника
относительно прямой
лежит на его
описанной окружности, то
Применяя то же рассуждение для треугольника
мы получаем,
что
Следовательно, четырёхугольник вписанный, поэтому
Поскольку ещё
и
вновь применяя теорему о трёх перпендикулярах, мы получаем, что прямая
перпендикулярна плоскости
Значит,
то есть точка
лежит на сфере
что и требовалось.
Аналогично доказывается, что точки пересечения высот треугольников и
также лежат на сфере
Таким образом,
все пять точек (точки пересечения высот четырёх треугольников и точка пересечения медиан треугольника
) лежат на сфере
Ошибка.
Попробуйте повторить позже
Пару многочленов и
с целыми коэффициентами назовём важной, если из делимости на 100 обеих разностей
где — целые, следует, что числа
и
делятся на 100. Существует ли такая важная пара многочленов
и
что пара многочленов
и
тоже является важной?
Источники:
Подсказка 1:
Запишем в условие задачи в общем виде. У нас есть достаточное условие (А) для выполнения утверждения (В). Как вообще можно исследовать подобные конструкции? Например, подставить какой-то особенный набор в А, чтоб получить два утверждения В про него, которые либо наложат какие-то ограничения, либо приведут к противоречию. Разумеется, нас интересуют только остатки чисел по модулю 100, поэтому дальнейшие рассуждения ведутся в F₁₀₀. Подумайте, какие наборы было бы полезно подставить.
Подсказка 2:
Обратим внимание на то, что условие А зависит от функций, а утверждение В про их аргументы. Осознаем следующий факт: если аргументы одинаковые, то значения функций одинаковые, а вот наоборот работает не всегда. Благодаря этому мы можем провернуть один трюк. В условие А закинуть наборы функций, одинаковые по значению, но с разными аргументами. Тогда мы получим делимость на 100 для ненулевых разниц, а это уже продвижение. Заметьте, если бы было наоборот (условие А зависит от аргументов, а утверждение B про функции), то такой трюк бы не сработал. Теперь нужно понять, как именно осуществить предложенное.
Подсказка 3:
Начнём вводить обозначения в лоб. Пусть есть два набора (a ≥ b) и (c ≥ d) такие, что F(a, b) = F(c, d), G(a, b) = G(c, d). Тогда из условия А получаем, что a − c и b − d делятся на 100. Всё бы ничего, если a − c, b − d > 99. Такое вполне может быть. Но мы же хотим получить дополнительные ограничения...
Подсказка 4:
Значит, нужно ограничить a, b, c, d так, что a − c, b − d < 100. Какой самый простой способ это сделать?
Подсказка 5:
Просто взять a, b, c, d ≤ 99. То есть при этих ограничениях мы знаем, что если F(a, b) = F(c, d), G(a, b) = G(c, d), то (a, b) = (c, d). Отлично, давайте запишем теперь это построже и более масштабно.
Подсказка 6:
Рассмотрим всевозможные пары (a, b), где a, b ∈ F₁₀₀. Для каждой пары рассмотрим пару O(a, b) = [F(a, b), G(a, b)]. Мы поняли, что O(a, b) различны для различных пар (a, b). Но и пары (a, b) и пары O(a, b) — это просто комбинации остатков (mod 100). Что это значит?
Подсказка 7:
Что все пары O(a, b) — всевозможные пары остатков, причём каждая пара встречается один раз. Вернёмся к тому, о чём спрашивают в задаче. Если многочлены P(x, y) − xy и Q(x, y) + xy являются важной парой, то для них должно выполняться то же условие, что мы получили. Пока что не особо понятно, какой всё-таки ответ. В таких случаях нужно попробовать сначала доказать, что не существует, а если не получится это доказать (или хотя бы что-то нащупать), то уже пробовать строить пример. Итак, попробуем доказать, что не существует.
Подсказка 8:
Пусть для удобства теперь F(x, y) = P(x, y) − xy, G(x, y) = Q(x, y) + xy. O(x, y) = [F(x, y), G(x, y)], R(x, y) = [P(x, y), Q(x, y)]. Предположим, что F(x, y), G(x, y) — важные. Знаем, что набор {O(x, y), x, y ∈ F₁₀₀} = {R(x, y), x, y ∈ F₁₀₀} = {(x, y), x, y ∈ F₁₀₀}. Хотим найти противоречие. Доказывать, что какой-то пары остатков в {O(x, y)} нет — гиблый номер, ибо мы для этого ничего не знаем. Значит, нужно действовать хитрее и посмотреть на эти пары с другой точки зрения.
Подсказка 9:
Вся задача крутится вокруг модульной арифметики. Не будем же нарушать тенденции. Поскольку в {R(x, y)} есть всевозможные пары остатков, то там есть всевозможные пары с точки зрения чётности. Какой вывод из этого можно сделать?
Подсказка 10:
Осознайте, что если рассмотреть R(Ч, Н), R(Н, Ч), R(Ч, Ч), R(Н, Н) то мы получим перестановку набора (Н, Ч), (Ч, Н), (Н, Н), (Ч, Ч), где Ч, Н — произвольное чётное число и нечётное соответственно. Значит, для O(x, y) должно выполняться то же самое свойство. Но так ли это?
Подсказка 11:
Осталось просто разобрать случаи и осознать, что вот в этом и кроется проблема. У вас всё получится!
Пусть пара многочленов и
— важная. Рассмотрим пары остатков от деления на 100 чисел
и
где
—
всевозможные пары целых чисел от 0 до 99. Согласно условию задачи, все такие пары остатков разные. Поскольку всего пар чисел
то каждая пара остатков от деления на 100 достигается ровно один раз. Значит, достигаются все 4 возможные пары чётностей чисел
Поскольку чётность значения многочлена с целыми коэффициентами в точке
зависит только от чётности чисел
и
мы получаем, что пары значений
дают все четыре возможные пары чётностей. Однако заметим, что для пар многочленов и
первые три пары чётностей одинаковые, а последняя пара — разная. Следовательно, обе такие пары многочленов важными быть не могут.
не существует
Ошибка.
Попробуйте повторить позже
Дано натуральное число Куб со стороной
сложен из
единичных кубиков, каждый из которых — либо чёрный, либо
белый. Оказалось, что среди любых 8 кубиков, имеющих общую вершину и образующих куб
не более 4 чёрных кубиков. Какое
наибольшее количество чёрных кубиков могло быть использовано?
Источники:
Подсказка 1:
В подобных задачах всегда стоит поизучать примеры раскрасок, то есть не сразу делать оценку, а попробовать понять, как может выглядеть пример, заметить закономерности и так далее. Также частенько бывает очень полезно рассмотреть маленькие случаи, времени это много не займёт, а понимания может привнести достаточно. Итак, с чего начнём?
Подсказка 2:
Раз куб со стороной 2N + 1, то логичнее всего начать рассматривать случай куба 3×3×3. Исследуйте возможные примеры, удовлетворяющие условию.
Подсказка 3:
Уверены, пример на 18 вы построили, подумайте ещё и осознайте, что пример на 20 тоже строится несильно сложно. Теперь стоит подумать насчёт оценки...
Подсказка 4:
Она здесь тривиальная, рассмотрим два диагонально противоположных куба 3×3×3 и вот уже оценка на ≤ 20 готова (осознайте это). Итого, мы поняли, что для этого куба ответ 20. В такие моменты бывает очень полезно изучить число 20, а тем более то, как оно зависит от N (в нашем случае N = 1).
Подсказка 5:
20 = 2 * 2 * 5 = (N + 1)²(4N + 1) = 4N²(4N + 1) = 20N = 4N²(N+4) = ... (в случае N = 1). Также понятно, что ответ около трети от (2N+1)³. Очевидно, что в общем виде это многочлен с коэффициентом 4 при N³. Также естественное желание свести константы к минимуму (ну или оставить ± единички). На что это намекает?
Подсказка 6:
На то, что ответ, скорее всего, равен (N+1)²(4N + 1). Попробуем доказать эту гипотезу. С чего мы начнём?
Подсказка 7:
Разумеется, с примера, ведь подогнать пример под ответ проще, чем оценку (банально в силу наглядности). Итак, вперёд пробовать!
Подсказка 8:
Если вы достаточно попробовали, то, скорее всего, поняли, что совсем наглядно пример не строится (никакие красивые узоры не подходят), значит, нужно прибегать к аналитическому подходу...
Подсказка 9:
А от подобных мыслей недалеко до декартовой системы координат. Введём же её так, что все вершины единичных кубиков будут иметь целые координаты от 0 до 2N + 1. Рассмотрим произвольный куб 2×2×2. Хотим как-то в зависимости от координат вершин его кубиков определять его цвет.
Подсказка 10:
Но наборов координат всего 27, а кубиков 8, не хотелось бы рассматривать все эти наборы координат, в идеале для каждого кубика оставить свою координату, а ещё круче, если они будут выбраны "одинаково".
Подсказка 11:
Попробуем выбрать "наконечник" куба 2×2×2, то есть в каждом маленьком кубике рассмотрим вершину, которая ближе всего к началу координат. Этот наконечник образует куб из 8 вершин. Как координаты этих вершин записываются в общем виде?
Подсказка 12:
(a, b, c); (a + 1, b, c); (a, b + 1, c); (a, b, c + 1); (a + 1, b + 1, c); (a + 1, b, c + 1); (a, b + 1, c + 1); (a + 1, b + 1, c + 1). С какой точки зрения мы можем посмотреть на эти числа, учитывая, что a, b, c — произвольные?
Подсказка 13:
С точки зрения чётности! И нам нужно покрасить ровно 4 кубика в чёрный цвет. Как же это сделать?
Подсказка 14:
Давайте сделаем так, чтобы кубики, у которых в выбранном наборе координат хотя бы 2 чётные, будут чёрными, а остальные — белыми. Осознайте, что это искомый пример. Путём несложных вычислений докажите, что всего чёрных кубиков при такой раскраске ровно (N+1)²(4N+1). Осталось подогнать оценку под пример, однако наш пример уже достаточно сложный и идейный, может попробовать как-то использовать его в оценке?
Подсказка 15:
Давайте вместо отдельной оценки попробуем доказать оптимальность нашего примера (осознайте, что эти идеи разные). Пусть в общем виде кубик тёмный, если в нашем примере он чёрный, и светлый — если в примере он белый (то есть кубик вполне может быть тёмным и светлым одновременно). Раз пример аналитический, то оценка, скорее всего, такая же. В примере мы используем идеи чётности и расстояний, и они отлично работают, может стоит вновь прибегнуть к ним? Давайте для каждой целочисленной точки в нашей ДСК (a, b, c) введём определение t-ранга. t-ранг — минимальное расстояние до грани куба, перпендикулярной соответствующей оси (разумеется, t ∈ {x, y, z}). Значения рангов — r_x, r_y, r_z. А просто рангом точки (a, b, c) — r будем называть min(r_x, r_y, r_z). Вспомним про наши идеи, что можно сделать дальше?
Подсказка 16:
Отметим все целочисленные точки с нечётным рангом. Для каждой такой точки посчитаем разницу количества чёрных кубиков и количества белых кубиков, смежных с этой точкой. Что можно сказать про эту разницу?
Подсказка 17:
Вспомним условие и поймём, что она неположительна. Значит, сумма ∑ этих разностей по всем отмеченным точками также неположительна. Понятно, что какой-то конкретный маленький кубик мы учли несколько раз в ∑. Что тогда полезно было бы сделать?
Подсказка 18:
Ввести обозначение для количества отмеченных вершин конкретного кубика. Назовём эту величину кратностью. Воспользуемся техникой двойного подсчёта. Как же теперь с помощью новых обозначений можно посчитать ∑?
Подсказка 19:
Разумеется, ∑ = сумма всех кратностей чёрных кубиков — сумма кратностей белых кубиков. Итого, опираясь на некоторую "интуицию", мы ввели много обозначений и что-то поняли про ∑. Кажется, пришло время вновь немного поисследовать, посмотреть случаи. Рассмотрим произвольный кубик 2×2×2, пусть ранги его центра — r_x, r_y, r_z. Для однозначности будем считать, что r_x ≤ r_y ≤ r_z. Разберём несколько случаев.
Подсказка 20:
1) r_x < ry;
2) r_x = r_y = 1/2 + d, где d — чётно;
3) r_x = r_y = 1/2 + d, где d — нечётно.
Аккуратно разберите каждый случай и осознайте, что кратности всех тёмных кубиков не больше 4, а всех светлых — не меньше 4 (именно тёмных и светлых, а не чёрных и белых). Отличное продвижение. Давайте теперь для удобства введём обозначения кратностей: s₁ ≤ s₂ ≤ ... ≤ s_{(2N+1)³} С учётом продвижения и построенного примера, что можно сказать про эти кратности?
Подсказка 21:
Что s₁ + ... + s_{(N+1)²(4N+1)} = s_{(N+1)²(4N+1)+1} + ... + s_{(2N+1)³}, так как в примере ∑ = 0. Фух, осталось совсем немного. Осталось красиво завершить оценку противоречием. Пусть в раскраске чёрных кубиков > (N+1)²(4N+1). Что тогда?
Подсказка 22:
0 ≥ ∑ > s₁ + ... + s_{(N+1)²(4N+1)} − s_{(N+1)²(4N+1)+1} − ... − s_{(2N+1)³} = 0. В этой цепочке неравенств есть одно упущение (осознайте какое и допишите его, не забудьте обосновать). В итоге мы получили, что 0 > 0, если кубиков > (N+1)²(4N+1). Кажется, это победа)
Положим Введём систему координат так, что все вершины единичных кубиков будут иметь целые координаты от 0
до
Начнём с примера, показывающего, что количество чёрных кубиков действительно может быть равно У каждого кубика рассмотрим
его вершину, ближайшую к началу координат (её координаты принимают значения от 0 до
). Пусть кубик чёрный, если хотя бы две
координаты этой вершины чётны, и белый иначе. Ясно, что тогда в любом кубе
будет ровно 4 чёрных и 4 белых кубика. При
этом количество чёрных кубиков, у которых все три соответствующих координаты чётны, равно
а количество
кубиков, у которых чётны ровно две координаты, равно
поэтому общее количество чёрных кубиков будет равно
Осталось доказать, что этот пример оптимальный. Пусть куб сложен из чёрных и белых кубиков так, что выполнены условия задачи. Назовём кубик тёмным или светлым, если он является соответственно чёрным или белым в приведённом выше примере.
Для каждой точки с координатами в большом кубе назовём её
- и
-рангом соответственно числа
Назовём рангом этой точки число Иначе говоря,
- или
-ранг точки — это расстояние от неё до ближайшей
грани большого куба, перпендикулярной соответствующей оси, а её ранг — это просто расстояние от неё до ближайшей грани большого
куба.
Отметим все вершины единичных кубиков с нечётными рангами. Для каждой отмеченной вершины рассмотрим разность количеств
чёрных и белых кубиков, сходящихся в этой вершине; поскольку все эти вершины являются центрами кубов эта разность
неположительна. Значит, и сумма
всех таких разностей неположительна.
Скажем, что кратность единичного кубика — это количество его отмеченных вершин (столько раз этот кубик учтён в ).
Тогда
равна разности суммы всех кратностей чёрных кубиков и суммы кратностей всех белых кубиков. Поэтому
нам достаточно доказать, что если такая разность неположительна, то количество чёрных кубиков
не превосходит
Пусть
и
— это
-,
- и
-ранги центра некоторого кубика; пусть для определённости
Тогда нетрудно
видеть, что
- если
то кратность этого кубика равна 4;
-
если
где
чётно, то кратность кубика меньше 4, и он тёмный;
-
если
где
нечётно, то кратность кубика больше 4, и он светлый.
Итак, кратности всех тёмных кубиков не больше 4, а всех светлых — не меньше 4.
Пусть теперь
— кратности всех кубиков, расположенные в неубывающем порядке. Из сказанного выше вытекает, что
поскольку в приведённом выше примере значение было равно 0.
Если теперь в рассматриваемой раскраске чёрных кубиков, то
поскольку Это противоречие показывает, что
что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
По кругу выписаны 100 единиц. Петя и Вася играют в игру, каждый делает по ходов. Петя каждым своим ходом выбирает 9
стоящих подряд чисел и уменьшает каждое из них на 2. Вася каждый своим ходом выбирает 10 стоящих подряд чисел
и увеличивает каждое из них на 1. Ребята ходят по очереди, начинает Петя. Докажите, что Вася сможет действовать
так, чтобы после каждого его хода среди 100 выписанных чисел было не менее пяти положительных, как бы ни играл
Петя.
Источники:
Подсказка 1:
Нам нужно гарантировать 5 положительных чисел в любой момент. Есть несколько способов доказывать подобные утверждения. Первый способ: для любого момента доказать, что эти 5 чисел где-то найдутся, то есть просто доказать их существование. Второй способ: построить некоторый алгоритм ходов за Васю, зафиксировав некоторые числа, и доказать, что в любой момент именно они будут подходить (ну либо какие-то из них). Что же нам выбрать?
Подсказка 2:
Предпочтительнее для нас второй способ. Объясню почему. Доказывать существование нужно через какие-то оценки, общие суммы и так далее. Но мы смотрим на числа в целом, а в целом ходы Пети гораздо сильнее уменьшают общую сумму, нежели ходы Васи, поэтому через много ходов с помощью общих сумм и оценок мы просто не сможем доказать существование положительных чисел. Итого хотим найти некоторый набор чисел, который нам будет подходить в каждый момент.
Подсказка 3:
Доказывать, что какое-то число будет всегда положительным — гиблый номер, ибо Петя может с лёгкостью этому помешать. Если с одним числом не получилось, стоит рассмотреть пару...
Подсказка 4:
Попробовать доказать, что в какой-то паре при заданной стратегии хотя бы одно число будет положительным, уже не кажется плохой идеей. Однако пару тоже можно взять не любую...
Подсказка 5:
Если между числами из пары будет менее 8 чисел, то вновь Петя может всё испортить, так как одним ходом может уменьшить оба числа. Что же с парой чисел, между которыми ровно 8 других?
Подсказка 6:
Петя задевает ровно одно число из пары, в то время как Вася может прибавлять 1 сразу к обоим. Что тогда можно сказать про общую сумму в паре?
Подсказка 7:
Вася может сделать так, чтобы она не уменьшалась. А изначально сумма в паре положительна. Кажется, стратегия за Васю напрашивается сама собой, осталось найти 5 нужных пар. Успехов!
Обозначим записанные по кругу числа
…,
Вася будет следить лишь за десятью числами, которые он разобьёт на пары:
…,
За один ход Петя может уменьшить не более, чем одно из этих 10 чисел. Если Петя
уменьшил одно из чисел пары
Вася в ответ добавит 1 к числам
…,
Если же Петя не уменьшил
ни одно из этих 10 чисел, Вася сделает любой разрешённый ход. Таким образом, после пары ходов Пети и Васи сумма
чисел в каждой из пяти Васиных пар не уменьшится. Поскольку изначально пять сумм в парах положительны, то после
каждого Васиного хода сумма в каждой из этих пяти пар будет положительной, поэтому в каждой из пар будет хотя бы
одно положительное число. Таким образом, после любого Васиного хода будет хотя бы 5 положительных чисел, что и
требовалось.
Ошибка.
Попробуйте повторить позже
Четырёхугольник в котором нет параллельных сторон, вписан в окружность
В треугольники
вписаны окружности
соответственно. Проведены общие внешние касательные к окружностям
и
и
и
и
не содержащие сторон четырёхугольника
Четырёхугольник, последовательные стороны которого лежат на
четырёх проведённых прямых (именно в таком порядке), вписан в окружность
Докажите, что прямые, соединяющие центры
окружностей
и
и
и
пересекаются в одной точке.
Источники:
Пусть, не умаляя общности, лучи и
пересекаются в точке
лучи
и
пересекаются в точке
Обозначим через
центр окружности
точки
определим аналогично.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Четырехугольник является прямоугольником, стороны которого параллельны биссектрисам внутренних углов
и
Доказательство. Докажем, что прямая параллельна биссектрисе внутреннего угла
Действительно, пусть и
— середины дуг
и
не содержащие остальные вершины четырехугольника,
соответственно. Тогда в силу леммы о трезубце
но прямая
является биссектрисой угла
поэтому
.png)
С другой стороны, углы между парами прямых и
равны полусуммам пар дуг
и
а значит,
равны, следовательно,
перпендикулярна биссектрисе угла
Аналогично,
параллельна последней.
.png)
Как известно, биссектрисы внутренних углов перпендикулярны, следовательно, четырехугольник
суть прямоугольник,
поскольку пары его противоположных стороны параллельны биссектрисам.
_________________________________________________________________________________________________________________________________________________________________________________
Перейдем к решению. Таким образом, в силу доказанной леммы точка пересечения прямых является центром
описанной окружности
прямоугольника, т.е. достаточно показать, что окружности
имеют общую радикальную
ось.
Обозначим четырёхугольник, образованный четырьмя касательными через (прямая
— общая внешняя касательная к
и
аналогично с тремя другими сторонами). Пусть прямая
пересекает прямую
в точке
Точки обозначим через
описанную окружность четырёхугольника
Тогда точка — радикальный центр окружностей
и
поскольку она лежит на двух их радикальных осях. Значит,
радикальная ось окружностей
и
проходит через точку
аналогично, на ней лежат и точки
В частности, эти 4
точки лежат на одной прямой.
.png)
Пусть прямая пересекает сторону
в точке
и сторону
в точке
Поскольку
то
поэтому четырёхугольник
— вписанный. Поскольку
и
то по теореме
Фалеса
Из этого равенства отношений и вписанности мы получаем, что
то есть степень точки относительно окружностей
и
одинакова. Рассуждение для точек
аналогично. Итого
доказано требуемое утверждение.
.png)
Ошибка.
Попробуйте повторить позже
Пусть — непрерывная функция. Хордой будем называть отрезок целой длины, параллельный оси абсцисс, концы которого лежат
на графике функции
Известно, что у графика функции
ровно
хорд, причём среди них есть хорда длины 2025. Найдите
наименьшее возможное значение
Источники:
Для натурального положим
Тогда число хорд длины
равно количеству нулей функции
В качестве примера выберем следующую кусочно-линейную функцию :
при
и
при Заметим, что при
функция
принимает значение
только в точке
Следовательно, если
то обе точки
и
лежат в отрезке
В частности,
и нули функции
лежат в промежутке
Для
при
имеем
Значит,
имеет единственный нуль
то есть
хорда длины 2025 у функции
единственна. При натуральном
функция
монотонно убывает при
и
монотонно возрастает при
при этом
Таким образом, у этой
функции ровно два нуля, то есть функция
имеет по две хорды длины
Итого у неё 4049 различных
хорд.
Теперь перейдём к оценке. Без ограничения общности будем считать, что хорда длины 2025 соединяет точки и
то есть
Положим
Из условия следует, что у функции конечное число нулей, а также эта функция непрерывна. Пусть все её нули лежат в промежутке
Тогда функция
знакопостоянна на лучах
и
При необходимости, заменив функцию
на
будем
считать, что
при
Предположим, что при
Заметим, что
поэтому при
и
при
Значит, функция
имеет нуль, то есть у функции
есть хорда
любой натуральной длины, что противоречит условию.
Таким образом, при
Значит,
при
и при
Далее мы докажем, что при натуральных
и
в сумме дающих 2025, функция
имеет хотя бы 4 хорды длин
и
Применяя это утверждение для каждой такой
пары, получим оценку. Иными словами, докажем, что у функций
и
при
суммарно хотя бы 4
нуля.
Предположим, что это не так. Тогда функция имеет не более одного нуля. Значит,
не может быть отрицательной.
Действительно, если
то по непрерывности и знакам при больших
функция имеет хотя бы два нуля, противоречие.
Итого причём равенство нулю достигается не более чем в одной точке. Покажем, что
для некоторого
Рассмотрим наименьшее натуральное
для которого
делится на 2025, и обозначим остатки
…,
от деления чисел
…,
по модулю 2025. Если
положим
если
положим
Рассмотрим
разности
Если то
и
если же
то
и
Если
то
В случае
получаем
поскольку
и
Таким
образом,
и одно из крайних слагаемых положительно. Значит, найдётся что возможно только при
и
Тогда для
получаем
Заметим, что
Поскольку то
и
в частности,
и
то есть
В случае
и
получаем
а также
при больших
Тогда у
есть нули на промежутках
то есть хотя бы 4 нуля.
Если то
так как у
не более одного нуля. Тогда
В этом случае у
есть
нули на
и
а также в точке
и ещё один нуль в точке
есть у
что даёт хотя бы 4 нуля. Случай
разбирается аналогично.
4049


