Тема Регион 10 класс

Регион 2023

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела регион 10 класс

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#131037Максимум баллов за задание: 7

Дан бумажный треугольник, длины сторон которого равны 5 см, 12 см и 13 см. Можно ли разрезать его на несколько (больше одного) многоугольников, у каждого из которых площадь (измеренная в $2 см$ ) численно равна периметру (измеренному в см)?

Источники: ВСОШ, РЭ, 2023, 9.2 и 10.2 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Проверьте для исходного треугольника: чему равна его площадь? А его периметр?

Подсказка 2

Можно ли хороший многоугольник разрезать на несколько меньших хороших многоугольников?

Подсказка 3

Предположим, мы разрезали фигуру на несколько хороших многоугольников. Чему равна сумма площадей всех этих кусков? А теперь подумайте о сумме периметров всех кусков.

Показать ответ и решение

Многоугольник, у которого площадь (измеренная в $см2$ ) численно равна периметру (измеренному в см), назовём хорошим.

Заметим, что исходный треугольник — хороший: он прямоугольный с катетами $5$ см и $12$ см, поэтому его площадь равна $30$ $2 см$ и численно совпадает с его периметром, равным

5+ 12+ 13 =30 см.

Если какой-то многоугольник П разбит на хорошие многоугольники, то площадь П, равная сумме площадей всех многоугольников разбиения, совпала бы численно с суммой периметров многоугольников разбиения. Но сумма этих периметров больше периметра П (на удвоенную сумму длин общих частей границ многоугольников разбиения). Получаем, что площадь П больше его периметра.

Значит, никакой хороший многоугольник, в том числе данный треугольник, нельзя разрезать на несколько (больше одного) хороших многоугольников.

Ответ:

нельзя

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#131042Максимум баллов за задание: 7

В таблице $6× 6$ изначально записаны нули. За одну операцию можно выбрать клетку и заменить число, стоящее в ней, на любое целое число. Можно ли за 8 операций получить таблицу, в которой все 12 сумм чисел в строках и столбцах будут различными положительными числами?

Источники: ВСОШ, РЭ, 2023, 10.1 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Условие задачи даёт довольно много свободы: можно заменять значения на любое целое число, при этом таблица достаточно маленькая. Есть ощущение, что существует пример, удовлетворяющий условию.

Подсказка 2:

Чтобы было проще придумать пример, попробуйте использовать как маленькие, так и большие числа, чтобы суммы в разных столбцах и строках сильно отличались.

Показать ответ и решение

Один из многих возможных примеров показан на рисунке.

$PIC$

Ответ:

можно

Ошибка.
Попробуйте повторить позже

Задача 3#131045Максимум баллов за задание: 7

В городе $N$ прошли $50$ городских олимпиад по разным предметам. В каждой из этих олимпиад участвовало ровно $30$ школьников, но не было двух олимпиад с одним и тем же составом участников. Известно, что для любых $30$ олимпиад найдется школьник, который участвовал во всех этих $30$ олимпиадах. Докажите, что найдется школьник, который участвовал во всех $50$ олимпиадах.

Источники: ВСОШ, РЭ, 2023, 10.3 и 11.3 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Попробуйте решить задачу от противного: предположите, что нет школьника, который участвовал во всех 50 олимпиадах.

Подсказка 2

Тогда полезно посмотреть на пересечения пар множеств участников. Какого минимального размера может быть пересечение двух олимпиад?

Подсказка 3

Если пересечение двух множеств слишком маленькое, то для каждого школьника из него можно найти третью олимпиаду, в которой этого школьника нет.

Подсказка 4

Теперь рассмотрите пересечение выбранных двух олимпиад и олимпиад, в которых не участвуют школьники из их пересечения.
Общее пересечение пусто. А сколько всего олимпиад мы рассмотрели?

Подсказка 5

Пересечение менее 30 олимпиад не может быть пустым, значит, пересечение любых двух олимпиад равно 29.

Подсказка 6

Если множества участников всех олимпиад отличаются
друг от друга максимум одним человеком, то как устроено множество всех олимпиадников?

Подсказка 7

Если есть множество из 31 школьника, то сколько различных 30-элементных подмножеств можно составить из него? Достаточно ли этого, чтобы покрыть все 50 олимпиад?

Показать доказательство

Предположим противное, и пусть в множестве всех школьников есть различные $30$ -элементные подмножества

A1,A2,...,A50

— множества участников каждой олимпиады такие, что пересечение любых 30 из них непусто, а пересечение всех — пусто.

Пусть среди множеств

A1,A2,...,A50

нашлись два множества $B$ и $C,$ имеющие $k≤ 28$ общих элементов

x1,x2,...,x . k

Для каждого элемента $xi$ среди множеств

A1,A2,...,A50

найдём подмножество $Di,$ не содержащее $xi,$ такое подмножество $Di$ найдётся, иначе $xi$ — общий элемент множеств

A1,A2,...,A50.

(Заметим, что среди подмножеств $Di$ могут быть совпадающие.)

Тогда пересечение не более $30$ подмножеств

B,C,D1,...,Dk

— пусто. Это противоречит нашему предположению (к данным подмножествам можно добавить еще несколько, чтобы стало 30 подмножеств, при таком добавлении пересечение остается пустым).

Значит, указанных двух множеств $B$ и $C$ не найдётся. Тогда пересечение любых двух из множеств

A1,A2,...,A50

содержит в точности $29$ элементов. Пусть

A1∩A2 = {y1,y2,...,y29},

так что

A1 ={z1,y1,y2,...,y29}, A2 = {z2,y1,y2,...,y29}.

Найдём подмножество (пусть, для определённости, это подмножество — $A3$ ), не содержащее $y1.$ Так как

|A ∩ A |=|A ∩ A |=29, 1 3 2 3

то $A3$ обязано содержать все элементы

z1,z2,y2,y3,...,y29.

Этих элементов $30$ (все они различны), поэтому

A3 ={z1,z2,y2,y3,...,y29}.

Рассмотрим любое подмножество $Ai$ из подмножеств $A4,...,A50.$ Предположим, что $Ai$ содержит элемент, лежащий вне $31$ -элементного множества

K = {z1,z2,y1,y2,...,y29} =A1 ∪A2∪ A3.

Тогда $Ai$ должно пересекаться с каждым из подмножеств $A1,A2,A3$ по одному и тому же $29$ -элементному подмножеству множества $K.$ Но

|A1∩A2 ∩A3|= 28,

значит, такого $29$ -элементного подмножества не существует — противоречие. Отсюда делаем вывод, что все множества $A1,A2,...,A50$ являются подмножествами множества $K.$ Но в множестве $K$ количество $30$ -элементных подмножеств равно $31< 50.$ Получаем противоречие, завершающее решение задачи.

Ошибка.
Попробуйте повторить позже

Задача 4#131048Максимум баллов за задание: 7

Даны натуральные числа $a,b,c$ такие, что $a >1,$ $b> c> 1,$ а число $abc+ 1$ делится на $ab− b+1.$ Докажите, что $b$ делится на $a.$

Источники: ВСОШ, РЭ, 2023, 10.4 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Попробуйте из условия делимости вычесть делитель из делимого, чтобы получить новый вид выражения.

Подсказка 2

(abc + 1) − (ab − b + 1) = b(ac − a + 1). Обратите внимание, что в разности появляется множитель b.

Подсказка 3

Заметьте, что число b и число ab − b + 1 взаимно просты. Какой из этого вывод можно сделать?

Подсказка 4

Тогда ac − a + 1 делится на ab − b + 1. Сравните их.

Подсказка 5

Если ac − a + 1 < 2(ab − b + 1), то правда ли, что ac − a + 1 = ab − b + 1?

Подсказка 6

Да, так как ab − b + 1 делит ac − a + 1. Что даёт равенство?

Подсказка 7

А если его преобразовать к виду b(a − 1) = a(b − 1), вспомните про делимость.

Показать доказательство

Из условия следует, что

(abc+ 1)− (ab− b+1)= abc− ab+ b= b(ac− a +1)

делится на $ab− b+1.$ Заметим, что $b$ и

ab− b+ 1= (a − 1)b+1

взаимно просты, отсюда получаем, что $ac− a+ 1$ делится на $ab− b+1.$

Далее замечаем, что

0< ac− a+ 1< 2(ab− b+ 1).

Действительно,

2(ab− b+ 1)= (2a− 2)b+ 2> (2a − 2)c+2 =ac+ (a− 2)c+ 2≥ac+ 2> ac− a +1.

Значит, делимость $ac− a +1$ на $ab− b+ 1$ возможна только в случае равенства

ac− a+1 =ab− b+ 1.

Имеем

a(c− 1)= ac− a =ab− b= (a − 1)b.

Видим, что $(a− 1)b$ делится на $a,$ но так как $a− 1$ и $a$ взаимно просты, отсюда следует, что $b$ делится на $a,$ что и требовалось доказать.

Ошибка.
Попробуйте повторить позже

Задача 5#131049Максимум баллов за задание: 7

В остроугольном треугольнике $ABC$ проведена высота $BD$ и отмечена точка пересечения высот $H.$ Серединный перпендикуляр к отрезку $HD$ пересекает окружность, описанную около треугольника $BCD,$ в точках $P$ и $Q.$ Докажите, что $∘ ∠AP B+ ∠AQB = 180.$

Источники: ВСОШ, РЭ, 2023, 10.5 (см. olympiads.mccme.ru)

Показать доказательство

Заметим, что $PQ ∥CD,$ так что $PQ$ — средняя линия прямоугольного треугольника $AHD.$ Значит, $PQ$ пересекает гипотенузу $AH$ в её середине $M,$ так что $MA = MD =MH.$

$PIC$

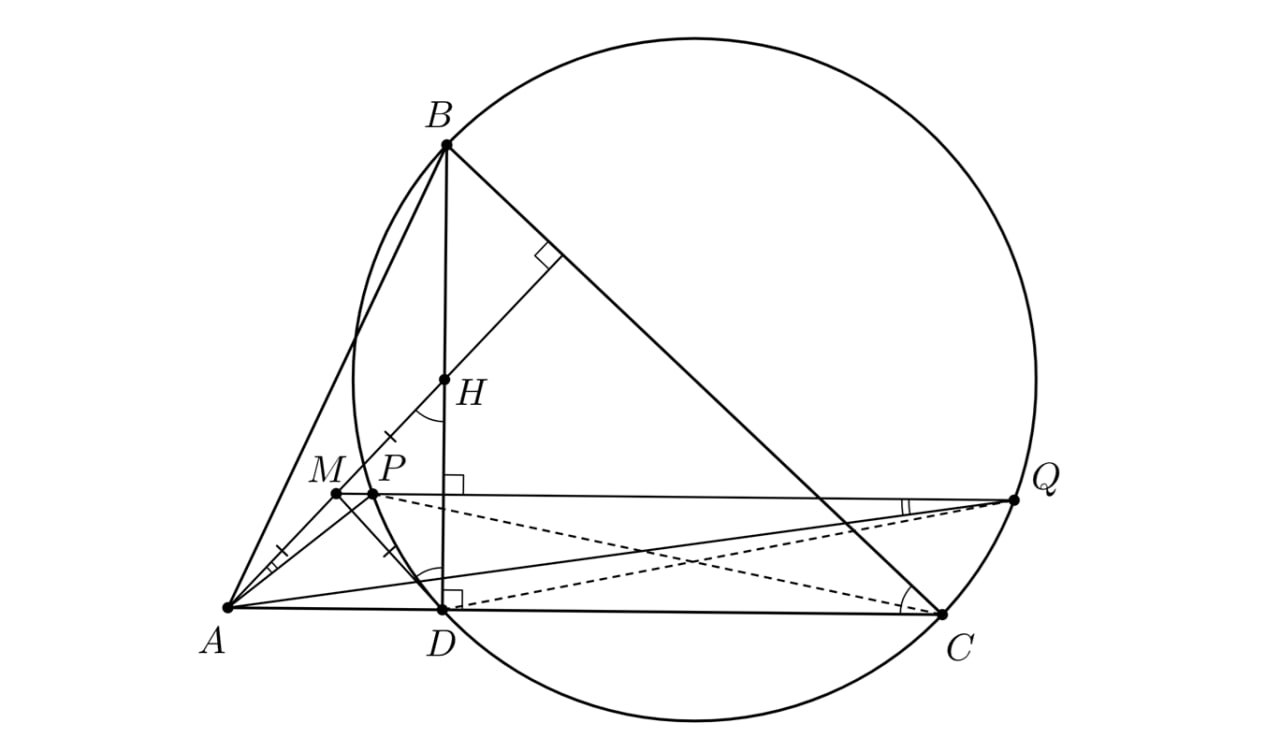
Имеем $∠MDH = ∠MHD,$ а поскольку $MH ⊥BC$ и $HD ⊥ CD,$ имеем также $∠MHD = ∠BCD.$ Получаем равенство $∠MDH = ∠BCD,$ из которого следует касание прямой $MD$ и окружности $(BCD )$ в точке $D.$ Отсюда $MD2 = MP ⋅MQ$ (по теореме о произведении отрезков секущей).

Далее, $MA2 = MP ⋅MQ.$ Значит, треугольники $AMP$ и $QMA$ подобны (угол $AMQ$ общий и $MA ∕MP =MQ ∕MA$ ). Отсюда $∠MQA = ∠MAP,$ поэтому

∠MP A +∠MQA = ∠MP A+ ∠MAP =∠HMQ = 90∘− ∠MHD =∠CBD.

Итак, $∠AP B +∠AQB = ∠CBD,$ и, поскольку

∠AP B +∠AQB =(∠MP A +∠MQA )+ (∠MP B+ ∠MQB ).

для завершения решения остаётся убедиться, что

∘ ∠MP B+ ∠MQB = 180 − ∠CBD.

Для определённости далее считаем, что $P$ лежит между $M$ и $Q.$ Имеем

∘ ∠MP B+ ∠MQB =180 − (∠BP Q− ∠MP Q).

Так как $PQ ∥CD,$ то дуги $PD$ и $CQ$ равны, а значит, опирающиеся на них вписанные углы равны. Тогда

∠BP Q − ∠P QB =∠BDQ − ∠P CB =(∠BDC − ∠QDC )− (∠DCB − ∠DCP )= ∠BDC − ∠DCB = ∠CBD,

что завершает доказательство.

Ошибка.
Попробуйте повторить позже

Задача 6#131382Максимум баллов за задание: 7

Петя взял некоторые трёхзначные натуральные числа $a ,a,...,a 0 1 9$ и написал на доске уравнение

9 8 2 a9x + a8x +...+a2x + a1x +a0 = ∗.

Докажите, что Вася сможет вместо звездочки написать некоторое 30-значное натуральное число так, чтобы получившееся уравнение имело целый корень.

Источники: ВСОШ, РЭ, 2023, 10.7 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Условие даёт слишком много свободы, существует множество трёхзначных и 30-значных чисел. Кажется, что пример существует.

Подсказка 2:

Есть два варианта, как можно придумать пример. Первый — придумать 30-значное число, для которого сразу найдется x, дающий это значение. Или же придумать x, дающий какое-то 30-значное число. Какой способ проще?

Подсказка 3:

Второй способ, разумеется, проще. Обратите внимание, многочлен состоит из 10 одночленов, а каждый коэффициент трёхзначный. Быть может, можно получить число, состоящее из коэффициентов, выписанных по очереди?

Показать доказательство

Пусть $x-yz- i ii$ — десятичная запись трехзначного числа $a i$ . Подстановка в левую часть уравнения $x =1000$ даёт

27 24 ------------- a9⋅10 +a8⋅10 +⋅⋅⋅+ a1⋅1000 +a0 = x9y9z9...x0y0z0.

Таким образом, после подстановки вместо звездочки $30$ -значного числа

----------------- x9y9z9x8y8z8...x0y0z0

получится уравнение, имеющее корень $1000.$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#131383Максимум баллов за задание: 7

Биссектриса угла $A$ параллелограмма $ABCD$ пересекает сторону $BC$ в точке $K.$ На стороне $AB$ выбрана точка $L$ так, что $AL = CK.$ Отрезки $AK$ и $CL$ пересекаются в точке $M.$ На продолжении отрезка $AD$ за точку $D$ отмечена точка $N.$ Известно, что четырёхугольник $ALMN$ — вписанный. Докажите, что $∘ ∠CNL = 90.$

Источники: ВСОШ, РЭ, 2023, 10.8 (см. olympiads.mccme.ru)

Показать доказательство

Первое решение. Поскольку $AM$ — биссектриса угла $LAN,$ отрезки $LM$ и $MN$ равны как хорды, стягивающие равные дуги. Теперь достаточно доказать, что $CM = LM$ (тогда $CM = LM =MN,$ значит, $CNL$ — прямоугольный треугольник, и $NM$ — его медиана, проведенная из прямого угла).

Так как

∠BKA = ∠NAK = ∠BAK,

треугольник $ABK$ — равнобедренный (симметричный относительно серединного перпендикуляра к $AK ).$ Отметим на стороне $BK$ точку $X$ так, что $LX ∥AK.$ Из симметрии треугольника $ABK$ имеем $KX = AL.$ Тогда имеем $KX = CK$ и $MK ∥ LX,$ значит, $MK$ — средняя линия треугольника $CLX,$ значит, $CM = LM,$ что завершает решение.

$PIC$

Второе решение. Пусть $∠BAD =2α.$ Заметим, что $DM$ — биссектриса угла $ADC.$ Действительно, продлим $AK$ до пересечения с $CD$ в точке $Y.$ Тогда, используя подобия $AML ∼ YMC$ и $AY D∼ KY C,$ имеем

AM--=-AL = CK-= AD-. MY Y C YC DY

Из полученного равенства $AM∕MY =AD ∕DY$ вытекает, что $DM$ — биссектриса треугольника $ADY.$ Отсюда

∠MDC = ∠ADC ∕2= (180∘− 2α)∕2= 90∘ − α.

$PIC$

Из вписанности $ALMN$ имеем $∠CMN = ∠LAD,$ а из параллельности $AB ∥ CD$ следует $∠LAD = ∠CDN.$ Поэтому $∠CMN = ∠CDN,$ значит, четырёхугольник $CMDN$ — вписанный. Отсюда

∘ ∠MNC = ∠MDC = 90 − α.

Из вписанности

∠LNM = ∠LAM = α.

Тогда

∠LNC = ∠MNC + ∠LNM = 90∘,

что и требовалось доказать.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. Отметим, что в решении 2 при доказательстве того, что $DM$ — биссектриса угла $ADC,$ не использовалось то, что $AM$ — биссектриса угла $A.$ А при доказательстве вписанности $CMDN$ не использовалось также равенство $AL = CK.$

Ошибка.
Попробуйте повторить позже

Задача 8#131384Максимум баллов за задание: 7

Дано натуральное число $k.$ Вдоль дороги стоят $n$ столбов через равные промежутки. Миша покрасил их в $k$ цветов и для каждой пары одноцветных столбов, между которыми нет других столбов того же цвета, вычислил расстояние между ними. Все эти расстояния оказались различны. При каком наибольшем $n$ так могло оказаться?

Источники: ВСОШ, РЭ, 2023, 10.9 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Для удобства расстояние между соседними столбами примем за единичное. Также пронумеруем их от 1 до n. Пусть nᵢ — количество столбов i-го цвета. Сколько всего будет искомых пар?

Подсказка 2:

Несложно догадаться, что для одного цвета таких пар nᵢ − 1 (количество промежутков). Значит, всего n₁ − 1 + ... + nₖ − 1 = n − k. Задача на оценку + пример, однако по условию нам дана только различность всех расстояний. Для примера, как мы можем оценить сумму 2-ух различных натуральных чисел, зная, что они от 1 до 5?

Подсказка 3:

Очевидно, что она ≥ 1 + 2 и ≤ 4 + 5. Применим аналогичную идею, только сумму чего будем оценивать?

Подсказка 4:

Кажется, хорошей идеей будет оценить сумму всех расстояний S. S ≥ 1 + 2 + ... + (n − k) = (n − k)(n − k − 1)/2. Да, мы получили какое-то неравенство, но оценку на количество из него пока что не вывести. Какое неравенство мы хотим получить для итоговой оценки?

Подсказка 5:

То, где с обеих сторон участвуют только переменные n и k. С правой частью мы справились, что же делать с левой?

Подсказка 6:

Необходимо выразить или оценить сверху S с помощью n и k (идея двойного подсчёта). Зайдём из далека. Как можно посчитать (не оценить) сумму расстояний для конкретного цвета?

Подсказка 7:

Попробуем сначала самым честным и пробивным способом. Пусть d₁, ..., dₚ — номера столбов первого цвета (НУО). Тогда искомая величина равна d₂ − d₁ + d₃ − d₂ + ... + dₚ − dₚ₋₁. А если покороче?

Подсказка 8:

Сумма расстояний для первого цвета = dₚ − d₁ (в целом, это интуитивно). Может обобщим эту идею?

Подсказка 9:

Пусть aᵢ — номер первого столбца i-го цвета, bᵢ — последнего. Тогда чему же равно S?

Подсказка 10:

S = b₁ − a₁ + ... + bₖ − aₖ = b₁ + ... + bₖ − (a₁ + ... + aₖ). Однако переменных k и n мы пока что не наблюдаем. Как бы их привязать к этому выражению?

Подсказка 11:

Разумеется, в явном виде выразить через n и k мы не сможем (ибо сумма может быть разной), значит, нужно вновь оценить сверху (чтоб нам на руку сыграла транзитивность в неравенствах). Посмотрим, что мы имеем: две суммы различных чисел. Кажется, мы где-то это уже видели...

Подсказка 12:

Поскольку мы хотим получить оценку сверху на S, то сумму b₁ + ... + bₖ нужно оценить снизу, а a₁ + ... + aₖ сверху. Метод нам известен, а что же получается в итоге?

Подсказка 13:

S ≤ k(n − k) (получите данный вид самостоятельно). Что же мы имеем? (n − k)(n − k − 1)/2 ≤ S ≤ k(n − k). Какая оценка на n у нас получилась?

Подсказка 14:

n ≤ 3k − 1. Осталось придумать пример. Он строится из оценки, всего лишь необходимо гарантировать равенства во всех выше написанных неравенствах. Успехов!

Показать ответ и решение

Пронумеруем столбы от 1 до $n$ вдоль дороги и примем за 1 расстояние между соседними столбами. Пару одноцветных столбов, между которыми нет других столбов того же цвета, будем называть хорошей.

Оценка. Пусть $n$ столбов покрашено так, что условие задачи выполнено. Пусть $ni$ — количество столбов $i$ -го цвета (далее считаем, что $ni ≥ 1,$ т.е. все цвета присутствуют, иначе можно увеличить $n,$ добавив столб нового цвета в конец). Пусть $ai$ и $bi$ — номера первого и последнего столбов $i$ -го цвета.

Всего у нас есть

t=(n1− 1)+(n2− 1)+ ...+ (nk − 1)= (n1+n2+ ...+ nk)− k =n − k

хороших пар столбов. Поскольку все расстояния между столбами в хороших парах различны, наименьшее из этих расстояний не меньше 1, следующее — не меньше 2, и т.д. Итак, для суммы $S$ расстояний во всех хороших парах получаем оценку

S ≥ 1+2+ ...+ t= t(t+ 1)∕2

С другой стороны, сумма всех расстояний для $i$ -го цвета равна $b − a. i i$ Поэтому

S = (b1+ ...+ bk)− (a1 +...+ ak)

Сумма $b1+ ...+bk$ не превышает суммы $k$ самых больших среди номеров 1, 2, …, $n,$ а сумма $a1+ ...+ ak$ не меньше, чем сумма $k$ наименьших среди номеров 1, 2, …, $n,$ поэтому

S ≤ (n+ (n− 1)+ ...+(n− k+ 1))− (1+2+ ...+ k)=

= (n− 1)+ ...+ (n− k+1)− (1 +2+ ...+ k)= k(n− k)

Итак,

t(t+1)∕2≤S ≤ kt,

откуда $t≤ 2k− 1$ и

n= k+ t≤3k− 1.

Пример. Годится, например, покраска

1,2,...,k− 1,k,k,k− 1,...,2,1,2,3,...,k

Здесь для цвета 1 единственная хорошая пара, и расстояние между столбами в ней равно $2k− 1.$ Для всех остальных цветов есть две хорошие пары, при этом для цвета 2 имеем расстояния $2k− 3$ и 2, для цвета 3 — расстояния $2k− 5$ и 4, и т.д., для цвета $k$ — расстояния 1 и $2k− 2.$

Ответ:

$3k− 1$

Ошибка.
Попробуйте повторить позже

Задача 9#131385Максимум баллов за задание: 7

Докажите, что для любых трёх положительных вещественных чисел $x,y,z$ выполнено неравенство

∘--2---2 ∘ --2--2- ∘ -2---2- (x − y) 3x + y + (y− z) 3y + z+ (z− x) 3z+ x ≥ 0.

Источники: ВСОШ, РЭ, 2023, 10.10 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1:

Попробуйте оценить каждое слагаемое некоторым выражением так, чтобы сумма выражений равнялась нулю.

Подсказка 2:

Понятно, что хочется оценить корни. Также ясно, что так просто оценить не получится, потому что оценка будет работать по-разному в зависимости от знака разности переменных.

Подсказка 3:

Попробуйте сравнить первое слагаемое в левой части с x² – y² при x ≥ y и при x < y.

Показать доказательство

Докажем, что