Тема 10. Сюжетные текстовые задачи

10.06 Задачи на растворы, смеси и сплавы

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела сюжетные текстовые задачи

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#297

В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?

Показать ответ и решение

Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100 $%$ . До переливания в сосуде А было $3⋅0,17 = 0,51$ литра вещества Х, в сосуде В было $7 ⋅0,19 = 1,33$ литра вещества Х.

После переливания объём вещества Х в сосуде А стал $0,51+ 1,33 = 1,84$ литра, а объём всего раствора $3+ 7 = 10$ литров. Тогда концентрация в процентах составила

1,84 -10-⋅100% = 18,4%.

Ответ: 18,4

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#18129

Имеется два сплава. Первый сплав содержит 45% меди, второй — 20% меди. Масса первого сплава больше массы второго на 30 кг. Из этих двух сплавов получили третий сплав, содержащий 40% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Показать ответ и решение

Пусть $m$ — масса второго сплава в кг. Тогда масса первого сплава равна $m + 30$ кг.

Так как первый сплав содержит 45% меди, то масса меди в кг в нем равна

c1 = 0,45⋅(m +30)= 0,45m +13,5

Аналогично масса меди в кг во втором сплаве равна

c2 = 0,2⋅m = 0,2m

Третий сплав получили из первого и второго, значит, масса третьего сплава в кг равна

m3 = (m + 30)+ m = 2m + 30

Масса меди в кг в третьем сплаве равна

c3 = (0,45m + 13,5)+ 0,2m =0,65m + 13,5

Процентное содержание меди в третьем сплаве равно 40%, то есть

c3 0,65m + 13,5 0,4= m3-= --2m-+-30-- ⇔

⇔ 0,8m+ 12= 0,65m +13,5 ⇔ m = 10

Тогда масса третьего сплава в кг равна

2m + 30= 2⋅10+ 30= 50

Ответ: 50

Ошибка.
Попробуйте повторить позже

Задача 3#23556

Смешали 4 кг 15-процентного водного раствора некоторого вещества с 6 кг 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Показать ответ и решение

Масса в кг чистого вещества в 15-процентном растворе составляет

4⋅0,15= 0,6

Масса в кг чистого вещества в 25-процентном растворе составляет

6⋅0,25= 1,5

Поделив общую массу чистого вещества на суммарную массу смеси и домножив на 100%, получим искомую концентрацию в процентах:

0,6+ 1,5 -4+-6--⋅100%= 21%

Ответ: 21

Ошибка.
Попробуйте повторить позже

Задача 4#23558

Имеются два сплава. Первый содержит 5% никеля, второй — 20% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Показать ответ и решение

Пусть масса первого сплава равна $x$ кг, второго — $y$ кг. Тогда масса никеля в первом сплаве равна $0,05x$ кг, во втором — $0,2y$ кг. Выразив массу и процентное содержание никеля в третьем сплаве через $x$ и $y,$ получим систему:

( ( |{x+ y = 225 |{x +y = 225 |0,05x + 0,2y ⇔ | 0,05(225− y)+ 0,2y (---x+-y--- =0,15 ( ------225-------= 0,15 ( ( |{x+ y = 225 |{y = 33,75−-11,25-= 150 | ⇔ | 0,15 (11,25+ 0,15y = 33,75 (x = 75

Тогда искомая разница в килограммах равна

y− x =150− 75= 75

Ответ: 75

Ошибка.
Попробуйте повторить позже

Задача 5#298

Иван случайно смешал молоко жирностью $2,5%$ и молоко жирностью $6%.$ В итоге у него получилось 5 литров молока жирностью $4,6%.$ Сколько литров молока жирностью $2,5%$ было у Ивана до смешивания?

Показать ответ и решение

Пусть $x$ литров молока жирностью $2,5%$ было у Ивана, тогда

$5− x$ литров молока жирностью $6%$ было у Ивана,

$2,5 100x$ – объём жира в молоке жирностью $2,5%$ , $6 100(5− x)$ – объём жира в молоке жирностью $6%$ .

Так как в итоге жира оказалось $4,6 100 ⋅5 = 0,23$ литра, то:

$2,5x + -6-(5− x) = 0,23 100 100$ , откуда находим $x = 2$ .

Ответ: 2

Ошибка.
Попробуйте повторить позже

Задача 6#299

Один газ в сосуде А содержал $21%$ кислорода, второй газ в сосуде В содержал $5%$ кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит $14,6%$ кислорода. Найдите массу третьего газа. Ответ дайте в граммах.

Показать ответ и решение

Пусть $x$ грамм – масса второго газа, тогда

$x + 300$ грамм – масса первого газа,

$21 100(x + 300)$ грамм – масса кислорода в первом газе,

$5 100x$ грамм – масса кислорода во втором газе,

тогда масса кислорода в третьем газе составляет $14,6(2x+ 300) 100$ грамм.

Так как третий газ возник в результате смешивания первого и второго, то:

-21(x + 300) + -5-x = 14,6-(2x + 300), 100 100 100

откуда находим $x = 600$ . Таким образом, масса третьего газа равна $600 + 600+ 300 = 1500$ грамм.

Ответ: 1500

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#692

Во сколько раз больше должен быть объём $5$ -процентного раствора кислоты, чем объём $10$ -процентного раствора той же кислоты, чтобы при смешивании получить $7$ -процентный раствор?

Показать ответ и решение

Пусть объём $5$ -процентного раствора кислоты равен $x$ литров, а объём $10$ -процентного раствора равен $y$ литров, тогда требуется найти значение величины $x- y$ при условии

x- 3- 0,05x + 0,1y = 0, 07(x + y) ⇔ y = 2 = 1,5,

таким образом, ответ: $1,5$ .

Ответ: 1,5

Ошибка.
Попробуйте повторить позже

Задача 8#694

Половину объёма огурца когда-то занимала вода, потом этот огурец подсох и вода стала занимать лишь $20%$ объёма огурца. Во сколько раз уменьшился объём этого огурца?

Показать ответ и решение

Пусть первоначальный объём огурца составлял $V0$ литров, а конечный объём $V1$ литров. Так как объём сухого вещества не менялся, то

0,5V = 0,8V , 0 1

откуда находим

V0 --- = 1,6, V1

следовательно, объём огурца уменьшился в $1,6$ раз.

Ответ: 1,6

Ошибка.
Попробуйте повторить позже

Задача 9#1626

Мокрая губка содержала 80 $%$ воды, а после выжимания только 20 $%$ . Чему была равна масса мокрой губки, если масса губки после выжимания стала 100 грамм? Ответ дайте в граммах.

Показать ответ и решение

Первый способ:

В выжатой губке $100% − 20% = 80%$ сухого вещества, тогда после выжимания масса сухого вещества губки стала составлять $0,8 ⋅ 100 = 80$ грамм.

Но и до выжимания она была такой же, при этом до выжимания она составляла только $100 − 80 = 20%$ массы мокрой губки, значит масса мокрой губки была $80 : 0,2 = 400$ грамм.

Второй способ:

Пусть $x$ кг – масса мокрой губки, тогда

-x--⋅ 20 г 100

– масса сухого вещества. После выжимания масса сухого вещества стала составлять $100 − 20 = 80%$ от массы выжатой губки (то есть 80 грамм), тогда

-x-- 100 ⋅ 20 = 80,

откуда $x = 400$ грамм.

Ответ: 400

Ошибка.
Попробуйте повторить позже

Задача 10#1627

Сергей смешал раствор, содержащий $20%$ кислоты и раствор, содержащий $40%$ той же кислоты. В итоге у него получился раствор, содержащий $32,5%$ кислоты, причём объём полученного раствора $4$ литра. Сколько литров раствора, содержащего $20%$ кислоты, использовал Сергей при смешивании?

Показать ответ и решение

Пусть $x$ литров раствора, содержащего $20%$ кислоты использовал Сергей при смешивании, тогда

$4 − x$ литров раствора, содержащего $40%$ кислоты использовал Сергей при смешивании,

$20 ---x 100$ – объём кислоты в растворе, содержащем $20%$ кислоты, $40 ----(4 − x) 100$ – объём кислоты в растворе, содержащем $40%$ кислоты.

Так как в итоге кислоты оказалось $32,5 -----⋅ 4 = 1, 3 100$ литра, то:

20-- -40- 100x + 100 (4 − x) = 1,3,

откуда находим $x = 1,5$ .

Ответ: 1,5

Ошибка.
Попробуйте повторить позже

Задача 11#1987

У Риты было два наполовину заполненных $10$ -литровых ведра: одно с краской, а другое с водой. Рита взяла и перелила из ведра с водой в ведро с краской ровно $1$ литр (при помощи ковша объёмом $1$ литр). Затем, немного подумав, она перелила из ведра, которое изначально было с краской, литр в ведро с водой. Вот только она не помнит, перемешивала ли она содержимое ведра, которое изначально было с краской, прежде чем перелить из него литр. Найдите разность между концентрацией воды в ведре с краской и концентрацией краски в ведре с водой.

Показать ответ и решение

Попробуем ответить на вопрос, откуда в ведре с краской вода: это вода, которая была перелита в первый раз, но не ушла при втором переливании. При втором переливании именно её место в ковше заняла краска.

Попробуем ответить на вопрос, откуда в ведре с водой краска: это краска, которая была перелита во второй раз, то есть это та самая краска, которая заняла место навсегда оставшейся в ведре с краской воды, следовательно, объём краски в ведре с водой равен объёму воды в ведре с краской. Так как объёмы содержимого вёдер одинаковы, то и соответствующие концентрации одинаковы. Тогда ответ 0.

Ответ: 0

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#2165

Смешав 25-процентный и 95-процентный растворы кислоты и добавив 20 кг чистой воды, получили 40-процентный раствор кислоты. Если бы вместо 20 кг воды добавили 20 кг 30-процентного раствора той же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 25-процентного раствора использовали для получения смеси?

Показать ответ и решение

Заметим, что вода — это раствор, не содержащий кислоту, то есть содержащий 0% кислоты.

Пусть $x$ кг — масса раствора с 25-процентным содержанием кислоты, $y$ кг — масса раствора с 95-процентным содержанием кислоты. Составим схему, описывающую получение 40-процентного раствора:

$PIC$

Заметим, что суммарное количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.

Если раствор весит $x$ кг, а в нем $25%$ кислоты, то в нем $25 100 ⋅x$ кг кислоты.

Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:

-25 95- -0- 40- 100 ⋅x+ 100 ⋅y+ 100 ⋅20= 100 ⋅(x+ y+ 20)

Аналогично составим схему, описывающую получение 50-процентного раствора:

$PIC$

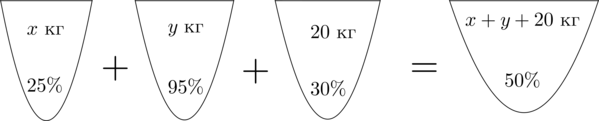
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:

25 95 30 50 100 ⋅x+ 100 ⋅y+ 100 ⋅20= 100 ⋅(x+ y+ 20)

Таким образом, решив систему из полученных двух уравнений, найдем $x.$ Для этого можно умножить оба уравнения на 100, чтобы сделать их проще на вид:

{ 25x +95y +0 = 40(x+ y+ 20) 25x +95y +30⋅20 =50(x+ y+ 20)

Вычтем из второго уравнения первое и получим новую систему:

{25x +95y =40(x+ y+ 20) {5x+ 19y = 8(x+ y+ 20) ⇒ ⇒ 30 ⋅20 = 10(x+ y +20) y =40 − x { { ⇒ 3x − 11(40− x)+ 160 = 0 ⇒ x = 20 y = 40− x y = 20

Таким образом, раствора с 25% кислоты было 20 кг.

Ответ: 20

Ошибка.
Попробуйте повторить позже

Задача 13#2358

Смешав $30$ -процентный и $90$ -процентный растворы кислоты и добавив $10$ кг чистой воды, получили $42$ -процентный раствор кислоты. Если бы вместо $10$ кг воды добавили $10$ кг $50$ -процентного раствора той же кислоты, то получили бы $52$ -процентный раствор кислоты. Сколько килограммов $30$ -процентного раствора использовали для получения смеси?

Показать ответ и решение

Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий $0%$ кислоты.
Пусть $x$ кг – масса раствора с $30$ -процентным содержанием кислоты, $y$ кг – масса раствора с $90$ -процентным содержанием кислоты. Составим схему, описывающую получение $42$ -процентного раствора:

$PIC$

Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит $x$ кг, а в нем $30%$ кислоты, то в килограммах в нем $-30-⋅ x 100$ кислоты.

Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:

30-- -90- -0-- -42- 100 ⋅ x + 100 ⋅ y + 100 ⋅ 10 = 100 ⋅ (x + y + 10 )

Аналогично составим схему, описывающую получение $50$ -процентного раствора:

$PIC$

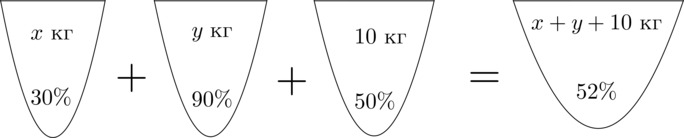
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:

30 90 50 52 ----⋅ x +----⋅ y + ----⋅ 10 =----⋅ (x + y + 10 ) 100 100 100 100

Таким образом, решив систему из полученных двух уравнений, найдем $x$ . Для этого можно умножить оба уравнения на $100$ , чтобы сделать их проще на вид:

{ 30x + 90y + 0 = 42 (x + y + 10 ) 30x + 90y + 50 ⋅ 10 = 52 (x + y + 10 )

Данная система равносильна системе

{ { 4y − x = 35 x = 25 ⇒ 19y − 11x = 10 y = 15

Таким образом, раствора с $30%$ кислоты было $25$ кг.

Ответ: 25

Ошибка.
Попробуйте повторить позже

Задача 14#2668

В лаборатории смешали 10-процентный, 20-процентный и 30-процентный растворы одной и той же кислоты, в результате чего было получено 3 литра 18-процентной кислоты. Какой объём смеси получился бы, если вместо этого смешали 10-процентную кислоту в объёме в два раза большем, чем её было изначально, с 20-процентной кислотой, взятой в том же объёме, что и изначально? Ответ дайте в литрах.

Показать ответ и решение

Пусть изначально было $x$ литров 10-процентного раствора, $y$ литров 20-процентного раствора и $z$ литров 30-процентного раствора. Тогда искомая величина равна $2x +y$ и имеем систему:

( { 0,1x +0,2y+ 0,3z = 0,18(x+ y+ z) ( x+ y+ z = 3 ( { 0,1x +0,2y+ 0,3(3− x− y)= 0,54 ( z = 3− x − y

После подстановки $z$ в первое уравнение системы находим

2x+ y =3,6

Ответ: 3,6

Ошибка.
Попробуйте повторить позже

Задача 15#2733

Азат смешал $10$ -процентный, $20$ -процентный и $30$ -процентный растворы одной и той же кислоты и получил $2$ литра $20$ -процентного раствора. На сколько литров больше было смешано $10$ -процентного раствора, чем $30$ -процентного?

Показать ответ и решение

Пусть у Азата было $x$ литров $10$ -процентного раствора, $y$ литров $20$ -процентного раствора и $z$ литров $30$ -процентного раствора, тогда

0,1x + 0,2y + 0,3z = 0, 2(x + y + z ) ⇔ 0,1z = 0,1x ⇔ x = z,

то есть $10$ -процентного раствора было столько же, сколько и $30$ -процентного, следовательно, ответ: $0$ .

Ответ: 0

Ошибка.
Попробуйте повторить позже

Задача 16#17240

Смешав 15-процентный и 95-процентный растворы кислоты и добавив 10 кг чистой воды, получили 20-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 30-процентный раствор кислоты. Сколько килограммов 15-процентного раствора использовали для получения смеси?

Показать ответ и решение

Пусть $x$ кг — масса 15-процентного раствора, тогда масса чистой кислоты в нем равна $0,15x,$ $y$ кг — масса 95-процентного раствора, $0,95y$ кг — масса чистой кислоты в 95-процентном растворе. В 10 кг 50-процентного раствора 5 кг чистой кислоты. Тогда можем записать уравнение для концентрации в каждом из двух случаев: при добавлении 10 кг чистой воды и 10 кг 50-процентного раствора.

$pict$

Получили, что масса 15-процентного раствора $x =35$ кг.

Ответ: 35

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#20843

Имеется два сосуда. Первый содержит 30 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

Показать ответ и решение

Обозначим процент кислоты в первом растворе через $x,$ $0≤ x≤ 100,$ процент кислоты во втором растворе через $y,$ $0 ≤y ≤ 100.$

Тогда первый раствор содержит $-x-⋅30= 0,3x 100$ кг кислоты, второй раствор содержит $-y-⋅20= 0,2y 100$ кг кислоты. Тогда если смешать эти растворы, то получится раствор весом 50 кг, содержащий $0,3x + 0,2y$ кг кислоты. В то же время известно, что такой раствор содержит 68% кислоты, то есть масса кислоты в этом растворе равна $-68⋅50 =34 100$ кг. Получим уравнение:

0,3x + 0,2y = 34

Рассмотрим теперь результат смешивания равных масс этих двух растворов. Пусть масса каждого из них равна $S$ кг. Тогда после смешивания получится раствор весом $2S$ кг, содержащий $x y 100S+ 100S$ кг кислоты.

Из условия известно, что в полученном растворе будет содержаться 70% кислоты, то есть масса кислоты будет равна $-70 ⋅2S 100$ кг. Получим уравнение:

-x-S + -y-S =-70 ⋅2S ⇔ x+ y = 140 100 100 100

Тогда имеем систему из двух полученных уравнений:

$( ( { 0,3x+ 0,2y = 34 {3x +2y =340 ( ⇔ ( ⇔ x+ y = 140 x +y = 140 ({ ⇔ 3x+ 2y− 2(x+ y)= 340− 2⋅140 ⇔ (x +y = 140 ({ ({ ⇔ x = 60 ⇔ x =60 (x +y = 140 (y =80$

Таким образом, процент кислоты в первом растворе равен 60%, откуда масса кислоты в первом растворе равна $0,3 ⋅60= 18$ кг.

Ответ: 18

Ошибка.
Попробуйте повторить позже

Задача 18#38170

Смешав 41-процентный и 63-процентный растворы кислоты и добавив 10 кг чистой воды, получили 49-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 41-процентного раствора использовали для получения смеси?

Показать ответ и решение

Пусть $x$ кг — масса 41-процентного раствора, $y$ кг — масса 63-процентного раствора. Тогда составим уравнения на кислоту в двух растворах:

{ 0,41x+ 0,63y+ 0⋅10= 0,49(x+ y +10) 0,41x+ 0,63y+ 0,5 ⋅10 = 0,54(x+ y+ 10) { { 41x + 63y = 49(x+ y +10) 500= 5(x+ y+ 10) 41x + 63y +500 =54(x+ y+ 10) ⇔ 14y = 8x+ 490 { { { x= 90− y ⇔ x = 90 − y ⇔ x = 35 14y = 8(90− y)+ 490 22y = 1210 y = 55

Таким образом, масса 41-процентного раствора равна 35 кг.

Ответ: 35

Ошибка.
Попробуйте повторить позже

Задача 19#38240

Имеется два сплава. Первый содержит 50% никеля, второй — 15% никеля. Из этих двух сплавов получили третий сплав с массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Показать ответ и решение

Пусть $x$ кг — масса первого сплава, $175− x$ кг — масса второго. Тогда в первом сплаве $0,5x$ кг никеля, во втором — $0,15(175 − x)$ кг никеля.

Третий сплав содержит 25% никеля, следовательно, получаем уравнение

0,5x+ 0,15(175− x)= 0,25⋅175 0,5x + 0,15⋅175− 0,15x= 175⋅0,25 0,35x= 175⋅0,1 35x= 175⋅10 x= 50

Тогда масса первого сплава равна 50 кг, а масса второго — 125 кг. Значит, масса первого сплава была меньше массы второго на $125− 50= 75$ кг.

Ответ: 75

Ошибка.
Попробуйте повторить позже

Задача 20#58469

Диана смешала раствор, содержащий 30% спирта, и раствор, содержащий 40% спирта. Она знает, что если к смеси добавить 8 литров чистой воды, то получится раствор, содержащий 20% спирта. С другой стороны, если к смеси добавить 5,5 литра раствора, содержащего 5% спирта, то получится раствор, содержащий 25% спирта. Сколько литров 30-процентного раствора спирта смешала Диана?

Показать ответ и решение

Пусть Диана смешала $x$ литров 30-процентного раствора и $y$ литров 40-процентного раствора.

Тогда чистого спирта в смеси:

30- 40- 100 x+ 100y = 0,3x+ 0,4y л

Если к смеси добавить 8 литров воды, то получится 20-процентный раствор:

0,3x + 0,4y =0,2(x+ y+ 8)

В $5,5$ литрах 5-процентного раствора содержится $0,05⋅5,5 = 0,275$ литра спирта. Поэтому если к смеси добавить $5,5$ литра раствора, содержащего 5% спирта, то всего спирта будет