Параллелограмм и ромб (страница 2)
Готовиться с нами - ЛЕГКО!

Найдите большую диагональ ромба, сторона которого равна \(\sqrt3\), а острый угол равен \(60^\circ\).

\(\angle A=60^\circ\).
Проведем диагональ \(BD\). Пусть \(AC\cap BD=O\). Докажем, что \(AC\) – большая диагональ.
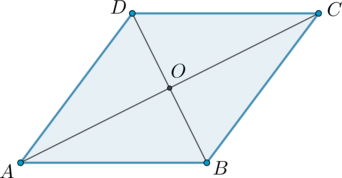
Так как в ромбе, как и в параллелограмме, диагонали точкой пересечения делятся пополам, то \(AO=0,5AC, DO=0,5BD\). Так как в ромбе диагонали являются биссектрисами углов и взаимно перпендикулярны, то \(\angle DAO=30^\circ\), \(\angle AOD=90^\circ\) и соответственно \(\angle ADO=60^\circ\). В треугольнике против большего угла лежит большая сторона, следовательно, \(AO>DO\), значит, \(AC\) – большая диагональ.
Катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, следовательно, \(DO=0,5AD=\frac{\sqrt3}2\). Тогда по теореме Пифагора: \[AO=\sqrt{(\sqrt3)^2-\left(\dfrac{\sqrt3}2\right)^2}=\dfrac32 \quad\Rightarrow\quad AC=3\]
Диагонали ромба относятся как \(4:3\). Периметр ромба равен \(200\). Найдите высоту ромба.
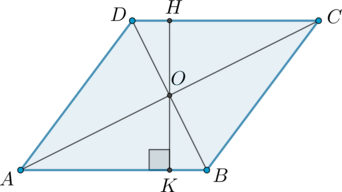
Отрезок \(HK\) – высота ромба. Так как \(AB\parallel DC\) и \(HK\perp AB\), то \(HK\perp DC\).
Так как диагонали ромба делят его на 4 равных прямоугольных треугольника, а у равных треугольников высоты, опущенные к равным сторонам, равны, то \(OK=OH\).
Рассмотрим \(\triangle AOB\). Так как \(AC:BD=4:3\), то также \(AO:BO=4:3\). Пусть \(AO=4x, BO=3x\). Следовательно, \(AB=\sqrt{(4x)^2+(3x)^2}=5x\).
Так как у ромба все стороны равны, то его сторона равна \(200:4=50\), следовательно, \(5x=50\) и \(x=10\).
Высота прямоугольного треугольника \(AOB\), опущенная из вершины прямого угла \(O\), равна \(AO\cdot OB:AB\), следовательно, \[OK=\dfrac{4x\cdot 3x}{5x}=\dfrac{12}5x=24\quad\Rightarrow\quad HK=24\cdot 2=
48\]
В ромбе \(ABCD\) угол \(CDA\) равен \(78^\circ\). Найдите угол \(ACB\). Ответ дайте в градусах.
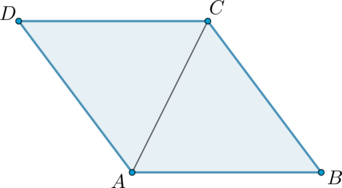
Так как в ромбе диагонали являются биссектрисами углов, то \(\angle ACB=\angle ACD\). Так как у ромба все стороны равны, то \(AD=DC\), следовательно, \(\angle CAD=\angle ACD=x\). Тогда \(x+x+\angle CDA=180^\circ\), откуда \[x=(180^\circ-78^\circ):2=51^\circ\]
В ромбе \(ABCD\) угол \(DAB\) равен \(148^\circ\). Найдите угол \(BDC\). Ответ дайте в градусах.

Так как в ромбе диагонали являются биссектрисами углов, то \(\angle BDC=\angle BDA\). Так как у ромба все стороны равны, то \(AD=AB\), следовательно, \(\angle BDA=\angle DBA=x\). Тогда \(x+x+\angle DAB=180^\circ\), откуда \[x=(180^\circ-148^\circ):2=16^\circ\]
Периметр параллелограмма равен \(100\), его большая сторона равна \(32\). Найдите меньшую сторону параллелограмма.

Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна \(100 : 2 = 50\), значит, меньшая сторона параллелограмма равна \(50 - 32 = 18\).
Периметр параллелограмма равен \(15\). При этом одна сторона этого параллелограмма на \(5\) больше другой. Найдите меньшую сторону параллелограмма.

У параллелограмма противоположные стороны равны. Пусть \(BC = AB + 5\), тогда периметр параллелограмма \(ABCD\) равен \(AB + BC + CD + AD = AB + AB + 5 + AB + AB + 5 = 4\cdot AB + 10 = 15\), откуда находим \(AB = 1,25\). Тогда меньшая сторона параллелограмма равна \(1,25\).
Из точки \(C\) параллелограмма \(ABCD\) опустили перпендикуляр на продолжение стороны \(AD\) за точку \(D\). Этот перпендикуляр пересёк прямую \(AD\) в точке \(E\), причём \(CE = DE\). Найдите \(\angle B\) параллелограмма \(ABCD\). Ответ дайте в градусах.

В равнобедренном треугольнике углы при основании равны, тогда \(\angle EDC = \angle DCE\). Так как \(\angle DEC = 90^{\circ}\), а сумма углов треугольника равна \(180^{\circ}\), то \(\angle EDC = 45^{\circ}\), тогда \(\angle ADC = 180^{\circ} - 45^{\circ} = 135^{\circ}\). Так как в параллелограмме противоположные углы равны, то \(\angle B = \angle ADC = 135^{\circ}\).



