Прямоугольный треугольник
Готовиться с нами - ЛЕГКО!

В \(\triangle ABC\) \(AH\) – высота, \(BD\) – биссектриса, \(O\) – точка пересечения прямых \(AH\) и \(BD\), угол \(ABD\) равен \(62^\circ\). Найдите угол \(AOB\).
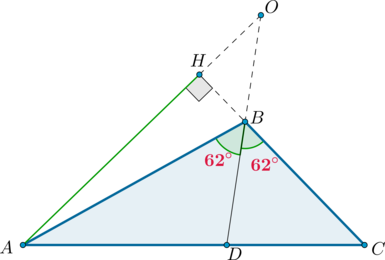
Так как \(BD\) – биссектриса, то \(\angle CBD=\angle ABD= 62^\circ\). \(\angle HBO=\angle CBD=62^\circ\) как вертикальные.
\(\angle OHB=\angle AHB=90^\circ\).
Следовательно, \(\angle AOB=\angle HOB=90^\circ-\angle
HBO=90^\circ-62^\circ=28^\circ\) (так как сумма острых углов в прямоугольном треугольнике равна \(90^\circ\)).
Острый угол \(B\) прямоугольного треугольника \(ABC\) равен \(55^\circ\). Найдите угол между высотой \(CH\) и медианой \(CM\), проведенными из вершины прямого угла \(C\). Ответ дайте в градусах.
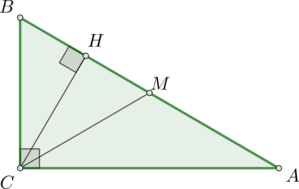
Так как медиана, опущенная из вершины прямого угла треугольника, равна половине гипотенузы, то \(\triangle BMC\) – равнобедренный, то есть \(BM=CM\). Следовательно, \(\angle BCM=\angle B=55^\circ\).
\(\angle BCH=90^\circ-\angle B=35^\circ\). Следовательно, \(\angle
HCM=55^\circ-35^\circ=20^\circ\).
В треугольнике \(ABC\): \(\angle C = 90^{\circ}\), \(CE\) – медиана, \(\angle ACE = 50^{\circ}\). Найдите \(\angle B\). Ответ дайте в градусах.
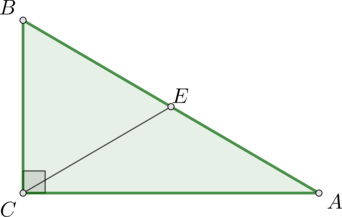
\(\angle ECB = \angle ACB - \angle ACE = 40^{\circ}\). В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда \(CE = BE\), значит треугольник \(CEB\) – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда \(\angle B = \angle ECB = 40^{\circ}\).
В треугольнике \(ABC\): \(\angle B = 90^{\circ}\), \(BE\) – медиана, \(\angle CBE = 25^{\circ}\). Найдите \(\angle AEB\). Ответ дайте в градусах.
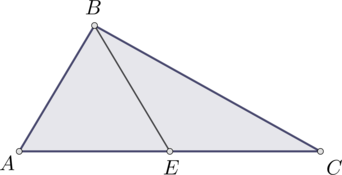
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда \(CE = BE\), значит треугольник \(CEB\) – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда \(\angle C = \angle CBE = 25^{\circ}\).
Так как внешний угол треугольника равен сумме двух углов треугольника не смежных с ним, то \(\angle AEB = \angle C + \angle CBE = 50^{\circ}\).
В треугольнике \(ABC\): \(\angle B = 90^{\circ}\), \(BE\) – медиана, \(\angle CBE = 22^{\circ}\). Найдите \(\angle BAC\). Ответ дайте в градусах.
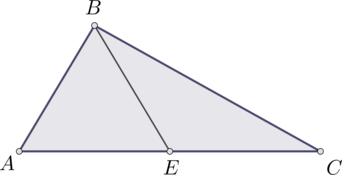
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда \(AE = BE\), значит треугольник \(AEB\) – равнобедренный. В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle ABE\).
Так как \(\angle B = 90^{\circ}\), \(\angle CBE = 22^{\circ}\), то \(\angle ABE = 90^{\circ} - 22^{\circ} = 68^{\circ}\), откуда \(\angle BAC = 68^{\circ}\).
В треугольнике \(ABC\): \(AD\) и \(BE\) – высоты, пересекающиеся в точке \(F\), \(\angle EFD = 104^{\circ}\). Найдите \(\angle C\). Ответ дайте в градусах.
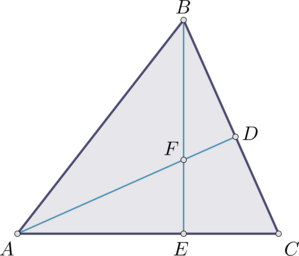
\(\angle AFE = 180^{\circ} - \angle EFD = 76^{\circ}\), тогда \(\angle FAE = 90^{\circ} - \angle AFE = 14^{\circ}\) (так как \(\angle FEA = 90^{\circ}\)). Треугольник \(ADC\) – прямоугольный. \(\angle C = 90^{\circ} - \angle FAE = 76^{\circ}\).
В треугольнике \(ABC\): \(CE\) и \(BF\) – высоты, пересекающиеся в точке \(T\), \(\angle CTB = 152^{\circ}\). Найдите \(\angle A\). Ответ дайте в градусах.
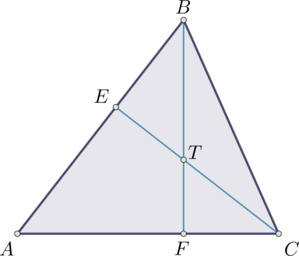
\(\angle FTC = 180^{\circ} - \angle CTB = 28^{\circ}\), тогда \(\angle TCF = 90^{\circ} - \angle FTC = 62^{\circ}\) (так как \(\angle TFC = 90^{\circ}\)). Треугольник \(AEC\) – прямоугольный. \(\angle A = 90^{\circ} - \angle TCF = 28^{\circ}\).



