Прямоугольный треугольник (страница 2)
Готовиться с нами - ЛЕГКО!

В треугольнике \(ABC\): \(\angle A = 60^{\circ}\), \(\angle C = 80^{\circ}\), \(AD\) и \(CE\) – высоты, пересекающиеся в точке \(F\). Найдите \(\angle EFD\). Ответ дайте в градусах.
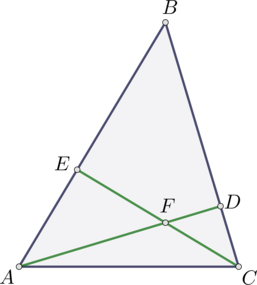
Треугольник \(AEC\) – прямоугольный, \(\angle A = 60^{\circ}\), тогда \(\angle ACE = 90^{\circ} - 60^{\circ} = 30^{\circ}\). Аналогично в треугольнике \(ADC\) находим, что \(\angle DAC = 10^{\circ}\).
Так как сумма углов треугольника равна \(180^{\circ}\), то \(\angle AFC = 180^{\circ} - 10^{\circ} - 30^{\circ} = 140^{\circ}\). Углы \(AFC\) и \(EFD\) равны как вертикальные, тогда \(\angle EFD = 140^{\circ}\).
В треугольнике \(ABC\): \(AE\) и \(BF\) – высоты, пересекающиеся в точке \(O\), \(\angle FBC = 19^{\circ}\). Найдите \(\angle FOE\). Ответ дайте в градусах.
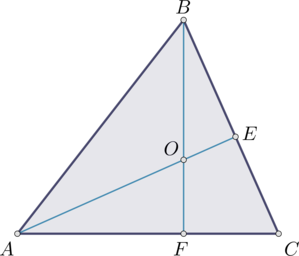
Треугольник \(BOE\) – прямоугольный, \(\angle OBE = 19^{\circ}\), тогда \(\angle BOE = 90^{\circ} - 19^{\circ} = 71^{\circ}\). \(\angle FOE\) – смежный с \(\angle BOE\), тогда их сумма равна \(180^{\circ}\) и, значит, \(\angle FOE = 109^{\circ}\).
В треугольнике \(ABC\): \(BM\) – биссектриса, на сторонах \(AB\) и \(BC\) выбраны точки \(P\) и \(Q\) соответственно, причём перпендикуляр к \(AB\), проходящий через точку \(P\) и перпендикуляр к \(BC\), проходящий через точку \(Q\), пересеклись в точке \(K\), лежащей на биссектрисе \(BM\). Найдите \(PK\), если известно, что \(KQ = 33\).
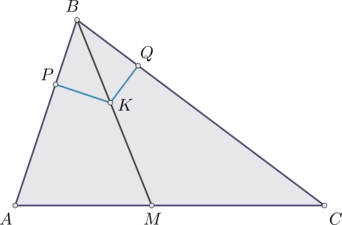
Так как каждая точка биссектрисы угла равноудалена от его сторон, то \(PK = KQ = 33\).
Покажем это подробнее:
треугольники \(PKB\) и \(BKQ\) – прямоугольные, имеющие общую гипотенузу и \(\angle PBK = \angle KBQ\), тогда треугольники \(PKB\) и \(BKQ\) равны по гипотенузе и острому углу, значит, \(PK = KQ\).
В треугольнике \(ABC\) угол \(C\) равен \(90^\circ\), угол \(A\) равен \(30^\circ\), \(AB=2\sqrt3\). Найдите высоту \(CH\).

Так как катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, то \(BC=0,5AB=\sqrt3\).
По свойству прямоугольного треугольника \(\angle BCH=\angle
A=30^\circ\), следовательно, из \(\triangle BCH\): \(HB=0,5
BC=\sqrt3:2\).
Тогда по теореме Пифагора из \(\triangle BCH\): \[CH=\sqrt{BC^2-BH^2}=\sqrt{\dfrac94}=1,5\]
В треугольнике \(ABC\) угол \(C\) равен \(90^\circ\), \(CH\) – высота, угол \(A\) равен \(30^\circ\). Найдите \(AH\), если \(AB=2\).

Так как катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, то \(BC=0,5AB=1\).
Тогда по теореме Пифагора из \(\triangle ABC\): \[AC=\sqrt{AB^2-BC^2}=\sqrt3\] Из прямоугольного \(\triangle AHC\): \(HC=0,5AC=\sqrt3:2\). Тогда по теореме Пифагора \[AH=\sqrt{AC^2-HC^2}=1,5\]
В треугольнике \(ABC\) угол \(C\) равен \(90^\circ\), \(CH\) – высота, угол \(A\) равен \(30^\circ\). Найдите \(BH\), если \(AB=4\).

Так как катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, то \(BC=0,5AB=2\).
По свойству прямоугольного треугольника \(\angle BCH=\angle
A=30^\circ\), следовательно, из \(\triangle BCH\): \(HB=0,5
BC=1\).
В треугольнике \(ABC\) \( \ AB=BC=AC=2\sqrt3\). Найдите высоту \(CH\).
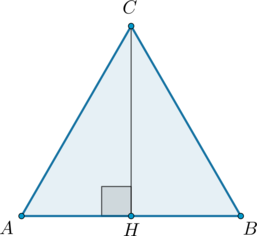
Так как \(AC=BC\), то \(CH\) также является медианой, следовательно, \(AH=0,5 AB=\sqrt3\). Тогда по теореме Пифагора из \(\triangle ACH\): \[CH=\sqrt{AC^2-AH^2}=3\]



