Равнобедренный треугольник (страница 2)
Готовиться с нами - ЛЕГКО!

В треугольнике \(ABC\): \(\angle B = 39^{\circ}\), \(AB = BC\). Найдите внешний угол при вершине \(A\). Ответ дайте в градусах.
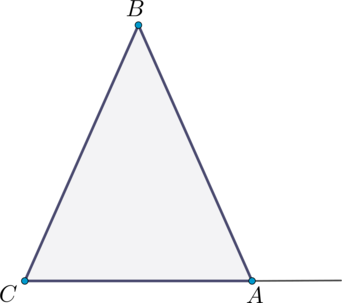
В равнобедренном треугольнике углы при основании равны, тогда \(\angle BAC = \angle C\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(180^{\circ} = 39^{\circ} + \angle A + \angle C = 39^{\circ} + 2\angle C\), откуда \(2\angle C = 141^{\circ}\), тогда \(\angle C = 70,5^{\circ}\).
По теореме о внешнем угле треугольника \(A_{\text{внеш}} = \angle B + \angle C\), тогда искомый угол равен \(39^{\circ} + 70,5^{\circ} = 109,5^{\circ}\).
В треугольнике \(ABC\): \(AB = BC\), внешний угол при вершине \(C\) равен \(108^{\circ}\). Найдите \(\angle B\). Ответ дайте в градусах.
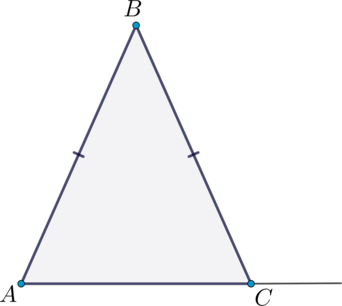
Так как градусная мера развёрнутого угла равна \(180^{\circ}\), то \(\angle ACB = 180^{\circ} - 108^{\circ} = 72^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle ACB = 72^{\circ}\).
Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - \angle A - \angle ACB = 36^{\circ}\).
В треугольнике \(ABC\): \(AB = BC\), внешний угол при вершине \(A\) равен \(112^{\circ}\). Найдите \(\angle B\). Ответ дайте в градусах.

Так как градусная мера развёрнутого угла равна \(180^{\circ}\), то \(\angle BAC = 180^{\circ} - 112^{\circ} = 68^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle C = \angle BAC = 68^{\circ}\).
Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - \angle BAC - \angle C = 44^{\circ}\).
В треугольнике \(ABC\): \(AB = BC\), внешний угол при вершине \(B\) равен \(104^{\circ}\). Найдите \(\angle A\). Ответ дайте в градусах.

Согласно теореме о внешнем угле треугольника, \(\angle A + \angle C = 104^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C\).
Таким образом, \(\angle A = 104^{\circ} : 2 = 52^{\circ}\).
В треугольнике \(ABC\): \(AB = BC\), внешний угол при вершине \(B\) равен \(138^{\circ}\). Найдите \(\angle C\). Ответ дайте в градусах.

Согласно теореме о внешнем угле треугольника, \(\angle A + \angle C = 138^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C\).
Таким образом, \(\angle C = 138^{\circ} : 2 = 69^{\circ}\).
Один из углов равнобедренного треугольника равен \(92^{\circ}\). Найдите какой-нибудь другой его угол.

Сумма углов треугольника равна \(180^{\circ}\). В равнобедренном треугольнике углы при основании равны. Пусть \(92^{\circ}\) – один из углов при основании, тогда сумма углов при основании равна \(92^{\circ} + 92^{\circ} = 184^{\circ} > 180^{\circ}\) – противоречие, значит, \(92^{\circ}\) – угол при вершине.
Сумма углов при основании равна \(180^{\circ} - 92^{\circ} = 88^{\circ}\). Так как углы при основании равны, то оба они по \(88^{\circ} : 2 = 44^{\circ}\).
Один из углов равнобедренного треугольника равен \(124^{\circ}\). Найдите какой-нибудь другой его угол.

Сумма углов треугольника равна \(180^{\circ}\). В равнобедренном треугольнике углы при основании равны. Пусть \(124^{\circ}\) – один из углов при основании, тогда сумма углов при основании равна \(124^{\circ} + 124^{\circ} = 248^{\circ} > 180^{\circ}\) – противоречие, значит, \(124^{\circ}\) – угол при вершине.
Сумма углов при основании равна \(180^{\circ} - 124^{\circ} = 56^{\circ}\). Так как углы при основании равны, то оба они по \(56^{\circ} : 2 = 28^{\circ}\).



