Равнобедренные и равносторонние треугольники (страница 4)
Готовиться с нами - ЛЕГКО!

Основные теоремы:
\(\blacktriangleright\) Вертикальные углы равны, а смежные в сумме дают \(180^\circ\): \(\alpha +\beta =180^\circ\).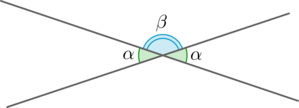
\(\blacktriangleright\) Сумма внутренних углов треугольника равна \(180^\circ\): \(\alpha+\beta+\gamma =180^\circ\)
\(\blacktriangleright\) Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: \(\phi=\alpha+\beta\)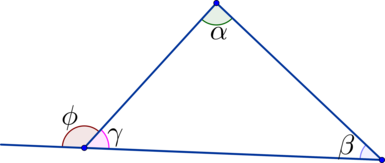
\(\blacktriangleright\) Биссектриса треугольника – отрезок, выходящий из вершины угла и делящий этот угол пополам.
\(\blacktriangleright\) Высота треугольника – отрезок, выходящий из вершины угла под углом \(90^\circ\) к противолежащей стороне (или ее продолжению).
\(\blacktriangleright\) Медиана треугольника – отрезок, выходящий из вершины угла и делящий противолежащую сторону пополам.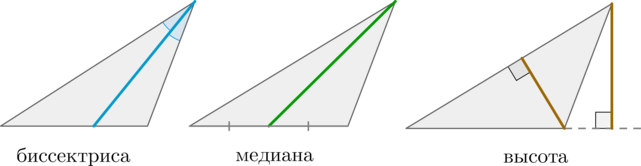
\(\blacktriangleright\) В равнобедренном треугольнике углы при основании равны.
В треугольнике \(ABC\): \(AB = BC\), \(AD\) – высота, \(\angle CAD = 19^{\circ}\). Найдите \(\angle B\). Ответ дайте в градусах.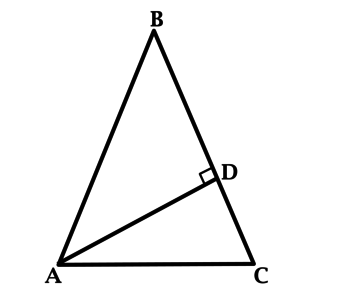
Так как \(AD\) – высота, то \(\angle CDA = 90^{\circ}\), тогда \(\angle CAD + \angle C = 90^{\circ}\). \(\angle CAD = 19^{\circ}\), тогда \(\angle C = 71^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle CAB = \angle C = 71^{\circ}\). Сумма углов треугольника равна \(180^{\circ}\), тогда \(\angle B = 180^{\circ} - \angle C - \angle CAB = 180^{\circ} - 71^{\circ} - 71^{\circ} = 38^{\circ}\).
В треугольнике \(ABC\): \(AC = BC\), \(BD\) – высота, \(\angle ABD = 25^{\circ}\). Найдите \(\angle C\). Ответ дайте в градусах.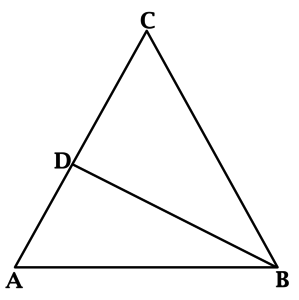
Так как \(BD\) – высота, то \(\angle ADB = 90^{\circ}\), тогда \(\angle A + \angle ABD = 90^{\circ}\). \(\angle ABD = 25^{\circ}\), тогда \(\angle A = 65^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle CBA = \angle A = 65^{\circ}\). Сумма углов треугольника равна \(180^{\circ}\), тогда \(\angle C = 180^{\circ} - \angle A - \angle CBA = 180^{\circ} - 65^{\circ} - 65^{\circ} = 50^{\circ}\).
В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен \(14^\circ\). Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
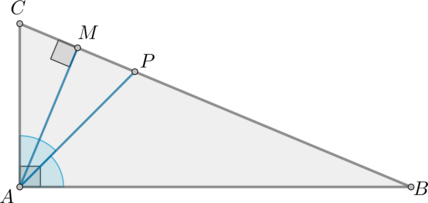
По условию \(\angle MAP=14^\circ\). Так как \(AP\) – биссектриса и \(\angle A=90^\circ\), то \(\angle CAP=45^\circ\), следовательно, \(\angle CAM=45^\circ-14^\circ=31^\circ\).
Тогда \(\angle C=90^\circ-31^\circ=59^\circ\). Следовательно, \(\angle
B=\angle CAM=31^\circ\) – наименьший угол треугольника \(ABC\).
В треугольнике \(ABC\) угол \(C\) равен \(58^\circ\), биссектрисы \(AD\) и \(BE\) пересекаются в точке \(O\). Найдите угол \(AOB\). Ответ дайте в градусах.
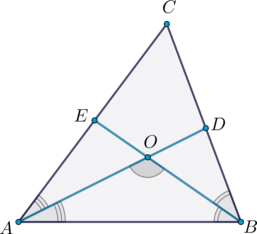
В треугольнике \(ABC\) \(\angle A+\angle B=180^\circ-\angle
C=180^\circ-58^\circ=122^\circ\).
Заметим, что \(\angle AOB=180^\circ-(\angle OAB+\angle
OBA)=180^\circ-0,5(\angle A+\angle B)=180^\circ-0,5\cdot
122^\circ=119^\circ\).
Один из углов равнобедренного треугольника равен \(92^{\circ}\). Найдите какой-нибудь другой его угол.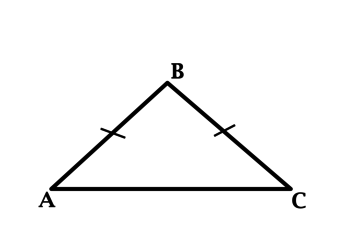
Сумма углов треугольника равна \(180^{\circ}\). В равнобедренном треугольнике углы при основании равны. Пусть \(92^{\circ}\) – один из углов при основании, тогда сумма углов при основании равна \(92^{\circ} + 92^{\circ} = 184^{\circ} > 180^{\circ}\) – противоречие, значит, \(92^{\circ}\) – угол при вершине.
Сумма углов при основании равна \(180^{\circ} - 92^{\circ} = 88^{\circ}\). Так как углы при основании равны, то оба они по \(88^{\circ} : 2 = 44^{\circ}\).
В \(\triangle ABC\) \(AH\) – высота, \(BD\) – биссектриса, \(O\) – точка пересечения прямых \(AH\) и \(BD\), угол \(ABD\) равен \(62^\circ\). Найдите угол \(AOB\).
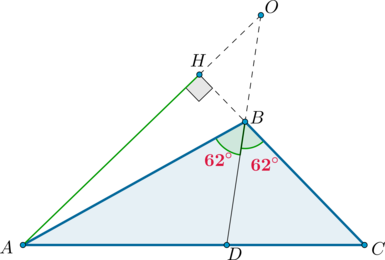
Так как \(BD\) – биссектриса, то \(\angle CBD=\angle ABD= 62^\circ\). \(\angle HBO=\angle CBD=62^\circ\) как вертикальные.
\(\angle OHB=\angle AHB=90^\circ\).
Следовательно, \(\angle AOB=\angle HOB=90^\circ-\angle
HBO=90^\circ-62^\circ=28^\circ\) (так как сумма острых углов в прямоугольном треугольнике равна \(90^\circ\)).
Один из углов равнобедренного треугольника равен \(124^{\circ}\). Найдите какой-нибудь другой его угол.
Сумма углов треугольника равна \(180^{\circ}\). В равнобедренном треугольнике углы при основании равны. Пусть \(124^{\circ}\) – один из углов при основании, тогда сумма углов при основании равна \(124^{\circ} + 124^{\circ} = 248^{\circ} > 180^{\circ}\) – противоречие, значит, \(124^{\circ}\) – угол при вершине.
Сумма углов при основании равна \(180^{\circ} - 124^{\circ} = 56^{\circ}\). Так как углы при основании равны, то оба они по \(56^{\circ} : 2 = 28^{\circ}\).



