Использование различных формул площадей многоугольников (страница 3)
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Треугольник: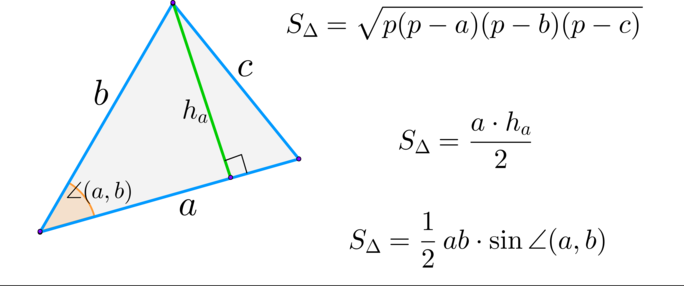
\(\blacktriangleright\) Произвольный выпуклый четырехугольник: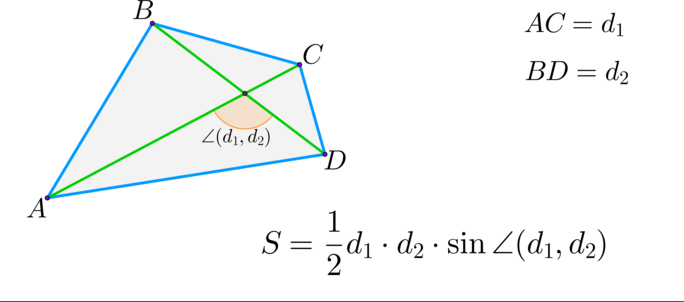
\(\blacktriangleright\) Параллелограмм: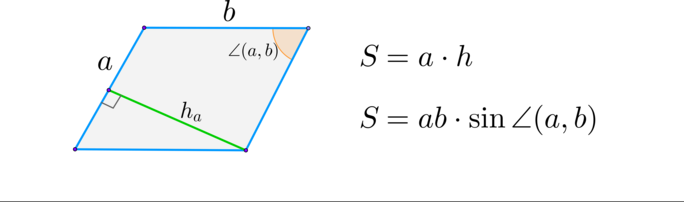
\(\blacktriangleright\) Ромб: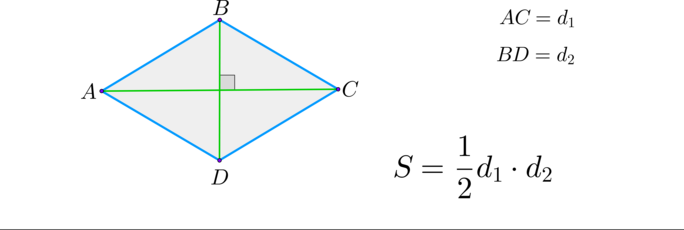
\(\blacktriangleright\) Прямоугольник:
\(\blacktriangleright\) Квадрат: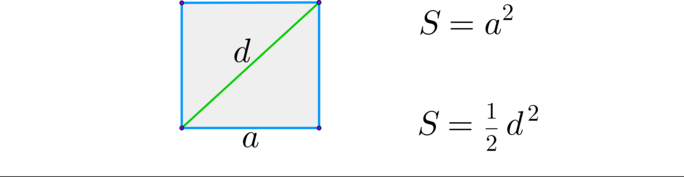
\(\blacktriangleright\) Трапеция:
В выпуклом четырёхугольнике \(ABCD\) диагонали \(AC\) и \(BD\) пересекаются в точке \(O\), \(\angle COD = \mathrm{arcsin}\, 0,85\), \(AC = 5\), \(BD = 4\). Найдите площадь \(ABCD\).
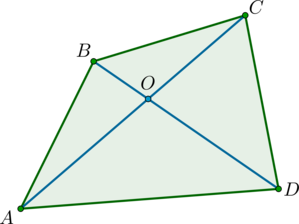
Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними, тогда \(\sin{\angle COD} = \sin{(\mathrm{arcsin}\, 0,85)} = 0,85\), тогда \[S_{ABCD} = 0,5\cdot 0,85\cdot 5 \cdot 4 = 8,5.\]
Найдите площадь треугольника со сторонами \(6\), \(5\) и \(\sqrt{13}\).
Применим формулу Герона для поиска площади треугольника:
\(S=\sqrt{\dfrac{6+5+\sqrt{13}}2\cdot \left(\dfrac{6+5+\sqrt{13}}2-\sqrt{13}\right)\cdot \left(\dfrac{6+5+\sqrt{13}}2-5\right)\cdot \left(\dfrac{6+5+\sqrt{13}}2-6\right)}=\)
\(=\sqrt{\dfrac{6+5+\sqrt{13}}2\cdot \dfrac{6+5-\sqrt{13}}2\cdot \dfrac{6+\sqrt{13}-5}2\cdot \dfrac{5+\sqrt{13}-6}2}=\)
\(=\sqrt{\dfrac{11+\sqrt{13}}2\cdot \dfrac{11-\sqrt{13}}2\cdot \dfrac{\sqrt{13}+1}2\cdot \dfrac{\sqrt{13}-1}2}=\dfrac14\cdot \sqrt{\left(11^2-(\sqrt{13})^2\right)\cdot \left((\sqrt{13})^2-1^2\right)}=\)
\(=\dfrac14\cdot \sqrt{(121-13)(13-1)}=\dfrac14\cdot \sqrt{(4\cdot 3\cdot 9)\cdot (4\cdot 3)}=\dfrac14\cdot 2\cdot 3\cdot 3\cdot 2=9\).
Найдите квадрат площади треугольника со сторонами \(7\), \(11\) и \(6\sqrt6\).
По формуле Герона квадрат площади треугольника равен
\(S^2=\dfrac{7+11+6\sqrt6}2\cdot \left(\dfrac{7+11+6\sqrt6}2-6\sqrt6\right)\cdot \left(\dfrac{7+11+6\sqrt6}2-7\right) \cdot \left( \dfrac{7+11+6\sqrt6}2-11\right)=\)
\(=\dfrac{7+11+6\sqrt6}2\cdot \dfrac{7+11-6\sqrt6}2\cdot \dfrac{11+6\sqrt6-7}2\cdot \dfrac{7+6\sqrt6-11}2=\)
\(=\dfrac1{16}\cdot (18+6\sqrt6)(18-6\sqrt6)(6\sqrt6+4)(6\sqrt6-4)=\)
\(=\dfrac1{16}\cdot 6^2\cdot (3+\sqrt6)(3-\sqrt6)\cdot ((6\sqrt6)^2-4^2)=\dfrac{6^2\cdot 3\cdot 200}{16}=1350\).
Найдите площадь треугольника со сторонами \(22\), \(\sqrt{197}\) и \(\sqrt{65}\).
Рассмотрим этот треугольник. Проведем высоту к стороне, равной \(22\):
Обозначим эту высоту за \(h\), а отрезки, на которые она разбила сторону, за \(x\) и \(22-x\). Запишем теорему Пифагора для двух получившихся прямоугольных треугольников:
\(\begin{cases} 197=h^2+(22-x)^2\\ 65=h^2+x^2 \end{cases} \quad \Leftrightarrow \quad \begin{cases} 197-65=(22-x)^2-x^2\\ 65=h^2+x^2 \end{cases} \quad \Leftrightarrow \)
\(\Leftrightarrow \quad \begin{cases} 132=(22-x-x)(22-x+x)\\ 65=h^2+x^2 \end{cases} \quad \Leftrightarrow \quad \begin{cases} x=8\\ h=1 \end{cases}\)
Таким образом, площадь этого треугольника равна
\[S=\dfrac12\cdot 1\cdot 22=11\]
В треугольнике \(OBH\) точка \(M\) делит сторону \(OB\) на отрезки \(OM = 4, MB = 28, \angle OHM = \angle OBH\). Найдите площадь треугольника \(OHM\), если \(\angle O = 45^\circ\).
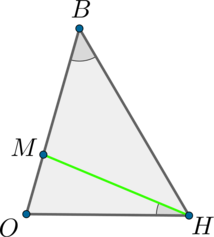
Треугольники \(OMH\) и \(OHB\) подобны по углам, т.к. \(\angle OHM = \angle OBH\), а \(\angle O\) - общий, тогда:
\[\dfrac{OM}{OH} = \dfrac{OH}{OB}\Rightarrow OH^2 = OM\cdot OB\Rightarrow OH = 8\sqrt{2}.\]
\[S_{OHM} = 0,5\cdot 8\cdot \sqrt{2}\cdot 4\cdot \sin{45^\circ} = 16.\]
В параллелограмме \(ABCD\): \(AB = 6\), \(BC = 5\), \(\sin{\angle A} + \sin{\angle B} + \sin{\angle C} + \sin{\angle D} = 3,24\). Найдите площадь параллелограмма \(ABCD\).
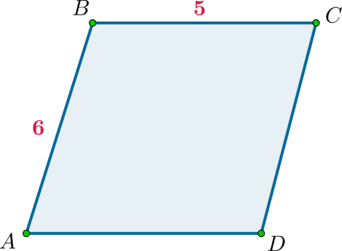
В параллелограмме противоположные углы равны, а односторонние углы в сумме составляют \(180^{\circ}\).
Так как \(\sin{(\pi - \alpha)} = \sin{\alpha}\), то \(\sin{\angle A} + \sin{\angle B} + \sin{\angle C} + \sin{\angle D} = 4 \sin{\angle A}\), откуда находим \(\sin{\angle A} = 0,81\).
Площадь параллелограмма равна произведению двух его непараллельных сторон на синус угла между ними, тогда \[S_{ABCD} = 6\cdot 5\cdot 0,81 = 24,3.\]
В трапеции боковые стороны равны \(12\) и \(12\sqrt5\), угол при меньшей боковой стороне равен \(135^\circ\). Найдите отношение меньшего основания к большему, если площадь трапеции равна \(156\).
Если задача допускает несколько вариантов ответа, внесите в бланк меньший из них.
Рассмотрим трапецию \(ABCD\), где \(AB=12, CD=12\sqrt5\), \(\angle A=45^\circ, \angle B=135^\circ\), и проведем в ней высоты \(BH\) и \(CK\). При этом трапеция может выглядеть двумя разными способами.
1 способ.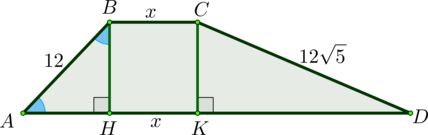
Заметим, что \(\triangle ABH\) – прямоугольный и равнобедренный, тогда \[BH=AH=\dfrac{AB}{\sqrt2}=\dfrac{12}{\sqrt2}=6\sqrt2\]
Значит, из прямоугольного \(\triangle DCK\) можно найти \(KD\):
\[KD^2=CD^2-CK^2=(12\sqrt5)^2-(6\sqrt2)^2=648 \quad \Rightarrow \quad KD=\sqrt{9\cdot 9\cdot 4 \cdot 2}=18\sqrt2\]
Т.к. площадь трапеции равна \(156\), то имеем следующее уравнение:
\[\dfrac{6\sqrt2+18\sqrt2+x+x}2\cdot 6\sqrt2=156 \quad \Rightarrow \quad x=\sqrt2\]
Тогда \(BC:AD=(\sqrt2):(25\sqrt2)=1:25\).
2 способ.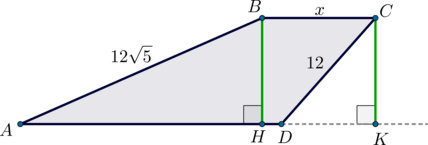
В этом случае, поступая аналогично первому способу, находим \(CK=DK=BH=6\sqrt2\), \(AH=18\sqrt2\), \(AD=18\sqrt2+x-6\sqrt2=12\sqrt2+x\).
Из уравнения \(156=\dfrac{12\sqrt2+x+x}2\cdot 6\sqrt2\) находим \(x=7\sqrt2\).
Значит, \(BC:AD=(7\sqrt2):(19\sqrt2)=7:19\).
Т.к. \(\frac1{25}<\frac7{19}\), то в ответ пойдет \(\frac1{25}=0,04\).



