Окружность, описанная около многоугольника (страница 6)
Готовиться с нами - ЛЕГКО!

Окружность называется описанной около выпуклого многоугольника, если все вершины этого многоугольника лежат на окружности.
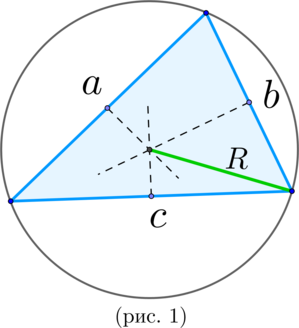
\(\blacktriangleright\) Около любого треугольника можно описать окружность. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника (рис. 1).
Для вписанного треугольника верна формула \[\dfrac{a}{\sin\alpha}=2R,\] где \(\alpha\) – угол треугольника, лежащий против стороны \(a\).
Площадь вписанного треугольника вычисляется по формуле
\[\Large{S_{\triangle}=\dfrac{abc}{4R}}\]
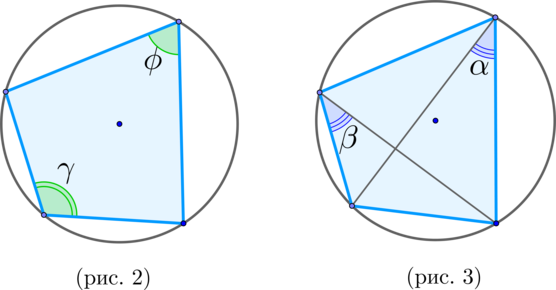
\(\blacktriangleright\) Если около выпуклого четырехугольника описана окружность, то сумма его противоположных углов равна \(\large{\angle\phi + \angle\gamma=180^\circ}\).
И наоборот: Если сумма двух противоположных углов выпуклого четырехугольника равна \(\large{\angle\phi +
\angle\gamma=180^\circ}\), то около него можно описать окружность. (рис. 2)
\(\blacktriangleright\) Около выпуклого четырехугольника описана окружность \(\Leftrightarrow\) \(\large{\angle \alpha =\angle
\beta}\). (рис. 3)
Площадь вписанного четырехугольника вычисляется по формуле
\[{\large{S_{\text{впис.4-к}}=\sqrt{(p-a)(p-b)(p-c)(p-d)},}}\]
где \(a,b,c,d\) – его стороны, \(p=\frac12(a+b+c+d)\) – полупериметр.
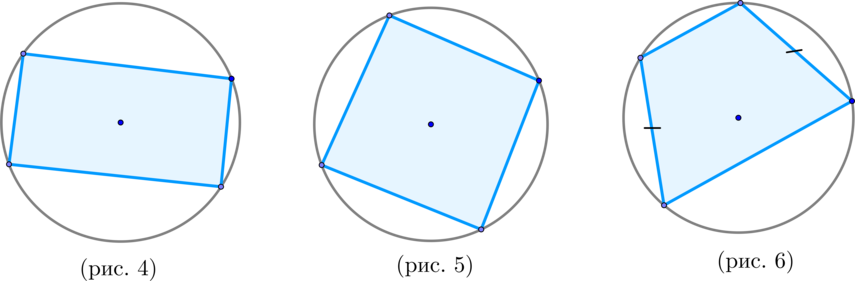
\(\blacktriangleright\) Если около параллелограмма описана окружность, то он – прямоугольник (рис. 4).
\(\blacktriangleright\) Если около ромба описана окружность, то он – квадрат (рис. 5).
\(\blacktriangleright\) Если около трапеции описана окружность, то она равнобедренная.
И наоборот: около равнобедренной (и только равнобедренной) трапеции можно описать окружность (рис. 6).
Окружность проходит через вершины \(B\), \(C\) и \(D\) ромба \(ABCD\), причем точка \(A\) находится вне окружности и \(AD\) является касательной к окружности. \(K\) – точка пересечения отрезка \(AC\) и окружности. Найдите отношение \(CK\) к \(KA\).
Рассмотрим картинку: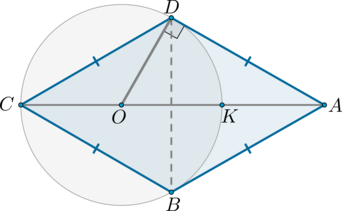
Во-первых, т.к. окружность описана около треугольника \(BCD\), то ее центр \(O\) – точка пересечения серединных перпендикуляров к сторонам треугольника. Следовательно, \(O\) лежит на серединном перпендикуляре к \(BD\) – а это и есть \(CA\) по свойству ромба (диагонали взаимно перпендикулярны). Таким образом, \(CK\) – диаметр этой окружности.
Рассмотрим треугольники \(CDO\) и \(ADK\).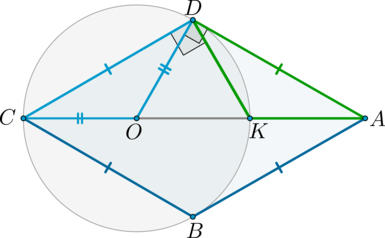
1) Т.к. \(\angle CDK\) опирается на диаметр \(CK\), то он равен \(90^\circ\). Т.к. \(AD\) – касательная к окружности, то угол между ней и радиусом \(OD\) равен \(90^\circ\). Заметим, что углы \(\angle CDK\) и \(\angle ODA\) имеют общую часть – угол \(ODK\). Следовательно, т.к. они равны, то равны и другие их части: \(\angle CDO=\angle ADK=\alpha\).
2) Т.к. треугольник \(CDO\) равнобедренный (\(CO=OD\) – радиусы), то \(\angle DCO=\alpha\). Т.к. треугольник \(CDA\) равнобедренный, то \(\angle DAK=\angle DCO=\alpha\).
3) Таким образом, по стороне и двум прилежащим к ней углам (\(CD=DA, \ \angle DCO=\angle CDO=\angle ADK=\angle DAK\)) треугольники \(CDO\) и \(ADK\) равны. Следовательно, \(KA=CO\).
Значит, \[\dfrac{CK}{KA}=\dfrac{2CO}{CO}=2.\]
Треугольники \(ABC\) и \(ADC\) имеют равные углы \(B\) и \(D\), причем отрезок \(BD\) не пересекает прямую \(AC\). Найдите угол \(DAC\), если угол \(DBC\) равен \(60^\circ\). Ответ дайте в градусах.
Учитывая условие, рисунок будет выглядеть так: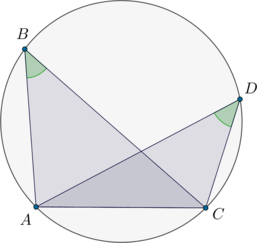
По признаку четырехугольник \(ABDC\) является вписанным, то есть около него можно описать окружность. Следовательно, \(\angle DAC=\angle
DBC=60^\circ\) как вписанные углы, опирающиеся на одну дугу.
Заметим, что фраза “отрезок не пересекает прямую” абсолютно не значит, что отрезок и прямая параллельны! Вот если бы это было сказано о двух прямых – другое дело. Если бы отрезок пересекал прямую, то картинка выглядела бы, например, так: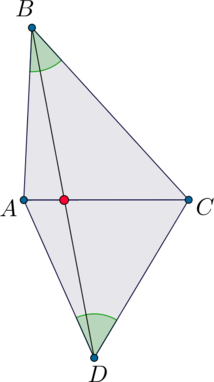
В окружность вписан равносторонний треугольник \(ABC\). Прямые, содержащие медианы этого треугольника, повторно пересекают окружность в точках \(A', B'\) и \(C'\). Найдите площадь фигуры \(\triangle ABC \cap \triangle A'B'C'\), если \(AB=6\sqrt[4]3\).
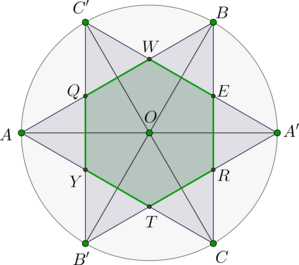
Фигура, равная \(\triangle ABC \cap \triangle A'B'C'\), это шестиугольник \(QWERTY\).
Заметим, что \(\triangle A'B'C'\) тоже правильный, причем равен \(\triangle ABC\). Покажем, что \(\angle A'B'C'\) равен \(60^\circ\).
\(\angle BAA'=30^\circ\), так как \(AA'\) – биссектриса. Аналогично \(\angle BCC'=30^\circ\). Следовательно, \[\buildrel\smile\over{A'BC'}=\buildrel\smile\over{A'B}+
\buildrel\smile\over{BC'}=2\left( \angle BAA'+\angle
BCC'\right)=120^\circ \quad\Rightarrow\quad \angle
A'B'C'=\dfrac12\buildrel\smile\over{A'BC'}=60^\circ.\] Аналогично доказывается, что \(A'=C'=60^\circ\).
Следовательно, \(\triangle A'B'C'\) правильный. А так как радиус описанной около него окружности равен радиусу окружности, описанной около \(\triangle ABC\), то треугольники равны.
Заметим, что \(QWERTY\) – правильный шестиугольник.
У \(\triangle QAY\) луч \(AA'\) содержит и биссектрису, и высоту, следовательно, \(\triangle QAY\) равнобедренный. А так как его угол \(A\) равен \(60^\circ\), то он равносторонний. Аналогично доказывается, что и другие треугольники равносторонние (\(\triangle YB'T, \triangle TCR\) и т.д.).
Так как \(\angle WBA'=\angle ABA'=90^\circ\) (опирается на диаметр), а \(\angle WBE=60^\circ\), то \(\angle EBA'=\angle EA'B=30^\circ\), следовательно, \(EA'=EB\). Следовательно, \(\triangle WBE=\triangle
EA'R\). Аналогично доказывается равенство остальных треугольников.
Следовательно, \(AQ=QW=WB\) и \(AQ+QW+WB=AB=6\sqrt[4]3\), значит, \(QW=2\sqrt[4]3\).
Тогда площадь правильного шестиугольника равна \[S_{QWERTY}=\dfrac{3\sqrt3}2QW^2=18.\]


