Геометрический смысл производной

Прямая $y = kx + b$ касается графика функции $y = f(x)$ в точке $(x_0; f(x_0))$, если она проходит через эту точку и $f'(x_0) = k$.

Угловой коэффициент прямой $y = kx + b$ – это число $k$.

Угол наклона прямой $y = kx + b$ – это угол между этой прямой и положительным направлением оси $Ox$, отсчитываемый в направлении против часовой стрелки. Таким образом, угол наклона прямой лежит в полуинтервале $[0^\circ; 180^\circ)$.

Пример

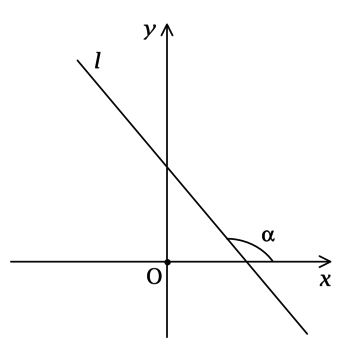
Утверждение

Угловой коэффициент прямой $y=kx+b$ равен тангенсу угла её наклона: $$k=\mathrm{tg}\,\alpha$$

Таким образом, угловой коэффициент касательной $y_k$ к графику функции $y = f(x)$ в точке $(x_0; f(x_0))$ равен тангенсу угла наклона этой касательной.

Утверждение

Угловой коэффициент касательной $y_k=kx+b$ к графику функции $y = f(x)$ в точке $(x_0; f(x_0))$ равен значению производной этой функции $f'(x)$, взятому в точке $x_0$: $$k=f'(x_0)$$