Векторы. Начальные сведения

Определения

Вектор – это направленный отрезок, для которого указано, какая из его граничных точек является началом, а какая – концом.
Если $A$ – начало вектора, $B$ – его конец, то вектор обозначается как $\overrightarrow{AB}$. Вектор также можно обозначать одной маленькой буквой: $\overrightarrow{a}$.

 

Иногда говорят, что вектор – это перемещение из точки $A$ в точку $B$.

 

Длина (или модуль) вектора $\overrightarrow{AB}$ – это длина соответствующего отрезка $AB$.
Обозначение: $|\overrightarrow{AB}|=AB$.

 

Если длина вектора равна нулю (совпадают начало и конец), то такой вектор называют нулевым.

 

Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ($\overrightarrow a, \overrightarrow b$ и $\overrightarrow c$).

В противном случае векторы называются неколлинеарными (например, $\overrightarrow a$ и $\overrightarrow d$).

 

Причем если два коллинеарных вектора направлены в одну сторону, то они называются сонаправленными ($\overrightarrow a$ и $\overrightarrow c$). В противном случае векторы называются противоположно направленными ($\overrightarrow a$ и $\overrightarrow b$).
Обозначение: $\overrightarrow a \uparrow \uparrow \overrightarrow c$, $\overrightarrow a \uparrow \downarrow \overrightarrow b$.

 

Векторы называются равными, если они сонаправлены и их длины равны.

 

Правила сложения коллинеарных векторов:

 

$\blacktriangleright$ Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).

$\blacktriangleright$ Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).

 

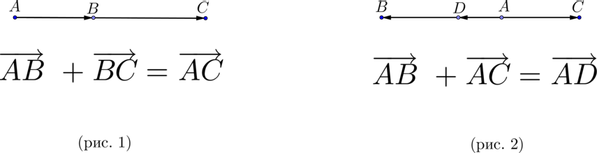
Правила сложения неколлинеарных векторов $\overrightarrow {a}$ и $\overrightarrow{b}$:

 

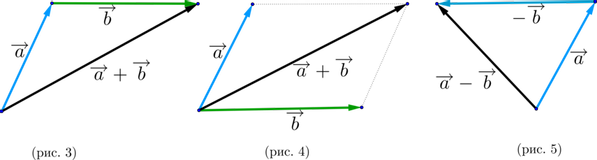
$\blacktriangleright$ Правило треугольника (рис. 3).

Нужно от конца вектора $\overrightarrow {a}$ отложить вектор $\overrightarrow {b}$. Тогда сумма $\overrightarrow {a}+\overrightarrow {b}$ – это вектор, начало которого совпадает с началом вектора $\overrightarrow {a}$, а конец – с концом вектора $\overrightarrow {b}$.

 

$\blacktriangleright$ Правило параллелограмма (рис. 4).

Нужно от начала вектора $\overrightarrow {a}$ отложить вектор $\overrightarrow {b}$. Тогда сумма $\overrightarrow {a}+\overrightarrow {b}$ – вектор, совпадающей с диагональю параллелограмма, построенного на векторах $\overrightarrow {a}$ и $\overrightarrow {b}$ (начало которого совпадает с началом обоих векторов).

 

Определение

Вектор $\overrightarrow {-b}$ – это вектор, противоположно направленный с вектором $\overrightarrow {b}$ и совпадающий с ним по длине.

 

$\blacktriangleright$ Для того, чтобы найти разность двух векторов $\overrightarrow {a}-\overrightarrow{b}$, нужно найти сумму векторов $\overrightarrow {a}$ и $-\overrightarrow{b}$:   $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})$ (рис. 5).

 

Свойства сложения векторов

1. Наличие нейтрального вектора: для любого вектора $\overset{\rightarrow}{a}$ выполнено: $\overset{\rightarrow}{a} + \overset{\rightarrow}{0} = \overset{\rightarrow}{a}$.

2. Наличие обратного вектора: для любого вектора $\overset{\rightarrow}{a}$ выполнено $\overset{\rightarrow}{a} + (-\overset{\rightarrow}{a}) = \overset{\rightarrow}{0}$.

3. Ассоциативность: для любых векторов $\overset{\rightarrow}{a}$, $\overset{\rightarrow}{b}$ и $\overset{\rightarrow}{c}$ выполнено $(\overset{\rightarrow}{a} + \overset{\rightarrow}{b}) + \overset{\rightarrow}{c} = \overset{\rightarrow}{a} + (\overset{\rightarrow}{b} + \overset{\rightarrow}{c})$

4. Коммутативность: для любых векторов $\overset{\rightarrow}{a}$ и $\overset{\rightarrow}{b}$ выполнено $\overset{\rightarrow}{a} + \overset{\rightarrow}{b} = \overset{\rightarrow}{b} + \overset{\rightarrow}{a}$.

 

Замечание

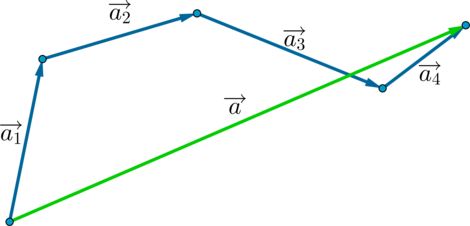
Для того, чтобы сложить несколько вектором, можно отложить их последовательно: каждый следующий от конца предыдущего. Тогда суммой этих векторов будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего: $$\overrightarrow {a_1}+\overrightarrow {a_2}+\overrightarrow {a_3}+ \overrightarrow {a_4}=\overrightarrow {a}$$

 

Определение

Произведением ненулевого вектора $\overrightarrow {a}$ на число $\lambda$ называется такой вектор $\lambda\overrightarrow {a}$, длина которого равна $|\lambda|\cdot |\overrightarrow {a}|$, причем векторы $\overrightarrow {a}$ и $\lambda \overrightarrow {a}$ сонаправлены, если $\lambda>0$, и противоположно направлены, если $\lambda<0$. Если $\lambda=0$, то вектор $\lambda\overrightarrow {a}$ равен нулевому вектору.

 

Свойства произведения вектора на число

1. Сочетательный закон: $k(\lambda\overrightarrow {a})=(k\lambda)\overrightarrow {a}$;

 

2. Распределительный закон 1: $(k+\lambda)\overrightarrow {a}=k\overrightarrow {a}+\lambda\overrightarrow {a}$;

 

2. Распределительный закон 2: $\lambda(\overrightarrow {a}+\overrightarrow {b})=\lambda\overrightarrow {a}+\lambda\overrightarrow {b}$.

 

Теорема

Если $M$ – середина отрезка $PQ$, $O$ – произвольная точка плоскости, то $$\overrightarrow {OM}=\dfrac12 \left(\overrightarrow {OP}+\overrightarrow {OQ}\right)$$