Задачи на теоремы Менелая, Чевы и Стюарта. Формулы для биссектрисы и медианы

$\blacktriangleright$ Теорема Менелая: пусть прямая пересекает треугольник в точке $C_1$ на стороне $AB$, в точке $A_1$ на стороне $BC$ и в точке $B_1$ на продолжении стороны $AC$. Тогда имеет место следующее соотношение:

 

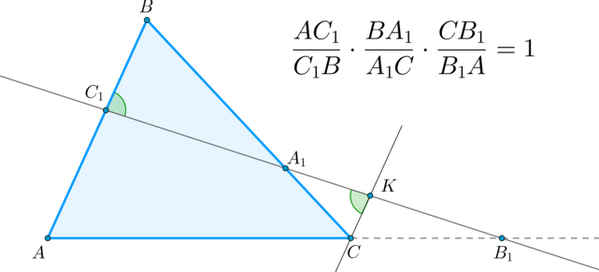
Доказательство: Проведем через точку $C$ прямую параллельно $AB$. Пусть она пересечет $A_1B_1$ в точке $K$. Тогда по двум углам $\triangle A_1BC_1\sim \triangle A_1KC \Rightarrow$

 

$\dfrac{C_1B}{CK}=\dfrac{BA_1}{A_1C}$ или $\dfrac{BA_1\cdot CK}{A_1C\cdot C_1B}=1 \ (*)$

 

Т.к. $\triangle AB_1C_1\sim \triangle CKB_1 \Rightarrow$

 

$\dfrac{CK}{AC_1}=\dfrac{B_1C}{AB_1}$, откуда $CK=\dfrac{B_1C\cdot AC_1}{AB_1}$

 

Подставив последнее равенство в $(*)$ и сгруппировав множители, получим требуемое равенство.

 

$\blacktriangleright$ Теорема, обратная теореме Менелая: пусть в треугольнике точка $B_1$ лежит на продолжении стороны $AC$, а точки $A_1, C_1$ — на сторонах $BC$ и $AB$ соответственно. Тогда, если выполнено равенство $$\dfrac{AB_1}{B_1C}\cdot \dfrac{CA_1}{A_1B}\cdot \dfrac{BC_1}{C_1A}=1,$$ то точки $A_1, B_1, C_1$ лежат на одной прямой.

 

Доказательство: Предположим, что эти три точки не лежат на одной прямой. Тогда прямая $A_1B_1$ пересечет сторону $AB$ в точке $C_2$, отличной от точки $C_1$. Тогда по теореме Менелая для точек $A_1, B_1, C_2$ будет выполнено равенство:

 

$\dfrac{AB_1}{B_1C}\cdot \dfrac{CA_1}{A_1B}\cdot \dfrac{BC_2}{C_2A}=1$

 

Сравнивая это равенство с равенством из условия, получим, что $\dfrac{BC_2}{C_2A}=\dfrac{BC_1}{C_1A}$,

 

то есть точки $C_1$ и $C_2$ поделили отрезок $AB$ в одинаковом соотношении. Значит, эти точки совпадут.

 

Теорема Чевы: пусть на сторонах треугольника $ABC$ выбраны точки $A_1\in BC, B_1\in AC, C_1\in AB$. Отрезки $AA_1, BB_1, CC_1$ пересекаются в одной точке тогда и только тогда, когда выполнено равенство 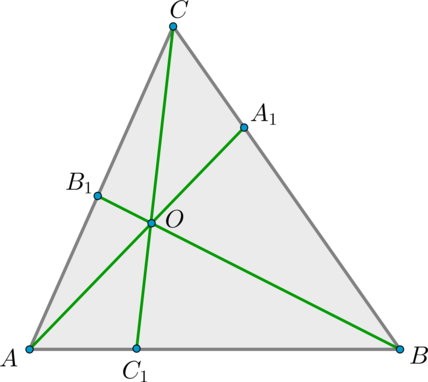$${\large{\dfrac{AB_1}{B_1C}\cdot \dfrac{CA_1}{A_1B}\cdot \dfrac{BC_1}{C_1A}=1}}$$

Доказательство:

1) Докажем, что из пересечения отрезков следует данное равенство:

 

Применим теорему Менелая для $\triangle ABB_1$ и прямой $CC_1$:

 

$\dfrac{AC_1}{C_1B}\cdot \dfrac{BO}{OB_1}\cdot\dfrac{B_1C}{CA}=1$

 

Применим теперь теорему Менелая для $\triangle BB_1C$ и прямой $AA_1$:

 

$\dfrac{BA_1}{A_1C}\cdot \dfrac{CA}{AB_1}\cdot \dfrac{B_1O}{OB}=1$

 

Перемножив полученные два равенства, получим:

 

$\dfrac{AB_1}{B_1C}\cdot\dfrac{CA_1}{A_1B}\cdot\dfrac{BC_1}{C_1A}=1$

 

2) Докажем, что из данного равенства следует, что отрезки пересекутся в одной точке:

 

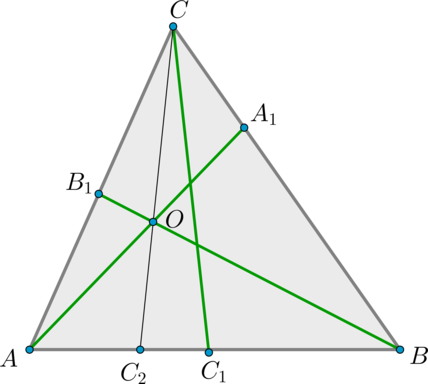
Предположим, что отрезок $CC_1$ не проходит через точку $O$. Тогда проведем отрезок $CC_2$ через точку $O$. Т.к. три отрезка $AA_1, BB_1, CC_2$ пересеклись в одной точке, то для них верно:

 

$\dfrac{AB_1}{B_1C}\cdot\dfrac{CA_1}{A_1B}\cdot\dfrac{BC_2}{C_2A}=1$

 

Сравнивая полученное равенство с равенством из условия, заключаем, что

 

$\dfrac{BC_2}{C_2A}=\dfrac{BC_1}{C_1A}$, т.е. точки $C_1$ и $C_2$ поделили отрезок $AB$ в одинаковом отношении. Это возможно только в том случае, когда эти точки совпадают, т.е. $C_1=C_2$.

 

$\blacktriangleright$ Теорема Стюарта: пусть в треугольнике на стороне $AB$ отмечена точка $P$.
Тогда, если $CP=p, AP=x, BP=y,AC=b, BC=a$, верно следующее соотношение:

 

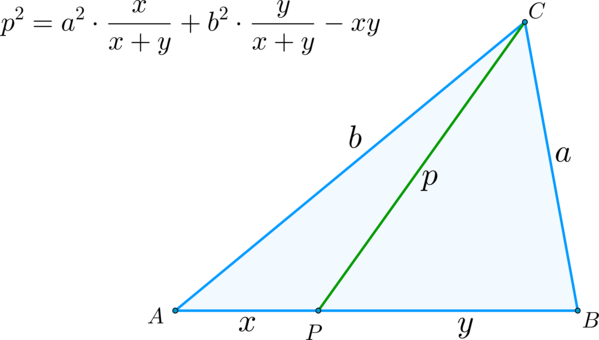
Доказательство: Рассмотрим $\triangle ABC$: по теореме косинусов имеем
$a^2=b^2+(x+y)^2-2b(x+y)\cos \angle A \Rightarrow \cos\angle A=\dfrac{b^2+(x+y)^2-a^2}{2b(x+y)}$

 

Рассмотрим $\triangle ACP$:
$p^2=b^2+x^2-2bx\cos \angle A \Rightarrow \cos\angle A=\dfrac{b^2+x^2-p^2}{2bx}$

 

Следовательно: $\dfrac{b^2+x^2-p^2}{2bx}=\dfrac{b^2+(x+y)^2-a^2}{2b(x+y)} \Rightarrow \dfrac{b^2+x^2-p^2}{x}=\dfrac{b^2+(x+y)^2-a^2}{x+y}$, откуда получаем равенство из условия.

 

$\blacktriangleright$ С помощью теоремы Стюарта выводятся формулы нахождения биссектрис и медиан треугольника:

 

I. Если $l_c$ — биссектриса, проведенная к стороне $c$ и разбивающая эту сторону на отрезки $x$ и $y$, а $a,b$ — две другие его стороны, то $${\large{l^2_c=ab-xy}}$$

Действительно, т.к. $l_c$ — биссектриса, то она делит сторону $c$ на отрезки, пропорциональные прилежащим сторонам, т.е.

 

$\dfrac{x}{y}=\dfrac{b}{a}$

 

Следовательно, можно принять $x=kb, y=ka$, где $k$ — этот коэффициент пропорциональности.

 

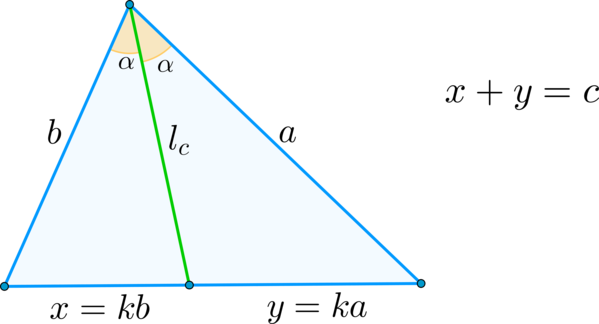
Запишем теорему Стюарта:

 

$l^2_c=a^2\cdot \dfrac x{x+y}+b^2\cdot \dfrac y{x+y}-xy=\dfrac{a^2kb}{k(a+b)}+\dfrac{b^2ka}{k(a+b)}-xy=\dfrac{kab(a+b)}{k(a+b)}-xy=ab-xy$

 

II. Если $m_c$ — медиана, проведенная к стороне $c$ треугольника, а $a,b$ — две другие его стороны, то $${\large{m^2_c=\dfrac{2a^2+2b^2-c^2}4}}$$

Действительно, т.к. $m_c$ — медиана, то $x=y$. Подставив это в равенство Стюарта, получим формулу вычисления медианы треугольника.