Пирамида
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#159
Определение
Пирамида – это многогранник, составленный из многоугольника и треугольников с общей вершиной (не лежащей в плоскости многоугольника) и противолежащими ей сторонами, совпадающими со сторонами многоугольника.
Обозначение: .
Пример: пятиугольная пирамида .
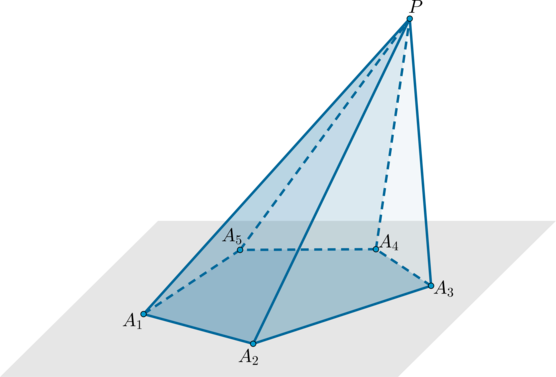
Треугольники и т.д. называются боковыми гранями пирамиды, отрезки и т.д. – боковыми ребрами, многоугольник – основанием, точка – вершиной.
Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида, в основании которой лежит треугольник, называется тетраэдром.
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:
боковые ребра пирамиды равны;
высота пирамиды проходит через центр описанной около основания окружности;
боковые ребра наклонены к плоскости основания под одинаковым углом.
боковые грани наклонены к плоскости основания под одинаковым углом.
Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.
Теорема
Условия эквивалентны.
Доказательство
Проведем высоту пирамиды . Пусть – плоскость основания пирамиды.
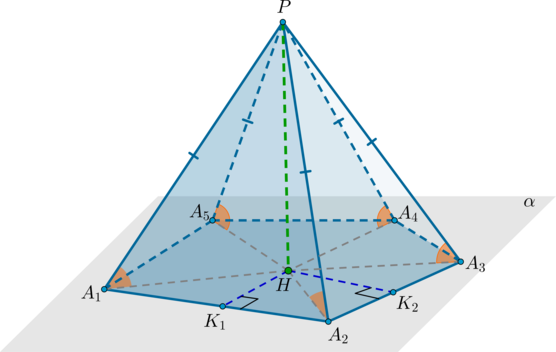
1) Докажем, что из следует . Пусть .
Т.к. , то перпендикулярна любой прямой, лежащей в этой плоскости, значит, треугольники – прямоугольные. Значит, эти треугольники равны по общему катету и гипотенузам . Значит, . Значит, точки находятся на одинаковом расстоянии от точки , следовательно, лежат на одной окружности с радиусом . Эта окружность по определению и есть описанная около многоугольника .
2) Докажем, что из следует .
Аналогично первому пункту треугольники прямоугольные и равны по двум катетам. Значит, равны и их углы, следовательно, .
3) Докажем, что из следует .
Аналогично первому пункту треугольники прямоугольные и по катету и острому углу. Значит, равны и их гипотенузы, то есть .
4) Докажем, что из следует .
Т.к. в правильном многоугольнике совпадают центры описанной и вписанной окружности (вообще говоря, эта точка называется центром правильного многоугольника), то – центр вписанной окружности. Проведем перпендикуляры из точки на стороны основания: и т.д. Это – радиусы вписанной окружности (по определению). Тогда по ТТП ( – перпендикуляр на плоскость, и т.д. – проекции, перпендикулярные сторонам) наклонные и т.д. перпендикулярны сторонам и т.д. соответственно. Значит, по определению равны углам между боковыми гранями и основанием. Т.к. треугольники равны (как прямоугольные по двум катетам), то и углы равны.
5) Докажем, что из следует .
Аналогично четвертому пункту треугольники равны (как прямоугольные по катету и острому углу), значит, равны отрезки . Значит, по определению, – центр вписанной в основание окружности. Но т.к. у правильных многоугольников центры вписанной и описанной окружности совпадают, то – центр описанной окружности. Чтд.
Следствие
Боковые грани правильной пирамиды – равные равнобедренные треугольники.
Определение
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.
Важные замечания
1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).
2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).
3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).
4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.
Определение
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.
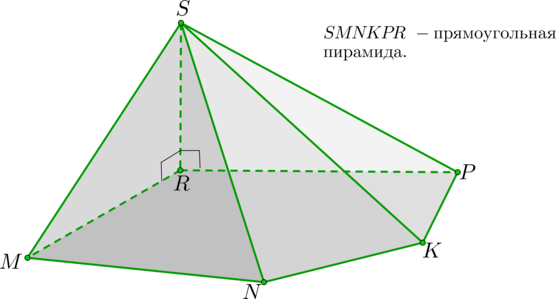
Важные замечания
1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть – высота.
2. Т.к. перпендикулярно любой прямой из основания, то – прямоугольные треугольники.
3. Треугольники – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.
Теорема
Объем пирамиды равен трети произведения площади основания на высоту пирамиды:
Следствия
Пусть – сторона основания, – высота пирамиды.
1. Объем правильной треугольной пирамиды равен ,
2. Объем правильной четырехугольной пирамиды равен .
3. Объем правильной шестиугольной пирамиды равен .
4. Объем правильного тетраэдра равен .
Теорема
Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.
Определение
Рассмотрим произвольную пирамиду . Проведем через некоторую точку, лежащую на боковом ребре пирамиды, плоскость параллельно основанию пирамиды. Данная плоскость разобьет пирамиду на два многогранника, один из которых – пирамида (), а другой называется усеченная пирамида ().
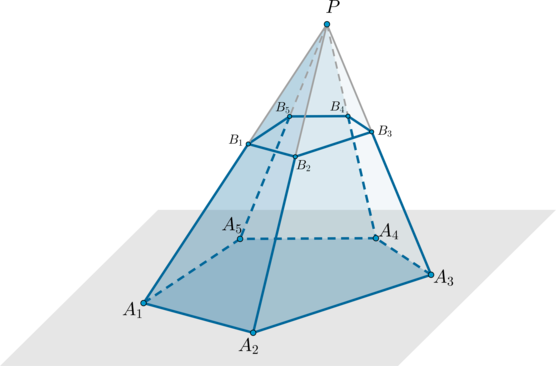
Усеченная пирамида имеет два основания – многоугольники и , которые подобны друг другу.
Высота усеченной пирамиды – это перпендикуляр, проведенный из какой-нибудь точки верхнего основания к плоскости нижнего основания.
Важные замечания
1. Все боковые грани усеченной пирамиды – трапеции.
2. Отрезок, соединяющий центры оснований правильной усеченной пирамиды (то есть пирамиды, полученной сечением правильной пирамиды), является высотой.
