Построение сечений

Определение

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

 

Замечание

Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.

 

Важные определения

1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

 

2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.

 

3. Прямая и плоскость параллельны, если они не имеют общих точек.

 

4. Две плоскости параллельны, если они не имеют общих точек.

 

5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен $90^\circ$.

 

6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

 

7. Две плоскости называются перпендикулярными, если угол между ними равен $90^\circ$.

 

Важные аксиомы

1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

 

2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

 

3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

 

Важные теоремы

1. Если прямая $a$, не лежащая в плоскости $\pi$, параллельна некоторой прямой $p$, лежащей в плоскости $\pi$, то она параллельна данной плоскости.

 

2. Пусть прямая $p$ параллельна плоскости $\mu$. Если плоскость $\pi$ проходит через прямую $p$ и пересекает плоскость $\mu$, то линия пересечения плоскостей $\pi$ и $\mu$ — прямая $m$ — параллельна прямой $p$.

 

3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

 

4. Если две параллельные плоскости $\alpha$ и $\beta$ пересечены третьей плоскостью $\gamma$, то линии пересечения плоскостей также параллельны:

$$\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b$$

 

5. Пусть прямая $l$ лежит в плоскости $\lambda$. Если прямая $s$ пересекает плоскость $\lambda$ в точке $S$, не лежащей на прямой $l$, то прямые $l$ и $s$ скрещиваются.

 

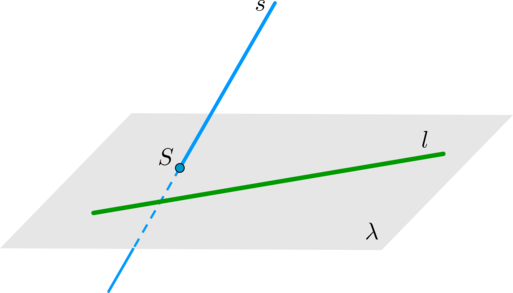
6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

 

7. Теорема о трех перпендикулярах.

Пусть $AH$ – перпендикуляр к плоскости $\beta$. Пусть $AB, BH$ – наклонная и ее проекция на плоскость $\beta$. Тогда прямая $x$ в плоскости $\beta$ будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.

 

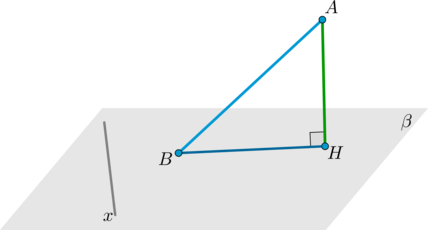
8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.

 

Замечание

Еще один важный факт, часто использующийся для построения сечений:

для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.

 

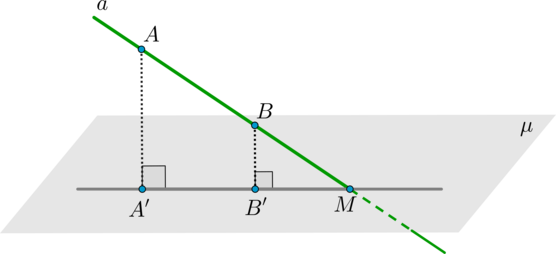
Для этого из двух произвольных точек $A$ и $B$ прямой $a$ проведем перпендикуляры на плоскость $\mu$ – $AA'$ и $BB'$ (точки $A', B'$ называются проекциями точек $A,B$ на плоскость). Тогда прямая $A'B'$ – проекция прямой $a$ на плоскость $\mu$. Точка $M=a\cap A'B'$ и есть точка пересечения прямой $a$ и плоскости $\mu$.

 

Причем заметим, что все точки $A, B, A', B', M$ лежат в одной плоскости.

 

Пример 1.

Дан куб $ABCDA'B'C'D'$. $A'P=\dfrac 14AA', \ KC=\dfrac15 CC'$. Найдите точку пересечения прямой $PK$ и плоскости $ABC$.

 

Решение

1) Т.к. ребра куба $AA', CC'$ перпендикулярны $(ABC)$, то точки $A$ и $C$ — проекции точек $P$ и $K$. Тогда прямая $AC$ – проекция прямой $PK$ на плоскость $ABC$. Продлим отрезки $PK$ и $AC$ за точки $K$ и $C$ соответственно и получим точку пересечения прямых – точку $E$.

 

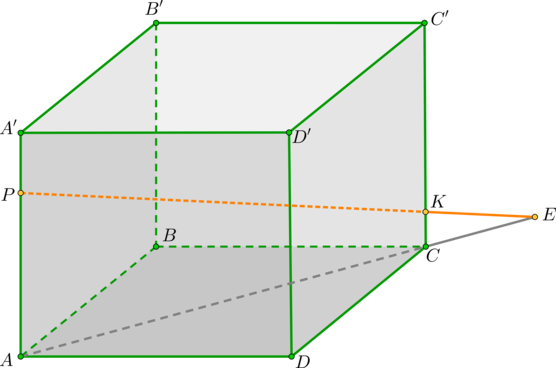
2) Найдем отношение $AC:EC$. $\triangle PAE\sim \triangle KCE$ по двум углам ($\angle A=\angle C=90^\circ, \angle E$ – общий), значит, $$\dfrac{PA}{KC}=\dfrac{EA}{EC}$$

Если обозначить ребро куба за $a$, то $PA=\dfrac34a, \ KC=\dfrac15a, \ AC=a\sqrt2$. Тогда:

$$\dfrac{\frac34a}{\frac15a}=\dfrac{a\sqrt2+EC}{EC} \Rightarrow EC=\dfrac{4\sqrt2}{11}a \Rightarrow AC:EC=4:11$$

Пример 2.

Дана правильная треугольная пирамида $DABC$ с основанием $ABC$, высота которой равна стороне основания. Пусть точка $M$ делит боковое ребро пирамиды в отношении $1:4$, считая от вершины пирамиды, а $N$ – высоту пирамиды в отношении $1:2$, считая от вершины пирамиды. Найдите точку пересечения прямой $MN$ с плоскостью $ABC$.

 

Решение

1) Пусть $DM:MA=1:4, \ DN:NO=1:2$ (см. рисунок). Т.к. пирамида правильная, то высота падает в точку $O$ пересечения медиан основания. Найдем проекцию прямой $MN$ на плоскость $ABC$. Т.к. $DO\perp (ABC)$, то и $NO\perp (ABC)$. Значит, $O$ – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр $MQ$ из точки $M$ на плоскость $ABC$. Точка $Q$ будет лежать на медиане $AK$.
Действительно, т.к. $MQ$ и $NO$ перпендикулярны $(ABC)$, то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки $M, N, O$ лежат в одной плоскости $ADK$, то и точка $Q$ будет лежать в этой плоскости. Но еще (по построению) точка $Q$ должна лежать в плоскости $ABC$, следовательно, она лежит на линии пересечения этих плоскостей, а это – $AK$.

 

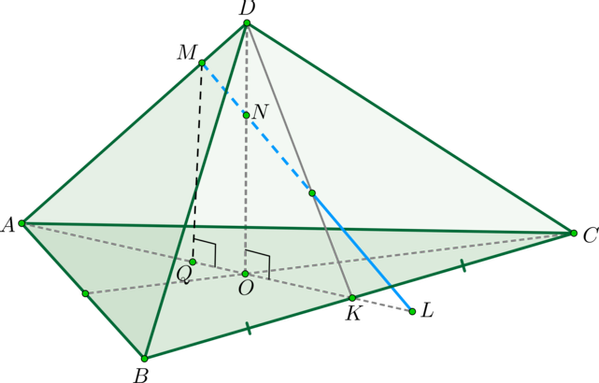
Значит, прямая $AK$ и есть проекция прямой $MN$ на плоскость $ABC$. $L$ – точка пересечения этих прямых.

 

2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки $L$ (например, на нашем чертеже точка $L$ лежит вне отрезка $OK$, хотя она могла бы лежать и внутри него; а как правильно?).

 

Т.к. по условию сторона основания равна высоте пирамиды, то обозначим $AB=DO=a$. Тогда медиана $AK=\dfrac{\sqrt3}2a$. Значит, $OK=\dfrac13AK=\dfrac 1{2\sqrt3}a$. Найдем длину отрезка $OL$ (тогда мы сможем понять, внутри или вне отрезка $OK$ находится точка $L$: если $OL>OK$ – то вне, иначе – внутри).

 

а) $\triangle AMQ\sim \triangle ADO$ по двум углам ($\angle Q=\angle O=90^\circ, \ \angle A$ – общий). Значит,

$$\dfrac{MQ}{DO}=\dfrac{AQ}{AO}=\dfrac{MA}{DA}=\dfrac 45 \Rightarrow MQ=\dfrac 45a, \ AQ=\dfrac 45\cdot \dfrac 1{\sqrt3}a$$

Значит, $QK=\dfrac{\sqrt3}2a-\dfrac 45\cdot \dfrac 1{\sqrt3}a=\dfrac7{10\sqrt3}a$.

 

б) Обозначим $KL=x$.
$\triangle LMQ\sim \triangle LNO$ по двум углам ($\angle Q=\angle O=90^\circ, \ \angle L$ – общий). Значит,

$$\dfrac{MQ}{NO}=\dfrac{QL}{OL} \Rightarrow \dfrac{\frac45 a}{\frac 23a} =\dfrac{\frac{7}{10\sqrt3}a+x}{\frac1{2\sqrt3}a+x} \Rightarrow x=\dfrac a{2\sqrt3} \Rightarrow OL=\dfrac a{\sqrt3}$$

Следовательно, $OL>OK$, значит, точка $L$ действительно лежит вне отрезка $AK$.

 

Замечание

Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что $x$ – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки $L$ (то есть, что она находится внутри отрезка $AK$).

 

Пример 3

Дана правильная четырехугольная пирамида $SABCD$. Найдите сечение пирамиды плоскостью $\alpha$, проходящей через точку $C$ и середину ребра $SA$ и параллельной прямой $BD$.

 

Решение

1) Обозначим середину ребра $SA$ за $M$. Т.к. пирамида правильная, то высота $SH$ пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость $SAC$. Отрезки $CM$ и $SH$ лежат в этой плоскости, пусть они пересекаются в точке $O$.

 

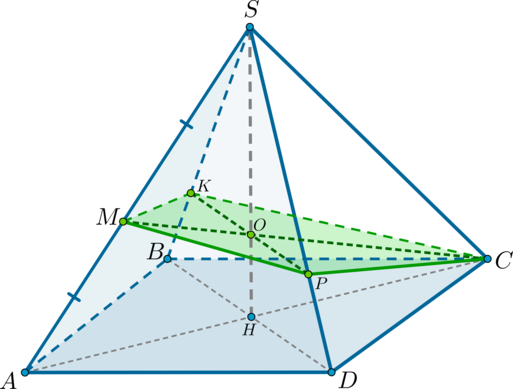
Для того, чтобы плоскость $\alpha$ была параллельна прямой $BD$, она должна содержать некоторую прямую, параллельную $BD$. Точка $O$ находится вместе с прямой $BD$ в одной плоскости – в плоскости $BSD$. Проведем в этой плоскости через точку $O$ прямую $KP\parallel BD$ ($K\in SB, P\in SD$). Тогда, соединив точки $C, P, M, K$, получим сечение пирамиды плоскостью $\alpha$.

 

2) Найдем отношение, в котором делят точки $K$ и $P$ ребра $SB$ и $SD$. Таким образом мы полностью определим построенное сечение.

 

Заметим, что так как $KP\parallel BD$, то по теореме Фалеса $\dfrac{SB}{SK}=\dfrac{SD}{SP}$. Но $SB=SD$, значит и $SK=SP$. Таким образом, можно найти только $SP:PD$.

 

Рассмотрим $\triangle ASC$. $CM, SH$ – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении $2:1$, считая от вершины, то есть $SO:OH=2:1$.

 

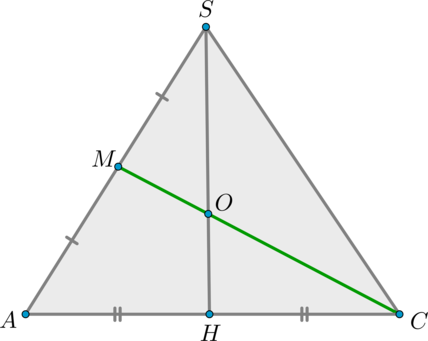
Теперь по теореме Фалеса из $\triangle BSD$: $\dfrac{SP}{PD}=\dfrac{SO}{OH}=\dfrac21$.

 

3) Заметим, что по теореме о трех перпендикулярах $CO\perp BD$ как наклонная ($OH$ – перпендикуляр на плоскость $ABC$, $CH\perp BD$ – проекция). Значит, $CO\perp KP$. Таким образом, сечением является четырехугольник $CPMK$, диагонали которого взаимно перпендикулярны.

 

Пример 4

Дана прямоугольная пирамида $DABC$ с ребром $DB$, перпендикулярным плоскости $ABC$. В основании лежит прямоугольный треугольник с $\angle B=90^\circ$, причем $AB=DB=CB$. Проведите через прямую $AB$ плоскость, перпендикулярную грани $DAC$, и найдите сечение пирамиды этой плоскостью.

 

Решение

1) Плоскость $\alpha$ будет перпендикулярна грани $DAC$, если она будет содержать прямую, перпендикулярную $DAC$. Проведем из точки $B$ перпендикуляр на плоскость $DAC$ — $BH$, $H\in DAC$.

 

Проведем вспомогательные $BK$ – медиану в $\triangle ABC$ и $DK$ – медиану в $\triangle DAC$.
Т.к. $AB=BC$, то $\triangle ABC$ – равнобедренный, значит, $BK$ – высота, то есть $BK\perp AC$.
Т.к. $AB=DB=CB$ и $\angle ABD=\angle CBD=90^\circ$, то $\triangle ABD=\triangle CBD$, следовательно, $AD=CD$, следовательно, $\triangle DAC$ – тоже равнобедренный и $DK\perp AC$.

 

Применим теорему о трех перпендикулярах: $BH$ – перпендикуляр на $DAC$; наклонная $BK\perp AC$, значит и проекция $HK\perp AC$. Но мы уже определили, что $DK\perp AC$. Таким образом, точка $H$ лежит на отрезке $DK$.

 

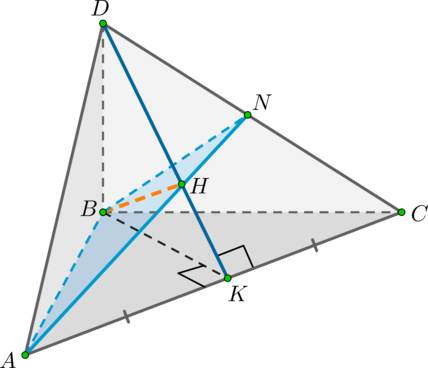
Соединив точки $A$ и $H$, получим отрезок $AN$, по которому плоскость $\alpha$ пересекается с гранью $DAC$. Тогда $\triangle ABN$ – искомое сечение пирамиды плоскостью $\alpha$.

 

2) Определим точное положение точки $N$ на ребре $DC$.

 

Обозначим $AB=CB=DB=x$. Тогда $BK$, как медиана, опущенная из вершины прямого угла в $\triangle ABC$, равна $\frac12 AC$, следовательно, $BK=\frac12 \cdot \sqrt2 x$.

 

Рассмотрим $\triangle BKD$. Найдем отношение $DH:HK$.

 

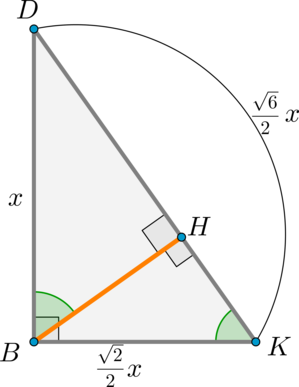
Заметим, что т.к. $BH\perp (DAC)$, то $BH$ перпендикулярно любой прямой из этой плоскости, значит, $BH$ – высота в $\triangle DBK$. Тогда $\triangle DBH\sim \triangle DBK$, следовательно

$$\dfrac{DH}{DB}=\dfrac{DB}{DK} \Rightarrow DH=\dfrac{\sqrt6}3x \Rightarrow HK=\dfrac{\sqrt6}6x \Rightarrow DH:HK=2:1$$

 

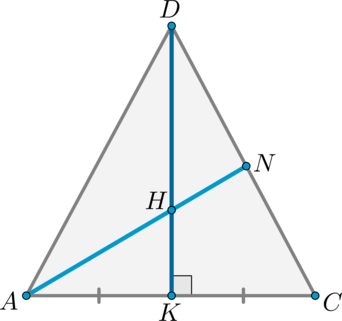
Рассмотрим теперь $\triangle ADC$. Медианы треугольника точной пересечения делятся в отношении $2:1$, считая от вершины. Значит, $H$ – точка пересечения медиан в $\triangle ADC$ (т.к. $DK$ – медиана). То есть $AN$ – тоже медиана, значит, $DN=NC$.