Введение в планиметрию. Основные факты о треугольниках

$${\Large{\text{Основные сведения}}}$$

Определения

Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от $0^\circ$ до $180^\circ$ включительно.

Угол $\alpha$ называется острым, если $0^\circ<\alpha<90^\circ$, прямым – если $\alpha=90^\circ$, тупым – если $90^\circ<\alpha<180^\circ$, и развернутым – если $\alpha=180^\circ$.

 

Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

 

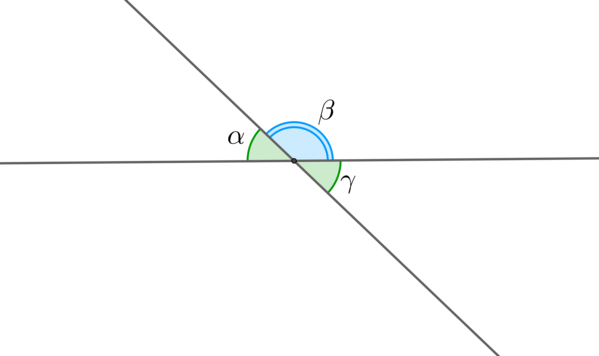
Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.

Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.

 

Теорема

Смежные углы $\alpha$ и $\beta$ в сумме дают $180^\circ$.

Вертикальные углы равны: $\alpha=\gamma$.

 

Определения

Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.

Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.

 

Теоремы: признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

 

2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

 

3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.  

Определение

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

 

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

 

Две прямые называются перпендикулярными, если угол между ними равен $90^\circ$.

 

Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом $90^\circ$.

 

Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

 

Замечание

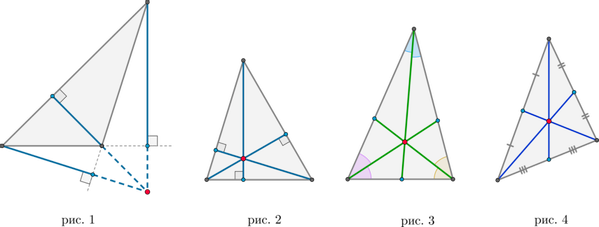
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).

 

Теорема

В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

 

$${\Large{\text{Параллельные прямые}}}$$

Определение

Две различные прямые на плоскости называются параллельными, если они не пересекаются.

 

Замечание

Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.

 

Аксиома параллельных прямых

Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.

 

Следствия из аксиомы

1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.

 

2. Две прямые, параллельные третьей прямой, параллельны.

 

Теоремы: признаки параллельности прямых

1. Если при пересечении двух прямых $a$ и $b$ секущей $c$ накрест лежащие углы равны: $\angle 1=\angle 2$, то такие прямые параллельны.

 

2. Если при пересечении двух прямых $a$ и $b$ секущей $c$ сумма односторонних углов $\angle 1$ и $\angle 3$ равна $180^\circ$, то такие прямые параллельны.

 

3. Если при пересечении двух прямых $a$ и $b$ секущей $c$ соответственные углы равны: $\angle 1=\angle 4$, то такие прямые параллельны.

 

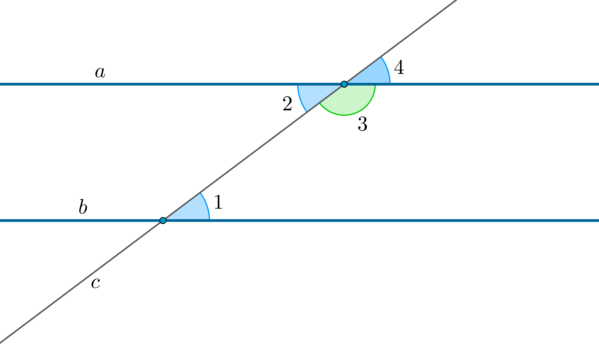
Теоремы: свойства параллельных прямых

1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

 

2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна $180^\circ$.

 

3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.  

$${\Large{\text{Углы треугольника}}}$$

Определения

Треугольник называется остроугольным, если все его углы острые.

 

Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).

 

Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).

 

Теорема

Сумма внутренних углов треугольника равна $180^\circ$.

 

Доказательство

Рассмотрим произвольный треугольник $ABC$ и покажем, что $\angle A + \angle B + \angle C = 180^\circ$.

Проведём через вершину $B$ прямую $a$, параллельную стороне $AC$.

 

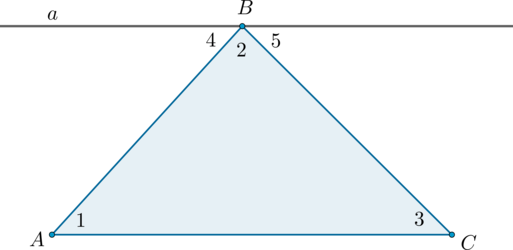
Углы $1$ и $4$ являются накрест лежащими углами при пересечении параллельных прямых $a$ и $AC$ секущей $AB$, а углы $3$ и $5$ – накрест лежащими углами при пересечении тех же параллельных прямых секущей $BC$. Поэтому $$\begin{aligned} &\angle 4 = \angle 1, \ \angle 5 = \angle 3. \qquad \qquad \qquad (1) \end{aligned}$$

Очевидно, сумма углов $4, \ 2$ и $5$ равна развёрнутому углу с вершиной $B$, то есть $\angle 4 + \angle 2 + \angle 5 = 180^\circ$. Отсюда, учитывая равенства $(1)$, получаем: $\angle 1 + \angle 2 + \angle 3 = 180^\circ$.

 

Определение

Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.

 

Теорема

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: $\angle BCD=\angle BAC+\angle ABC$.

 

Доказательство

Рассмотрим рисунок.

 

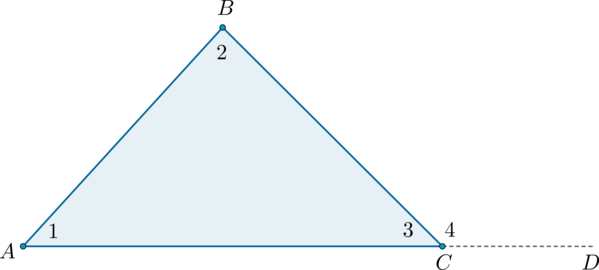
Угол $4$ – внешний угол треугольника, смежный с углом $3$. Так как $\angle 4 + \angle 3 = 180^\circ$, а по теореме о сумме углов треугольника $\angle 1 + \angle 2 + \angle 3 = 180^\circ$, то $\angle 4 = \angle 1 + \angle 2$, что и требовалось доказать.  

$${\Large{\text{Равнобедренный треугольник}}}$$

Определения

Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона - основанием.

 

Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.

 

Теорема

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

 

Доказательство

Пусть $ABC$ – равнобедренный треугольник, $AB = BC$, $BD$ – биссектриса (проведённая к основанию).

Рассмотрим треугольники $ABD$ и $BCD$: $AB = BC$, $\angle ABD = \angle CBD$, $BD$ – общая. Таким образом, $\triangle ABD = \triangle BCD$ по двум сторонам и углу между ними.

Из равенства этих треугольников следует, что $AD = DC$, следовательно, $BD$ – медиана.

 

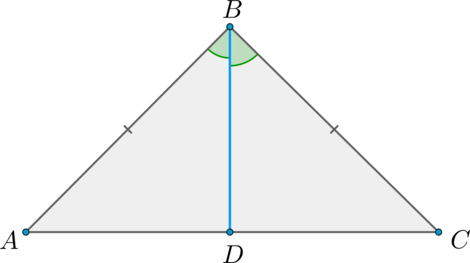
Кроме того, в равных треугольниках против равных сторон лежат равные углы, а $AB = BC$, следовательно, $$\begin{aligned} &\angle ADB = \angle CDB, \qquad \qquad \qquad (2) \end{aligned}$$ но $\angle ADB + \angle CDB = \angle ADC$ – развёрнутый, следовательно, $\angle ADB + \angle CDB = 180^\circ$, откуда при учёте $(2)$: $\angle ADB = 90^\circ = \angle CDB$, то есть $BD$ – высота.

 

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

 

Теорема

В равнобедренном треугольнике углы при основании равны.

 

Доказательство

Проведем биссектрису $BD$ (см. рисунок из предыдущей теоремы). Тогда $\triangle ABD=\triangle CBD$ по первому признаку, следовательно, $\angle A=\angle C$.

 

Теоремы: признаки равнобедренного треугольника

1. Если в треугольнике два угла равны, то треугольник равнобедренный.

 

2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.  

Теорема о соотношении между сторонами и углами треугольника

В треугольнике против большей стороны лежит больший угол.

В треугольнике против большего угла лежит большая сторона.

 

Теорема: неравенство треугольника

В треугольнике сумма любых двух сторон больше третьей стороны.

 

Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.  

$${\Large{\text{Прямоугольный треугольник}}}$$

Определения

В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.

 

Теоремы: свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна $90^\circ$.

 

2. В прямоугольном треугольнике катет, лежащий против угла $30^\circ$, равен половине гипотенузы.

Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла $30^\circ$.