Треугольник. Важные факты о высоте, биссектрисе и медиане

Определения

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

 

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

 

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

 

Теорема

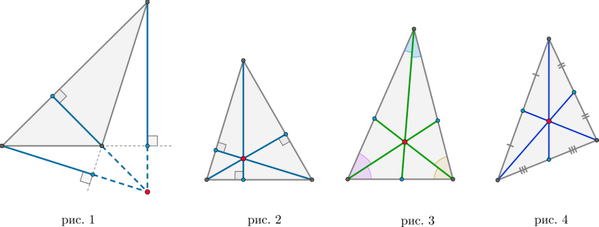
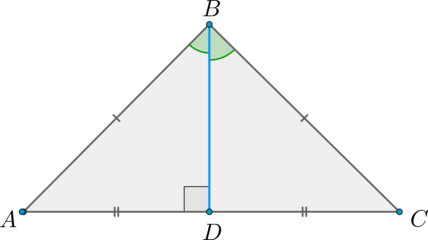
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

Теорема

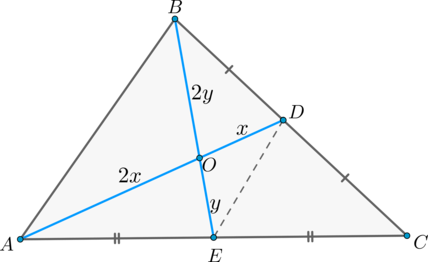
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

 

$${\Large{\text{Медиана}}}$$

Теорема

В любом треугольнике медианы точкой пересечения делятся в отношении $2:1$, считая от вершины.

Доказательство

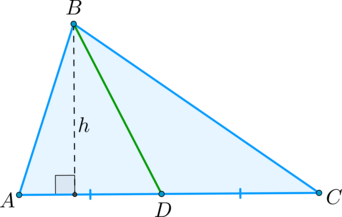
Пусть $AD$ и $BE$ – медианы в треугольнике $ABC$, $O$ – точка пересечения $AD$ и $BE$.

 

$DE$ – средняя линия в треугольнике $ABC$, тогда $DE\parallel AB$, значит $\angle ADE = \angle BAD$, $\angle BED = \angle ABE$, следовательно, треугольники $ABO$ и $DOE$ подобны (по двум углам).

 

Из подобия треугольников $ABO$ и $DOE$: $\dfrac{BO}{OE} = \dfrac{AB}{DE} = \dfrac{2}{1}$.

 

Для других медиан треугольника $ABC$ требуемое свойство доказывается аналогично.

 

Теорема

Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).

 

Доказательство

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию: $S_{ABC} = 0,5\cdot AC\cdot h$.

 

Пусть $BD$ – медиана в треугольнике $ABC$, тогда $AD = DC$.

 

$S_{ABD} = 0,5\cdot AD\cdot h$,

$S_{BCD} = 0,5\cdot DC\cdot h$.

 

Так как $AD = DC$, то $S_{ABD} = S_{BCD}$, что и требовалось доказать.

 

Теорема

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

 

Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.

 

Доказательство

1) Докажем, что если $\triangle ABC$ – прямоугольный, то $BM=\frac12AC$, где $M$ – середина гипотенузы $AC$.

 

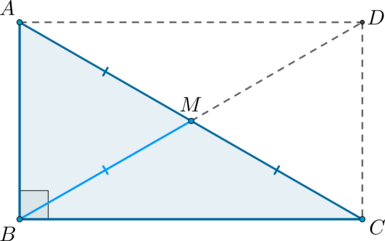
Достроим треугольник $ABC$ до прямоугольника $ABCD$ и проведем диагональ $BD$. Т.к. в прямоугольнике диагонали делятся точкой пересечения пополам и равны, то $AC\cap BD=M$, причем $AM=MC=BM=MD$, чтд.

 

2) Докажем, что если в треугольнике $ABC$ медиана $BM=AM=MC$, то $\angle B=90^\circ$.

 

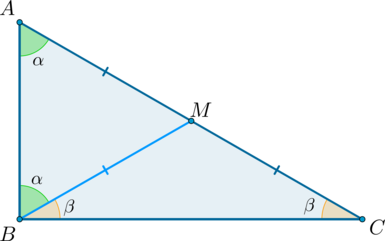
Треугольники $AMB$ и $CMB$ – равнобедренные, следовательно, $\angle BAM=\angle ABM=\alpha, \quad \angle MBC=\angle MCB=\beta$.

 

Т.к. сумма углов в треугольнике равна $180^\circ$, то для $\triangle ABC$:

 

$\alpha+(\alpha+\beta)+\beta=180^\circ \Rightarrow \alpha+\beta=90^\circ \Rightarrow \angle B=90^\circ$, чтд.

 

$${\Large{\text{Биссектриса}}}$$

Теорема

Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:

 

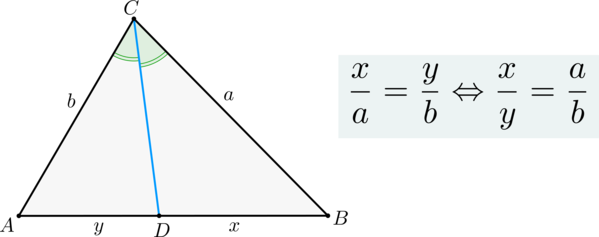
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.

 

Доказательство

Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть $$\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AC\cdot CD}{CB\cdot CD} = \dfrac{AC}{CB}$$

С другой стороны, $\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{0,5\cdot AD\cdot h}{0,5\cdot DB\cdot h}$, где $h$ – высота, проведённая из точки $C$, тогда $\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AD}{DB}$.

 

В итоге $\dfrac{AD}{DB} = \dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AC}{CB}$, откуда $\dfrac{AD}{AC} = \dfrac{DB}{BC}$, что и требовалось доказать.

 

Теорема

Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

 

Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.

 

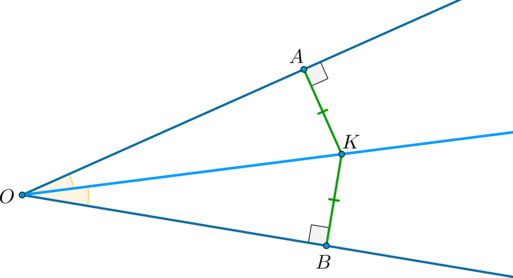
Доказательство

1) Докажем, что если $KA=KB$, то $OK$ – биссектриса.
Рассмотрим треугольники $AOK$ и $BOK$: они равны по катету и гипотенузе, следовательно, $\angle AOK=\angle BOK$, чтд.

 

2) Докажем, что если $OK$ – биссектриса, то $KA=KB$.
Аналогично треугольники $AOK$ и $BOK$ равны по гипотенузе и острому углу, следовательно, $KA=KB$, чтд.