Выпуклый четырехугольник

Определения

Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.

 

Диагональ четырехугольника – отрезок, соединяющий любые две несоседние вершины.

 

Различают выпуклые и невыпуклые четырехугольники.

 

Четырехугольник называется выпуклым, если он находится в одной полуплоскости относительно прямой, содержащей любую его сторону.

 

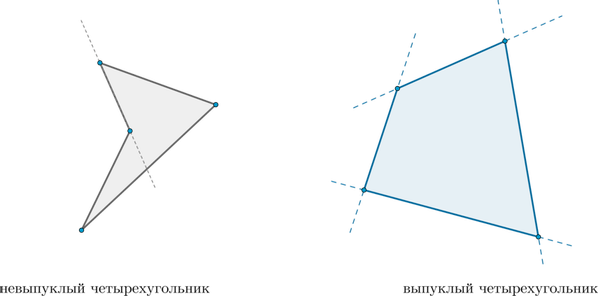
В школьном курсе рассматриваются только выпуклые четырехугольники. Поэтому далее “выпуклый четырехугольник” будем сокращенно называть “четырехугольник”.

 

Теорема

Сумма внутренних углов любого четырехугольника равна $360^\circ$.

 

Доказательство

 

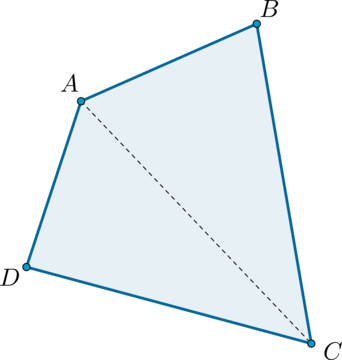
Рассмотрим четырехугольник $ABCD$ и проведем его диагональ $AC$. Она разбила четырехугольник на два треугольника. Сумма углов любого треугольника равна $180^\circ$, следовательно:

$$\begin{multline*} 360^\circ=180^\circ+180^\circ=(\angle DAC+\angle D+\angle ACD) + (\angle CAB+\angle B+\angle ACB)=\\ =\angle D+\angle B +(\angle DAC+\angle CAB)+(\angle ACD+\angle ACB)=\angle D+\angle B+\angle A+\angle C \end{multline*}$$

Теорема Вариньона

Выпуклый четырехугольник, вершинами которого являются середины сторон произвольного четырехугольника, является параллелограммом.

 

Доказательство*
С доказательством данной теоремы рекомендуется ознакомиться после изучения темы “Средняя линия треугольника”.

 

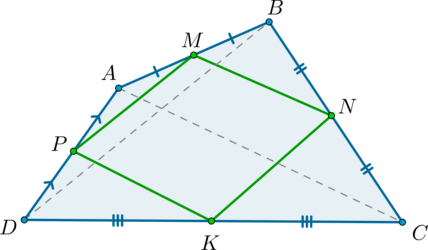
Проведем диагонали четырехугольника $ABCD$. Рассмотрим $\triangle ABC$: $MN$ – средняя линия этого треугольника, следовательно, $MN\parallel AC$.

 

Рассмотрим $\triangle ADC$: $PK$ – средняя линия этого треугольника, следовательно, $PK\parallel AC$.

 

Таким образом, $MN\parallel AC\parallel PK$.

 

Аналогичным образом доказывается, что $MP\parallel BD\parallel NK$.

 

Следовательно, по определению $MNKP$ – параллелограмм.

 

Теорема

Если в четырехугольнике $ABCD$ диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон равны: $$AB^2+CD^2=BC^2+AD^2$$

Доказательство
 

 

 

По теореме Пифагора:

$$\begin{aligned} &AB^2=x^2+a^2\\ &CD^2=b^2+y^2\\ &BC^2=x^2+b^2\\ &AD^2=a^2+y^2 \end{aligned}$$

Из равенств видно, что $AB^2+CD^2=x^2+a^2+y^2+b^2=BC^2+AD^2$

 

Замечание

Все известные четырехугольники, изучаемые в школьной программе, подчиняются следующей схеме:

 

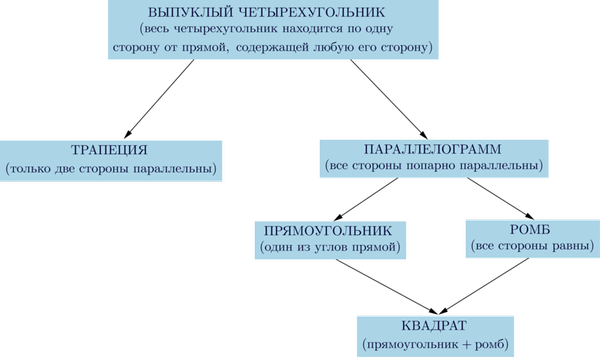
Таким образом, любой четырехугольник из этой схемы обладает свойствами всех предыдущих четырехугольников, из которых он следует.

 

Например, прямоугольник обладает свойствами параллелограмма и произвольного выпуклого четырехугольника; квадрат обладает свойствами прямоугольника, параллелограмма, выпуклого четырехугольника.