Правильный шестиугольник и его свойства

Определение

Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.

 

Замечание

Т.к. сумма всех углов $n$–угольника равна $180^\circ(n-2)$, то каждый угол правильного $n$–угольника равен $$\alpha_n=\dfrac{n-2}n \cdot 180^\circ$$

Пример

Каждый угол правильного четырехугольника (т.е. квадрата) равен $\dfrac {4-2}4\cdot 180^\circ=90^\circ$;

 

каждый угол правильного шестиугольника равен $\dfrac{6-2}6\cdot 180^\circ=120^\circ$.

 

Теоремы

1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

 

2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

 

Следствия

1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.

 

2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.

 

Теорема

Если $a$ – сторона правильного $n$–угольника, $R$ и $r$ – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: $$\begin{aligned} S&=\dfrac n2ar\\ a&=2R\cdot \sin\dfrac{180^\circ}n\\ r&=R\cdot \cos\dfrac{180^\circ}n \end{aligned}$$

 

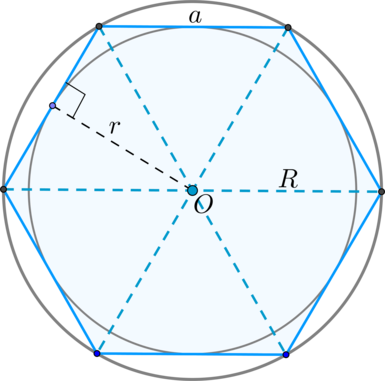
Свойства правильного шестиугольника

1. Сторона равна радиусу описанной окружности: $a=R$.

2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.

3. Все углы правильного шестиугольника равны $120^\circ$.

4. Площадь правильного шестиугольника со стороной $a$ равна $\dfrac{3\sqrt{3}}{2}a^2$.

5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу $r$ вписанной в правильный шестиугольник окружности.

6. Инвариантен относительно поворота плоскости на угол, кратный $60^\circ$ относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).

 

Замечание

В общем случае правильный $n$-угольник инвариантен относительно поворота на угол $\dfrac{360^\circ}{n}$.