Площади многоугольников

$${\Large{\text{Основные факты о площади}}}$$

Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник. За единицу измерения площади принимают площадь квадрата со стороной $1$ см, $1$ мм и т.д. (единичный квадрат). Тогда площадь будет измеряться в см$^2$, мм$^2$ соответственно.

Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.

 

Свойства площади

1. Площадь любого многоугольника — величина положительная.

2. Равные многоугольники имеют равные площади.

3. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

4. Площадь квадрата со стороной $a$ равна $a^2$.  

$${\Large{\text{Площадь прямоугольника и параллелограмма}}}$$

Теорема: площадь прямоугольника

Площадь прямоугольника со сторонами $a$ и $b$ равна $S=ab$.

 

Доказательство

Достроим прямоугольник $ABCD$ до квадрата со стороной $a+b$, как показано на рисунке:

 

Данный квадрат состоит из прямоугольника $ABCD$, еще одного равного ему прямоугольника и двух квадратов со сторонами $a$ и $b$. Таким образом,

 

$\begin{multline*} S_{a+b}=2S_{\text{пр-к}}+S_a+S_b \Leftrightarrow (a+b)^2=2S_{\text{пр-к}}+a^2+b^2 \Leftrightarrow\\ a^2+2ab+b^2=2S_{\text{пр-к}}+a^2+b^2 \Rightarrow S_{\text{пр-к}}=ab \end{multline*}$

 

Определение

Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота $BK$ падает на сторону $AD$, а высота $BH$ — на продолжение стороны $CD$:

 

Теорема: площадь параллелограмма

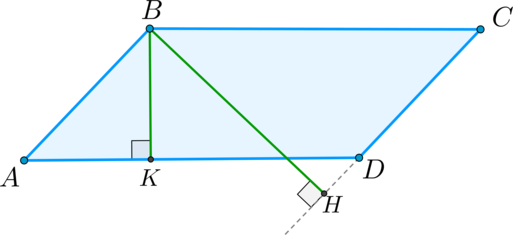
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.

 

Доказательство

Проведем перпендикуляры $AB'$ и $DC'$, как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма $ABCD$.

 

Тогда $AB'C'D$ – прямоугольник, следовательно, $S_{AB'C'D}=AB'\cdot AD$.

 

Заметим, что прямоугольные треугольники $ABB'$ и $DCC'$ равны. Таким образом,

 

$S_{ABCD}=S_{ABC'D}+S_{DCC'}=S_{ABC'D}+S_{ABB'}=S_{AB'C'D}=AB'\cdot AD.$

 

$${\Large{\text{Площадь треугольника}}}$$

Определение

Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.

 

Теорема

Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.

 

Доказательство

Пусть $S$ – площадь треугольника $ABC$. Примем сторону $AB$ за основание треугольника и проведём высоту $CH$. Докажем, что $$S = \dfrac{1}{2}AB\cdot CH.$$ Достроим треугольник $ABC$ до параллелограмма $ABDC$ так, как показано на рисунке:



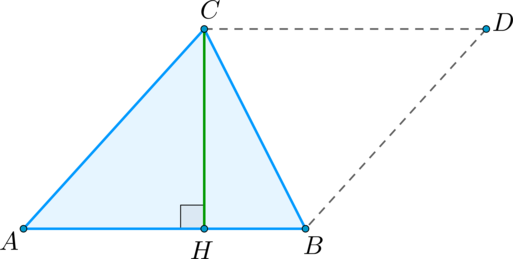
Треугольники $ABC$ и $DCB$ равны по трем сторонам ($BC$ – их общая сторона, $AB = CD$ и $AC = BD$ как противоположные стороны параллелограмма $ABDC$), поэтому их площади равны. Следовательно, площадь $S$ треугольника $ABC$ равна половине площади параллелограмма $ABDC$, то есть $S = \dfrac{1}{2}AB\cdot CH$.

 

Теорема

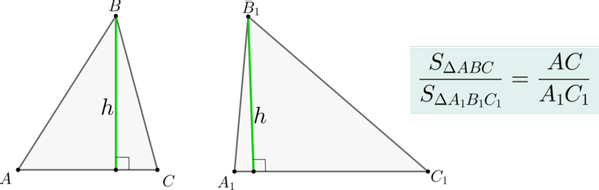
Если два треугольника $\triangle ABC$ и $\triangle A_1B_1C_1$ имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.

 

Следствие

Медиана треугольника делит его на два треугольника, равных по площади.

 

Теорема

Если два треугольника $\triangle ABC$ и $\triangle A_2B_2C_2$ имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.

 

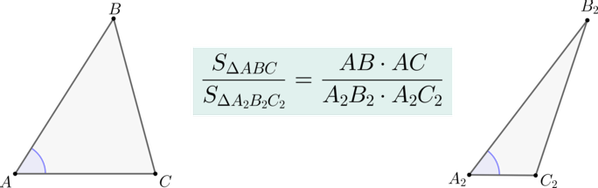
Доказательство

Пусть $\angle A=\angle A_2$. Совместим эти углы так, как показано на рисунке (точка $A$ совместилась с точкой $A_2$):

 

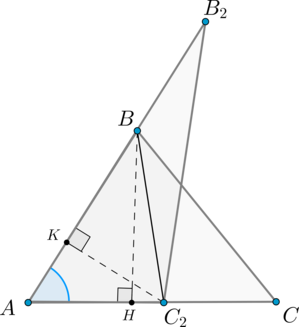
Проведем высоты $BH$ и $C_2K$.

Треугольники $AB_2C_2$ и $ABC_2$ имеют одинаковую высоту $C_2K$, следовательно: $$\dfrac{S_{AB_2C_2}}{S_{ABC_2}}=\dfrac{AB_2}{AB}$$

Треугольники $ABC_2$ и $ABC$ имеют одинаковую высоту $BH$, следовательно: $$\dfrac{S_{ABC_2}}{S_{ABC}}=\dfrac{AC_2}{AC}$$

Перемножая последние два равенства, получим: $$\dfrac{S_{AB_2C_2}}{S_{ABC}}=\dfrac{AB_2\cdot AC_2}{AB\cdot AC} \qquad \text{ или } \qquad \dfrac{S_{A_2B_2C_2}}{S_{ABC}}=\dfrac{A_2B_2\cdot A_2C_2}{AB\cdot AC}$$

Теорема Пифагора

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:

 

Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.

 

Теорема

Площадь прямоугольного треугольника равна половине произведения катетов.

 

Теорема: формула Герона

Пусть $p$ – полупериметр треугольника, $a$, $b$, $c$ – длины его сторон, тогда его площадь равна $$S_{\triangle}=\sqrt{p(p - a)(p - b)(p - c)}$$

 

$${\Large{\text{Площадь ромба и трапеции}}}$$

Замечание

Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.

 

Теорема

Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.

 

Доказательство

Рассмотрим четырехугольник $ABCD$. Обозначим $AO=a, CO=b, BO=x, DO=y$:

 

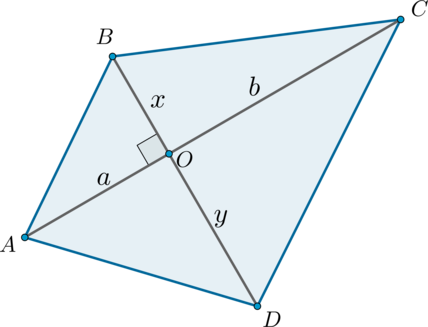
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:

$\begin{multline*} S_{ABCD}=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\ \frac12((a+b)x+(a+b)y)=\frac12(a+b)(x+y)\end{multline*}$

Следствие: площадь ромба

Площадь ромба равна половине произведения его диагоналей: $$S_{\text{ромб}}=\dfrac12 d_1\cdot d_2$$

Определение

Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.

 

Теорема: площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

 

Доказательство

Рассмотрим трапецию $ABCD$ с основаниями $BC$ и $AD$. Проведем $CD'\parallel AB$, как показано на рисунке:

 

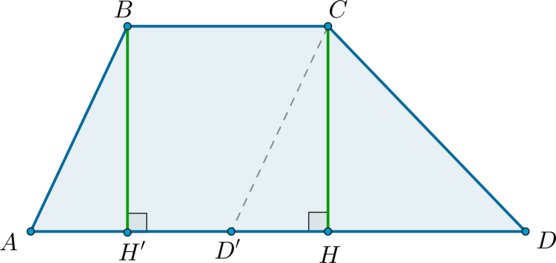
Тогда $ABCD'$ – параллелограмм.

 

Проведем также $BH'\perp AD, CH\perp AD$ ($BH'=CH$ – высоты трапеции).

 

Тогда $S_{ABCD'}=BH'\cdot AD'=BH'\cdot BC, \quad S_{CDD'}=\dfrac12CH\cdot D'D$

 

Т.к. трапеция состоит из параллелограмма $ABCD'$ и треугольника $CDD'$, то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:

$$S_{ABCD}=S_{ABCD'}+S_{CDD'}=BH'\cdot BC+\dfrac12CH\cdot D'D=\dfrac12CH\left(2BC+D'D\right)=$$ $$=\dfrac12 CH\left(BC+AD'+D'D\right)=\dfrac12 CH\left(BC+AD\right)$$