Начальные сведения о синусе, косинусе, тангенсе и котангенсе

Определения

Синус острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к гипотенузе: $\sin \alpha=\dfrac ac$

 

Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к гипотенузе: $\cos \alpha=\dfrac bc$

 

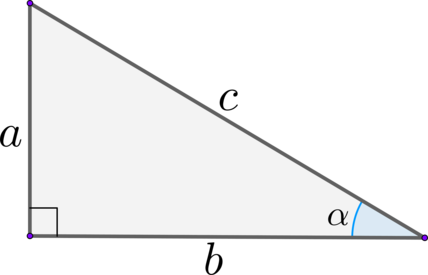
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к прилежащему катету: $\mathrm{tg}\,\alpha=\dfrac ab$

 

Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к противолежащему катету: $\mathrm{ctg}\,\alpha=\dfrac ba$

 

Утверждение

Синусы, косинусы, тангенсы и котангенсы равных углов соответственно равны.

 

Теорема

Из определений синуса, косинуса, тангенса и котангенса вытекают следующие формулы:

$${\large{\begin{array}{|lcl|} \hline &&\\ \sin^2 \alpha+\cos^2 \alpha =1&\qquad& \mathrm{tg}\, \alpha \cdot \mathrm{ctg}\, \alpha =1\\ &&\\ \mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos \alpha}&&\mathrm{ctg}\, \alpha =\dfrac{\cos \alpha}{\sin \alpha}\\&&\\ \hline \end{array}}}$$

Утверждение

В прямоугольном треугольнике $ABC$ с прямым углом $\angle C$:

 

$\sin \angle A=\cos \angle B$

 

$\mathrm{tg}\,\angle A=\mathrm{ctg}\,\angle B$

 

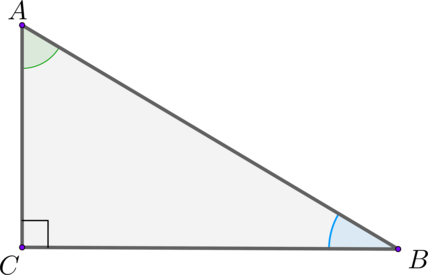
Доказательство

Утверждение следует непосредственно из определения синуса и косинуса острого угла в прямоугольном треугольнике.

 

Теорема

Для углов $30^\circ, 45^\circ, 60^\circ$ верна следующая таблица:

$${\large{\begin{array}{|c|c|c|c|} \hline & \phantom{000}30^\circ \phantom{000} & \phantom{000} 45^\circ \phantom{000} & \phantom{000} 60^\circ \phantom{000} \\[2pt] \hline &&&\\ \sin &\frac12&\frac{\sqrt2}2&\frac{\sqrt3}2\\[4pt] \cos &\frac{\sqrt3}2&\frac{\sqrt2}2&\frac12\\[4pt] \mathrm{tg} &\frac{\sqrt3}3&1&\sqrt3\\[4pt] \mathrm{ctg}&\sqrt3&1&\frac{\sqrt3}3\\[4pt] \hline \end{array}}}$$

Доказательство

1) Рассмотрим прямоугольный треугольник $ABC$: $\angle C=90^\circ, \angle A=60^\circ, \angle B=30^\circ$.

 

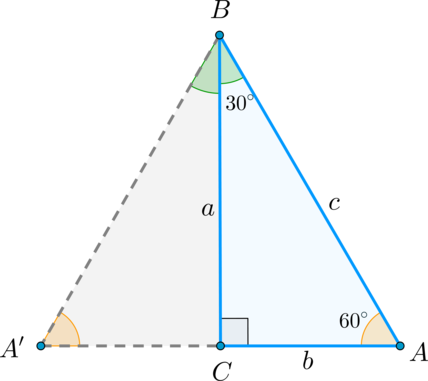
На стороне $BC$ построим равный ему треугольник $A'BC$, как показано на рисунке.

Полученный треугольник $A'BA$ является правильным, т.к. $\angle A'=\angle A=\angle A'BA=60^\circ$.
Следовательно, $A'A=2b=AB=c$, откуда $b=\dfrac12c$.

Тогда по теореме Пифагора $a^2+b^2=c^2 \Rightarrow a=\dfrac{\sqrt3}2c$.

Теперь по определению $\sin \angle A=\sin 60^\circ =\dfrac ac=\dfrac{\sqrt3}2$

Т.к. по предыдущему утверждению $\sin \angle A=\cos \angle B$, то $\cos 30^\circ =\dfrac{\sqrt3}2$.

Т.к. $\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}$, то $\mathrm{tg}\,30^\circ=\mathrm{ctg}\,60^\circ=\dfrac{\sqrt3}3$, а $\mathrm{tg}\,60^\circ=\mathrm{ctg}\,30^\circ=\sqrt3$.

 

2) Рассмотрим прямоугольный треугольник $ABC$: $\angle C=90^\circ, \angle A=45^\circ, \angle B=45^\circ$.

 

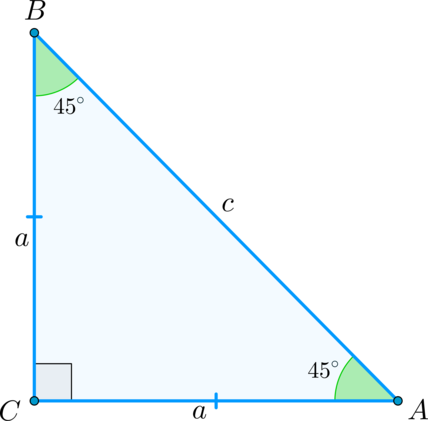
Этот треугольник равнобедренный, следовательно, $BC=AC=a$.

Тогда по теореме Пифагора $a^2+a^2=c^2 \Rightarrow a=\dfrac{\sqrt2}2c$.

Следовательно, $\sin \angle A=\cos\angle A=\sin\angle B=\cos \angle B=\dfrac{\sqrt2}2$.

Из определения следует, что $\mathrm{tg}\,45^\circ=\mathrm{ctg}\,45^\circ=1$.

 

Замечание

Для простоты запоминания таблицы можно записать ее в следующем виде:

$${\large{\begin{array}{|c|c|c|c|} \hline & \phantom{000}30^\circ \phantom{000} & \phantom{000} 45^\circ \phantom{000} & \phantom{000} 60^\circ \phantom{000} \\[2pt] \hline &&&\\ \sin &\frac{\sqrt1}2&\frac{\sqrt2}2&\frac{\sqrt3}2\\[4pt] \cos &\frac{\sqrt3}2&\frac{\sqrt2}2&\frac{\sqrt1}2\\[4pt] \mathrm{tg} &\frac1{\sqrt3}&1&\sqrt3\\[4pt] \mathrm{ctg}&\sqrt3&1&\frac1{\sqrt3}\\[4pt] \hline \end{array}}}$$

То есть для синуса и косинуса число выглядит как $\dfrac{\sqrt{\phantom{0}}}2$, где у синуса под корнем пишется $1, 2, 3$, у косинуса – наоборот.

 

$${\Large{\text{Синус, косинус, тангенс и котангенс тупого угла}}}$$

Теорема

Справедливы следующие формулы приведения:

$$\begin{aligned} \sin(180^\circ-\alpha)&=\sin\alpha\\ \cos(180^\circ-\alpha)&=-\cos\alpha\\ \mathrm{tg}\,(180^\circ-\alpha)&=-\mathrm{tg}\,\alpha\\ \mathrm{ctg}\,(180^\circ-\alpha)&=-\mathrm{ctg}\,\alpha \end{aligned}$$

Таким образом, если $\alpha$ – острый угол, то с помощью этих формул можно найти синус, косинус, тангенс или котангенс тупого угла, смежного с $\alpha$.

 

Пример

$\sin 135^\circ=\sin(180^\circ-45^\circ)=\sin45^\circ=\dfrac{\sqrt2}2$