Справочник с основными фактами стереометрии

Факт 1. Про параллельность прямыхФакт 1. Про параллельность прямых
∙∙ Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
∙∙ Через две параллельные прямые проходит плоскость, и притом только одна.
∙∙ Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
∙∙ Если прямая aa параллельна прямой bb, а та в свою очередь параллельна прямой cc, то a∥ca∥c.
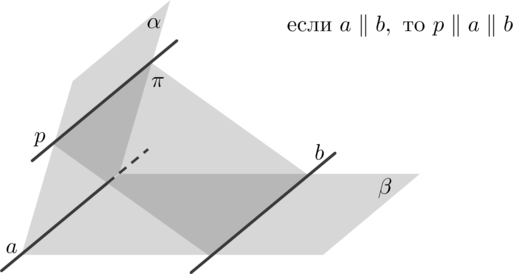
∙∙ Пусть плоскости αα и ββ пересекаются по прямой aa, плоскости ββ и ππ пересекаются по прямой bb, плоскости ππ и αα пересекаются по прямой pp. Тогда если a∥ba∥b, то p∥ap∥a (или p∥bp∥b):

Факт 2. Про параллельность прямой и плоскостиФакт 2. Про параллельность прямой и плоскости
∙∙ Существует три вида взаимного расположения прямой и плоскости:
1. прямая имеет с плоскостью две общие точки (то есть лежит в плоскости);
2. прямая имеет с плоскостью ровно одну общую точку (то есть пересекает плоскость);
3. прямая не имеет с плоскостью общих точек (то есть параллельна плоскости).
∙∙ Если прямая aa, не лежащая в плоскости ππ, параллельна некоторой прямой pp, лежащей в плоскости ππ, то она параллельна данной плоскости.



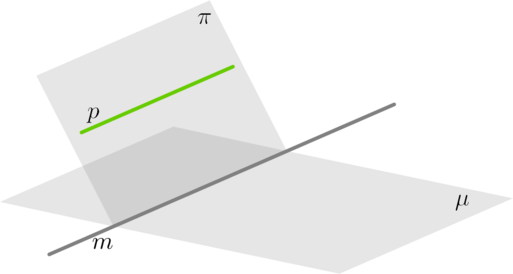
∙∙ Пусть прямая pp параллельна плоскости μμ. Если плоскость ππ проходит через прямую pp и пересекает плоскость μμ, то линия пересечения плоскостей ππ и μμ — прямая mm — параллельна прямой pp.

Факт 3. Про параллельность плоскостейФакт 3. Про параллельность плоскостей
∙∙ Если две плоскости не имеют общих точек, то они называются параллельными плоскостями.
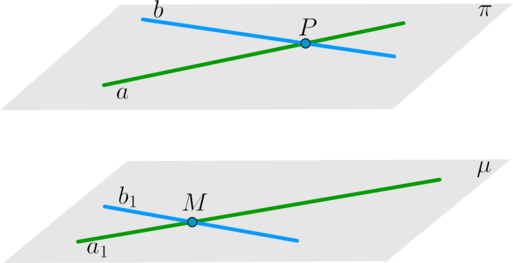
∙∙ Если две пересекающиеся прямые из одной плоскости соответственно параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.



∙∙ Если две параллельные плоскости αα и ββ пересечены третьей плоскостью γγ, то линии пересечения плоскостей также параллельны: α∥β, α∩γ=a, β∩γ=b⟹a∥bα∥β, α∩γ=a, β∩γ=b⟹a∥b


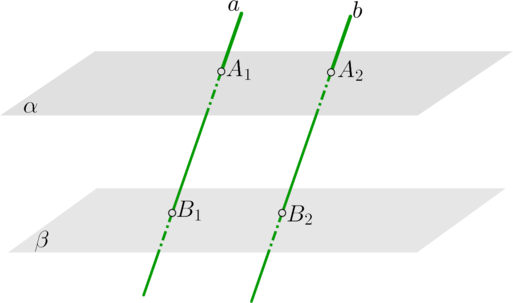
∙∙ Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны: α∥β, a∥b⟹A1B1=A2B2α∥β, a∥b⟹A1B1=A2B2

Факт 4. Про скрещивающиеся прямыеФакт 4. Про скрещивающиеся прямые
∙∙ Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
∙∙ Признак:
Пусть прямая ll лежит в плоскости λλ. Если прямая ss пересекает плоскость λλ в точке SS, не лежащей на прямой ll, то прямые ll и ss скрещиваются.



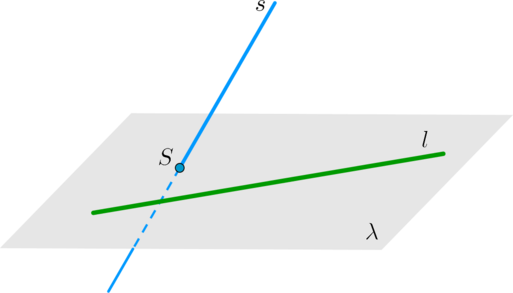
∙∙ алгоритм нахождения угла между скрещивающимися прямыми aa и bb:
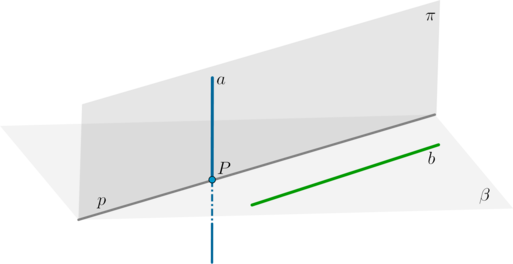
Шаг 1. Через одну из двух скрещивающихся прямых aa провести плоскость ππ параллельно другой прямой bb. Как это сделать: проведем плоскость ββ через прямую bb так, чтобы она пересекала прямую aa в точке PP; через точку PP проведем прямую p∥bp∥b; тогда плоскость, проходящая через aa и pp, и есть плоскость ππ.
Шаг 2. В плоскости ππ найти угол между прямыми aa и pp (p∥bp∥b). Угол между ними будет равен углу между скрещивающимися прямыми aa и bb.

Факт 5. Про перпендикулярность прямой и плоскостиФакт 5. Про перпендикулярность прямой и плоскости
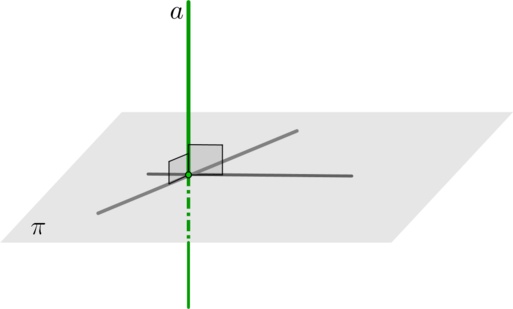
∙∙ Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
∙∙ Если две прямые перпендикулярны плоскости, то они параллельны.
∙∙ Признак: если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

Факт 6. Про расстоянияФакт 6. Про расстояния
∙∙ Для того, чтобы найти расстояние между параллельными прямыми, нужно из любой точки одной прямой опустить перпендикуляр на другую прямую. Длина перпендикуляра и есть расстояние между этими прямыми.
∙∙ Для того, чтобы найти расстояние между плоскостью и параллельной ей прямой, нужно из любой точки прямой опустить перпендикуляр на эту плоскость. Длина перпендикуляра и есть расстояние между этими прямой и плоскостью.
∙∙ Для того, чтобы найти расстояние между параллельными плоскостями, нужно из любой точки одной плоскости опустить перпендикуляр к другой плоскости. Длина этого перпендикуляра и есть расстояние между параллельными плоскостями.
∙∙ алгоритм нахождения расстояния между скрещивающимися прямыми aa и bb:
Шаг 1. Через одну из двух скрещивающихся прямых aa провести плоскость ππ параллельно другой прямой bb. Как это сделать: проведем плоскость ββ через прямую bb так, чтобы она пересекала прямую aa в точке PP; через точку PP проведем прямую p∥bp∥b; тогда плоскость, проходящая через aa и pp, и есть плоскость ππ.
Шаг 2. Найдите расстояние от любой точки прямой bb до плоскости ππ. Это расстояние и есть расстояние между скрещивающимися прямыми aa и bb.  

Факт 7. Про теорему о трех перпендикулярах (ТТП)Факт 7. Про теорему о трех перпендикулярах (ТТП)
∙∙ Пусть AHAH – перпендикуляр к плоскости ββ. Пусть AB,BHAB,BH – наклонная и ее проекция на плоскость ββ. Тогда прямая xx в плоскости ββ будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции: 1.AH⊥β, AB⊥x⇒BH⊥x2.AH⊥β, BH⊥x⇒AB⊥x1.AH⊥β, AB⊥x⇒BH⊥x2.AH⊥β, BH⊥x⇒AB⊥x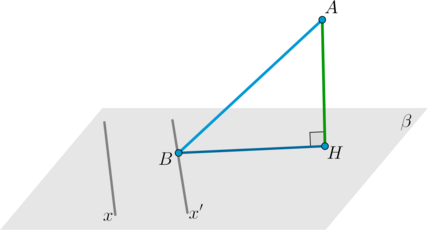

Заметим, что прямая xx необязательно должна проходить через точку BB. Если она не проходит через точку BB, то строится прямая x′x′, проходящая через точку BB и параллельная xx. Если, например, x′⊥BHx′⊥BH, то и x⊥BHx⊥BH.  

Факт 8. Про угол между прямой и плоскостью, а также угол между плоскостямиФакт 8. Про угол между прямой и плоскостью,а также угол между плоскостями
∙∙ Угол между наклонной прямой и плоскостью — это угол между этой прямой и ее проекцией на данную плоскость. Таким образом, данный угол принимает значения из промежутка (0∘;90∘)(0∘;90∘).
Если прямая лежит в плоскости, то угол между ними считается равным 0∘0∘. Если прямая перпендикулярна плоскости, то, исходя из определения, угол между ними равен 90∘90∘.
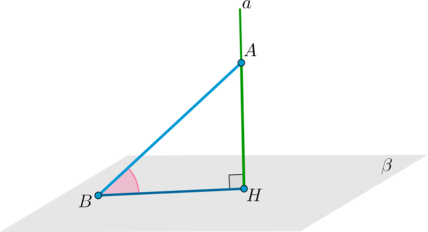
∙∙ Чтобы найти угол между наклонной прямой и плоскостью, необходимо отметить некоторую точку AA на этой прямой и провести перпендикуляр AHAH к плоскости. Если BB – точка пересечения прямой с плоскостью, то ∠ABH∠ABH и есть искомый угол.



∙∙ Для того, чтобы найти угол между плоскостями αα и ββ, можно действовать по следующему алгоритму:
Отметить произвольную точку AA в плоскости αα.
Провести AH⊥hAH⊥h, где hh — линия пересечения плоскостей.
Провести ABAB перпендикулярно плоскости ββ.
Тогда ABAB – перпендикуляр к плоскости ββ, AHAH – наклонная, следовательно, HBHB – проекция. Тогда по ТТП HB⊥hHB⊥h.
Следовательно, ∠AHB∠AHB — линейный угол двугранного угла между плоскостями. Градусная мера этого угла и есть градусная мера угла между плоскостями.



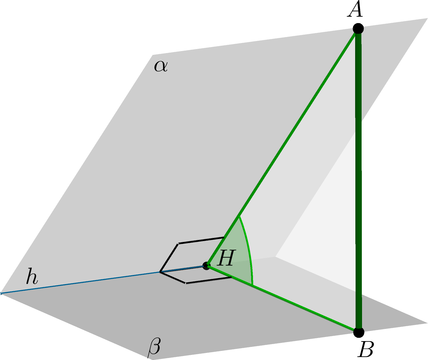
Заметим, что мы получили прямоугольный треугольник △AHB△AHB (∠B=90∘∠B=90∘). Как правило, находить ∠AHB∠AHB удобно из него.  

Факт 9. Про перпендикулярность плоскостейФакт 9. Про перпендикулярность плоскостей
∙∙ Признак: если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости. a⊥β, a∈α⇒α⊥βa⊥β, a∈α⇒α⊥β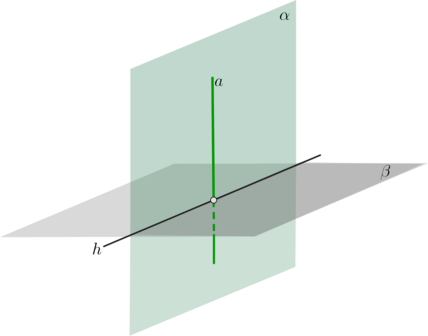

∙∙ Заметим, что так как через прямую aa можно провести бесконечное множество плоскостей, то существует бесконечное множество плоскостей, перпендикулярных ββ (и проходящих через aa).