Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми

${\color{red}{\textbf{Факт 1. Про векторы}}}$
$\bullet$ Если в пространстве заданы две точки $A(x_1;y_1;z_1)$ и $B(x_2;y_2;z_2)$, то вектор $\overrightarrow{AB}$ имеет координаты $$\overrightarrow{AB} = \{x_2-x_1;y_2-y_1;z_2-z_1\}$$
$\bullet$ Если в пространстве заданы два вектора $\vec{a} =\{x_1;y_1;z_1\}$ и $\vec{b}= \{x_2;y_2;z_2\}$, то:

$\qquad \blacktriangleright$ сумма этих векторов $\vec{a}+\vec{b}=\{x_1+x_2;y_1+y_2;z_1+z_2\}$

$\qquad \blacktriangleright$ разность этих векторов $\vec{a}-\vec{b}=\{x_1-x_2;y_1-y_2;z_1-z_2\}$

$\qquad \blacktriangleright$ произведение вектора на число $\lambda \vec{a}=\{\lambda x_1;\lambda y_1;\lambda z_1\}$   $\bullet$ Если в пространстве заданы две точки $A(x_1;y_1;z_1)$ и $B(x_2;y_2;z_2)$, а точка $O$ — середина отрезка $AB$, то $O$ имеет координаты $$O\left(\dfrac{x_1+x_2}2;\dfrac{y_1+y_2}2;\dfrac{z_1+z_2}2\right)$$
$\bullet$ Длина вектора $\vec{a}=\{x;y;z\}$ обозначается $|\vec{a}|$ и вычисляется по формуле $$|\vec{a}|=\sqrt{x^2+y^2+z^2}$$
$\bullet$ Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.  

${\color{red}{\textbf{Факт 2. Про скалярное произведение}}}$
$\bullet$ Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: $${\large{(\vec{a}, \vec{b})=|\vec{a}|\cdot|\vec{b}|\cdot\cos \angle (\vec{a}, \vec{b})}}$$ На рисунке показано, что такое угол между векторами:



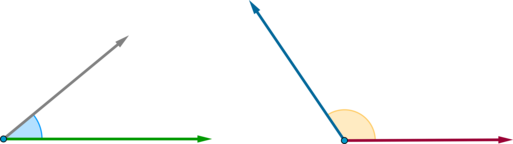
$\bullet$ Справедливы следующие утверждения:

I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: $$(\vec{a}, \vec{b})=0 \quad\Leftrightarrow\quad \vec{a}\perp \vec{b}$$

II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: $$|\vec{a}|=\sqrt{(\vec{a}, \vec{a})}$$

III. Переместительный закон: $$(\vec{a}, \vec{b})=(\vec{b}, \vec{a})$$

IV. Распределительный закон: $$(\vec{a}+\vec{b}, \vec{c})=(\vec{a}, \vec{c})+(\vec{b}, \vec{c})$$

V. Сочетательный закон ($\lambda$ – число): $$\lambda(\vec{a}, \vec{b})=(\lambda \vec{a}, \vec{b})$$
$\bullet$ Скалярное произведение двух векторов $\vec{a} =\{x_1;y_1;z_1\}$ и $\vec{b}= \{x_2;y_2;z_2\}$ можно вычислить с помощью координат этих векторов: $${\large{(\vec{a}, \vec{b})=x_1x_2+y_1y_2+z_1z_2}}$$
$\bullet$ Косинус угла между векторами $\vec{a} =\{x_1;y_1;z_1\}$ и $\vec{b}= \{x_2;y_2;z_2\}$ вычисляется по формуле: $${\large{\cos\angle(\vec{a}, \vec{b})=\dfrac{x_1x_2+y_1y_2+z_1z_2} {\sqrt{x^2_1+y^2_1+z^2_1}\cdot \sqrt{x^2_2+y^2_2+z^2_2}}}}$$  

${\color{red}{\textbf{Факт 3. Про уравнение плоскости}}}$
$\bullet$ Если $\vec{n}=\{a;b;c\}$ – нормаль к плоскости, то уравнение плоскости имеет вид $$ax+by+cz+d=0$$ Для того, чтобы найти $d$, нужно подставить в уравнение плоскости вместо $x, y, z$ координаты любой точки, лежащей в этой плоскости.   Пример: если $\vec{n}=\{1;2;3\}$ – нормаль к плоскости, $O(4;5;6)$ – точка из плоскости, то справедливо: $1\cdot 4+2\cdot 5+3\cdot 6+d=0$, откуда $d=-32$, следовательно, уравнение плоскости имеет вид $x+2y+3z-32=0$.   $\bullet$ Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть $A(1;0;0), \ B(0;3;4), \ C(2;0;5)$ – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: $$\begin{cases} 1\cdot a+0\cdot b+0\cdot c+d=0\\ 0\cdot a+3\cdot b+4\cdot c+d=0\\ 2\cdot a+0\cdot b+5\cdot c+d=0\end{cases} \quad\Rightarrow\quad \begin{cases} d=-a\\ 3b+4c-a=0\\ a+5c=0\end{cases}\quad\Rightarrow\quad \begin{cases} d=-a\\ a=-5c\\ b=-3c\end{cases}\quad\Rightarrow\quad\begin{cases}a=-5c\\ b=-3c\\ d=5c\end{cases}$$ Следовательно, уравнение плоскости имеет вид: $$-5c\cdot x-3c\cdot y+c\cdot z+5c=0$$ Можно разделить обе части на $c$, так как $c\ne 0$ (иначе $a=b=c=d=0$), следовательно, уравнение плоскости имеет вид $$-5x-3y+z+5=0$$  

${\color{red}{\textbf{Факт 4. Про углы между прямыми, плоскостями}}}$
$\bullet$ Если векторы $\vec{a} =\{x_1;y_1;z_1\}$ и $\vec{b}= \{x_2;y_2;z_2\}$ являются направляющими прямых $p$ и $q$, то косинус угла между этими прямыми равен: $$\cos \phi=\dfrac{|x_1x_2+y_1y_2+z_1z_2|} {\sqrt{x^2_1+y^2_1+z^2_1}\cdot \sqrt{x^2_2+y^2_2+z^2_2}}$$
$\bullet$ Если $\vec{a}$ — направляющий вектор прямой $p$, а $\vec{n}$ — нормаль к плоскости $\phi$ (перпендикуляр к плоскости), то синус угла между прямой $p$ и плоскостью $\phi$ равен модулю косинуса угла между векторами $\vec{a}$ и $\vec{n}$: $$\sin \angle(p, \phi)=|\cos \angle(\vec{a}, \vec{n})|$$   $\bullet$ Если две плоскости заданы уравнениями $a_1x+b_1y+c_1z+d_1=0$ и $a_2x+b_2y+c_2z+d_2=0$, то косинус угла между плоскостями ищется по формуле: $${\large{\cos \phi=\left| \dfrac{a_1a_2+b_1b_2+c_1c_2} {\sqrt{a^2_1+b^2_1+c^2_1}\cdot \sqrt{a^2_2+b^2_2+c^2_2}}\right|}}$$  

${\color{red}{\textbf{Факт 5. Про расстояния от точки до плоскости, между скрещивающимися прямыми}}}$
$\bullet$ Если $M(x_0;y_0;z_0)$ — некоторая точка вне плоскости $\phi$, $ax+by+cz+d=0$ — уравнение плоскости $\phi$, то расстояние от точки $M$ до плоскости $\phi$ ищется по формуле: $$\rho(M, \phi)=\dfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$$
$\bullet$ Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.