Производная. Таблица производных. Связь функции и производной. Касательная. Первообразная
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#539
Факт 1.
Таблица производных:
Факт 2.
Пусть – функции.
Если
– число, то:
Производная суммы/разности двух функций:
Производная произведения двух функций:
Производная частного двух функций:
Производная сложной функции:
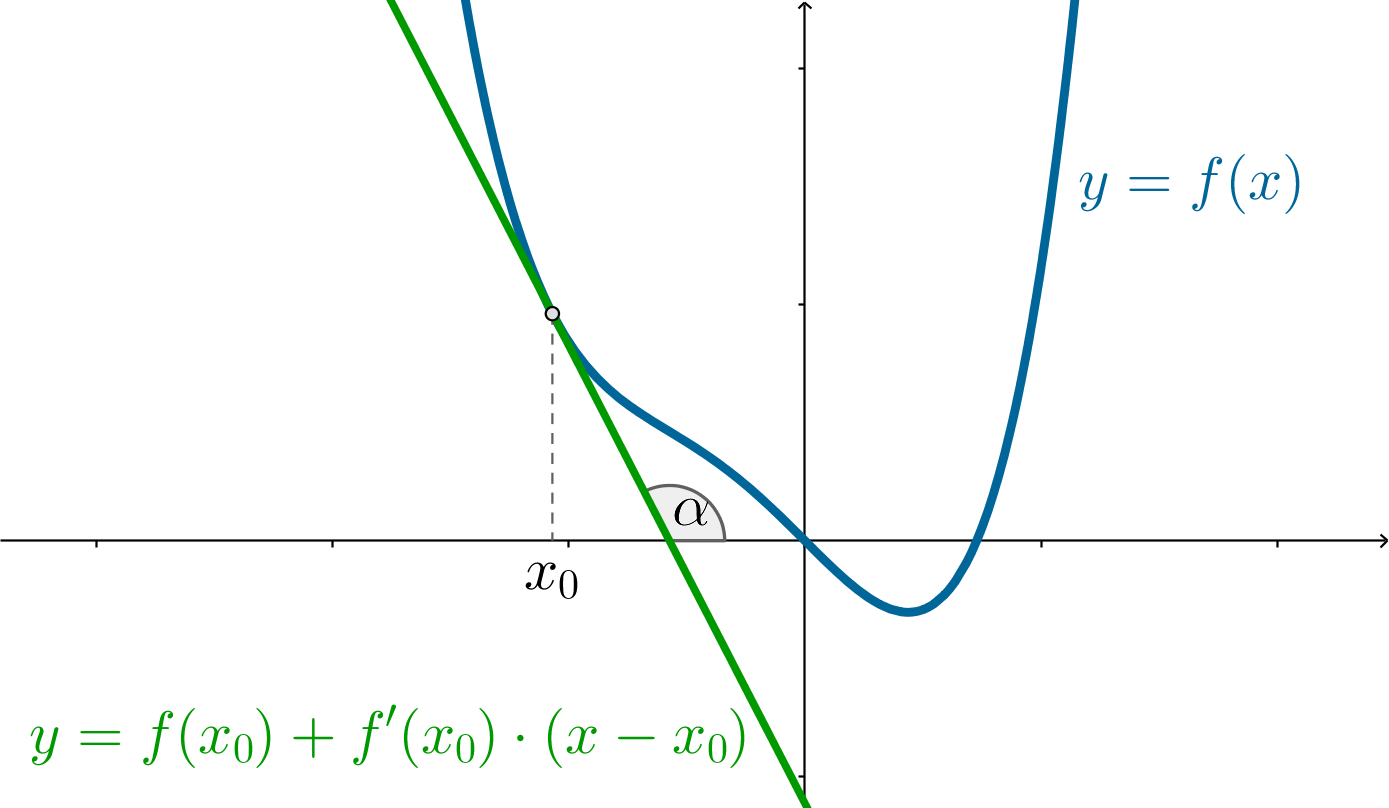
Факт 3. Если
– некоторая функция, то касательная к ней в точке с абсциссой
имеет вид:
Следовательно,
– тангенс угла наклона касательной к
положительному направлению оси
, он же угловой коэффициент касательной,
если ее уравнение записать как
.
Факт 4. Если
на
, то
возрастает на
.
Если
на
, то
убывает на
.
Если
и в точке
производная меняет свой знак, то
—
экстремум функции
:
— если производная меняет знак с “” на “
” (считая слева направо), то
—
минимум;
— если производная меняет знак с “” на “
” (считая слева направо), то
—
максимум.
Факт 5.
– первообразная для
, если
.
Обозначение:
где – некоторая константа.
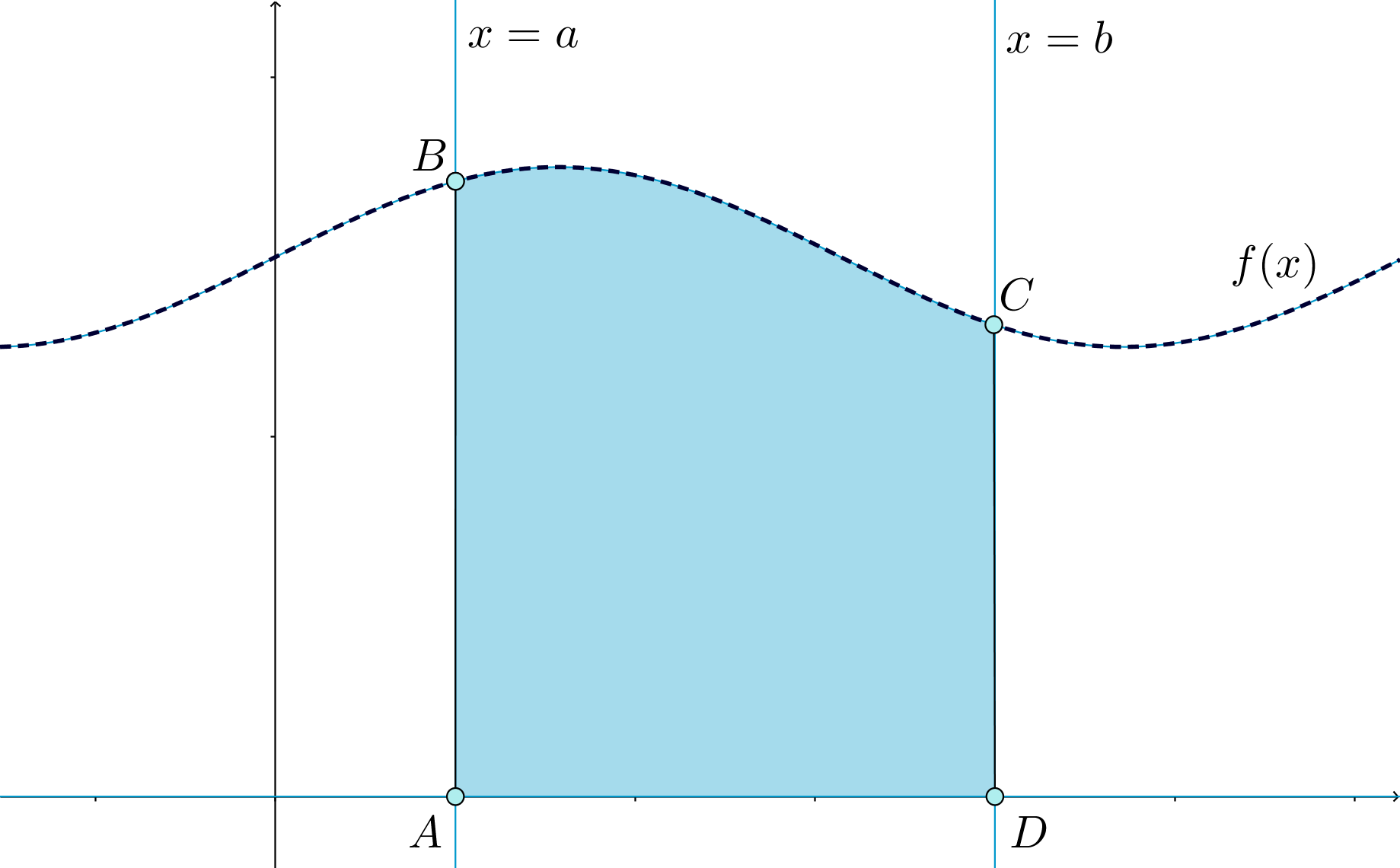
Формула Ньютона-Лейбница:
Тогда
равно площади закрашенной фигуры
,
называемой криволинейной трапецией: