Графики функций
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#540
Факт 1. Линейная функция – функция вида
, где
– некоторые
числа.
Графиком линейной функции является прямая.
Если
, то прямая проходит через начало координат.
Графиком
является прямая, параллельная оси
.
Графиком
является прямая, параллельная оси
.
Для
коэффициент
равен тангенсу угла наклона прямой к
положительному направлению оси
.
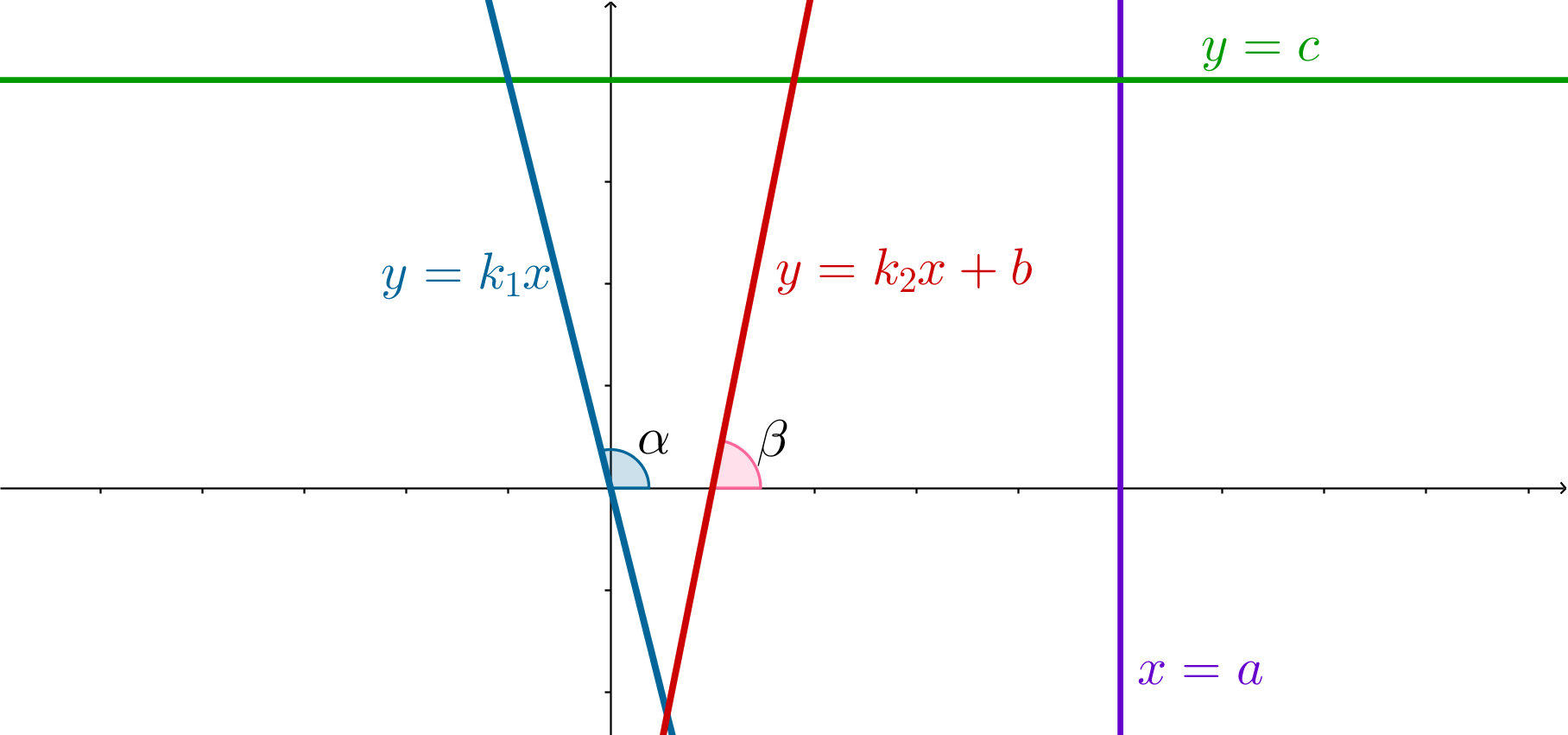
,
.
Если две прямые
и
параллельны, то
.
Если эти прямые взаимно перпендикулярны, то
.
Факт 2. Квадратичная функция – функция вида
, где
–
некоторые числа, причем
.
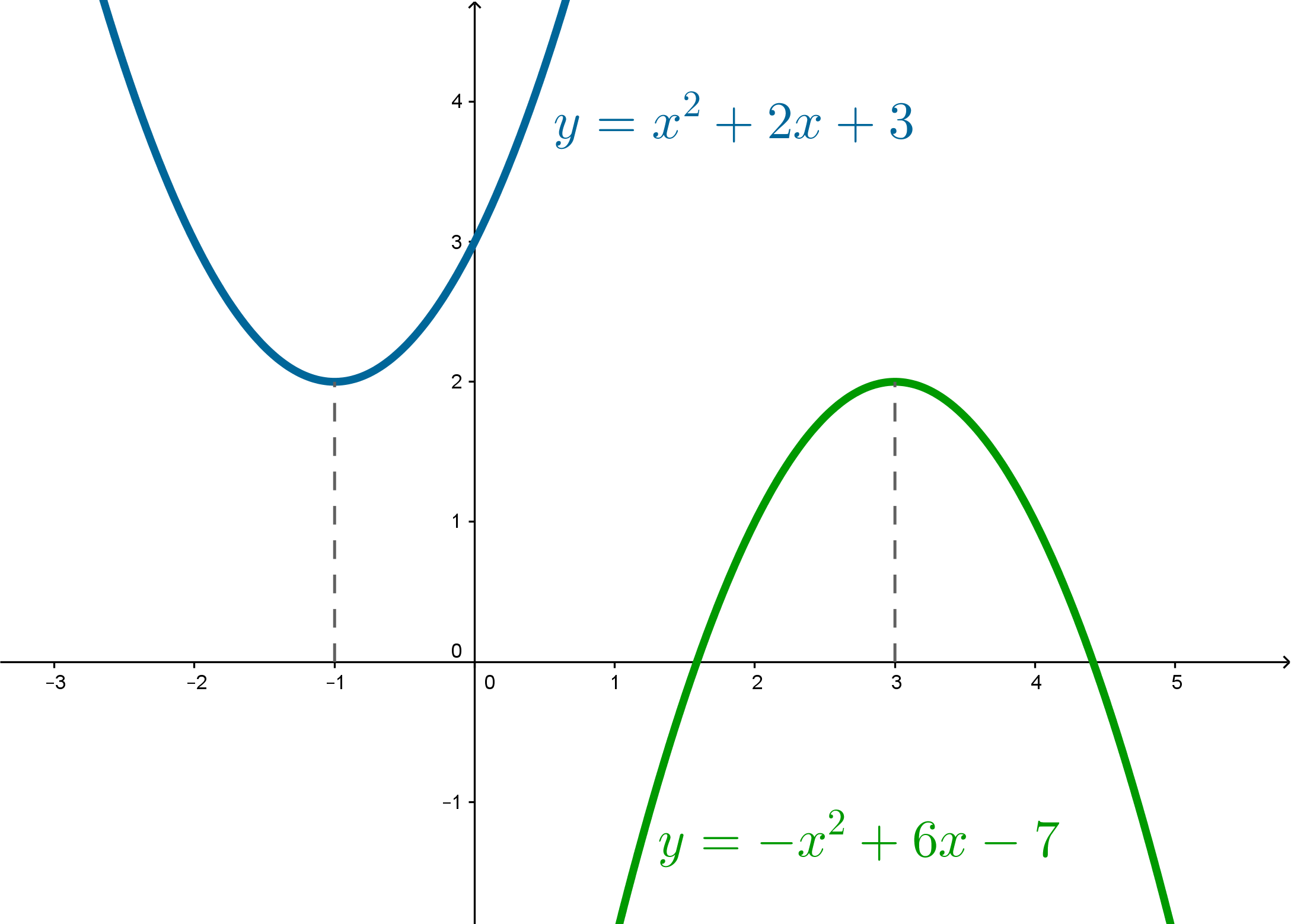
Графиком квадратичной функции является парабола.
Если
, то ветви параболы направлены вверх, если
– ветви
направлены вниз.
Абсцисса вершины параболы
Всякая парабола симметрична относительно прямой
.
Корни уравнения
– точки пересечения параболы с осью
.
Факт 3. Кубическая функция – функция вида
, где
–
некоторые числа, причем
.
Графиком кубической функции является кубическая парабола.
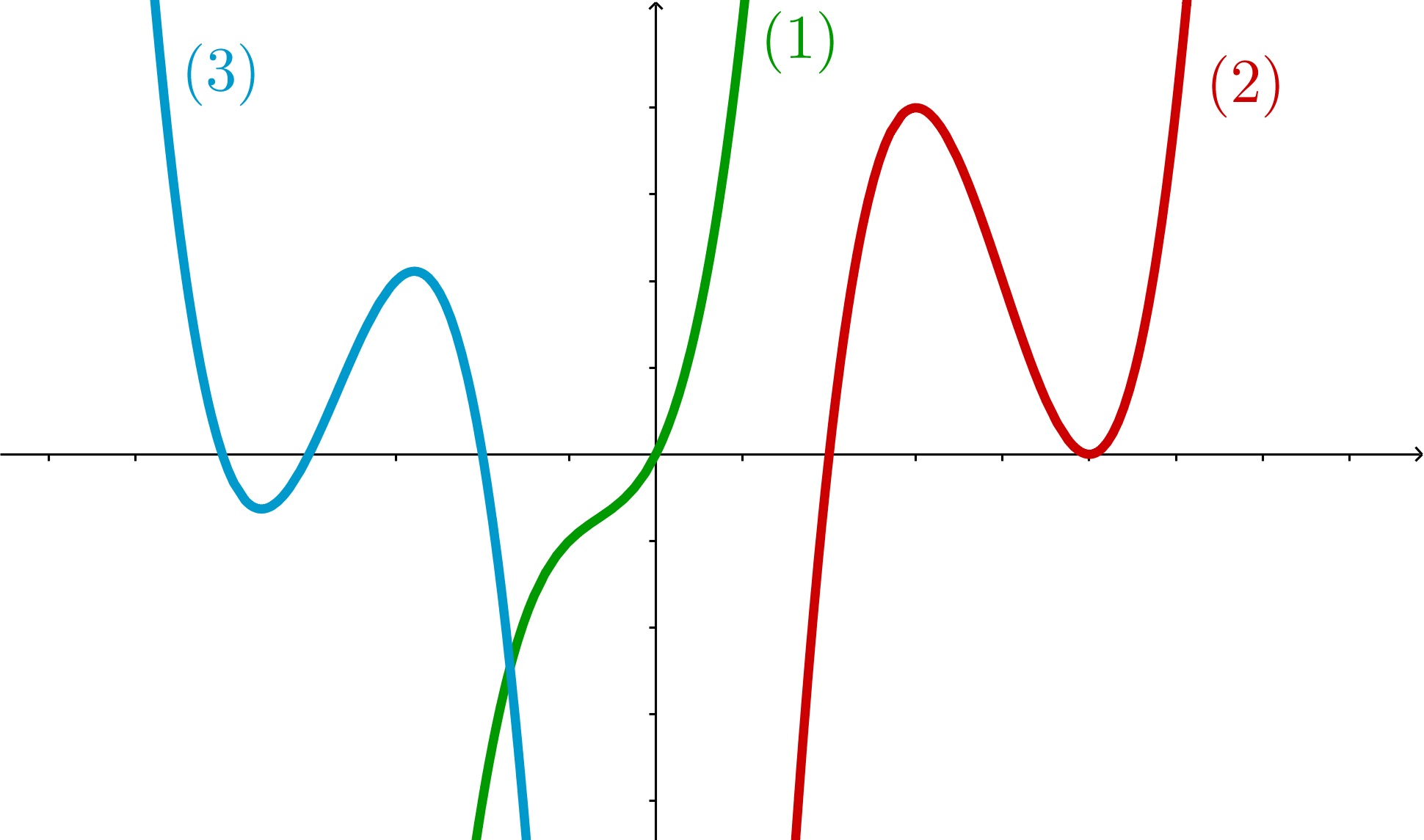
Если уравнение
имеет 1 корень, то график
выглядит, например, как
.
Если уравнение
имеет 2 корня, то график
выглядит, например, как
.
Если уравнение
имеет 3 корня, то график
выглядит, например, как
.
Факт 4. Функция корня – функция
.
График функции
:
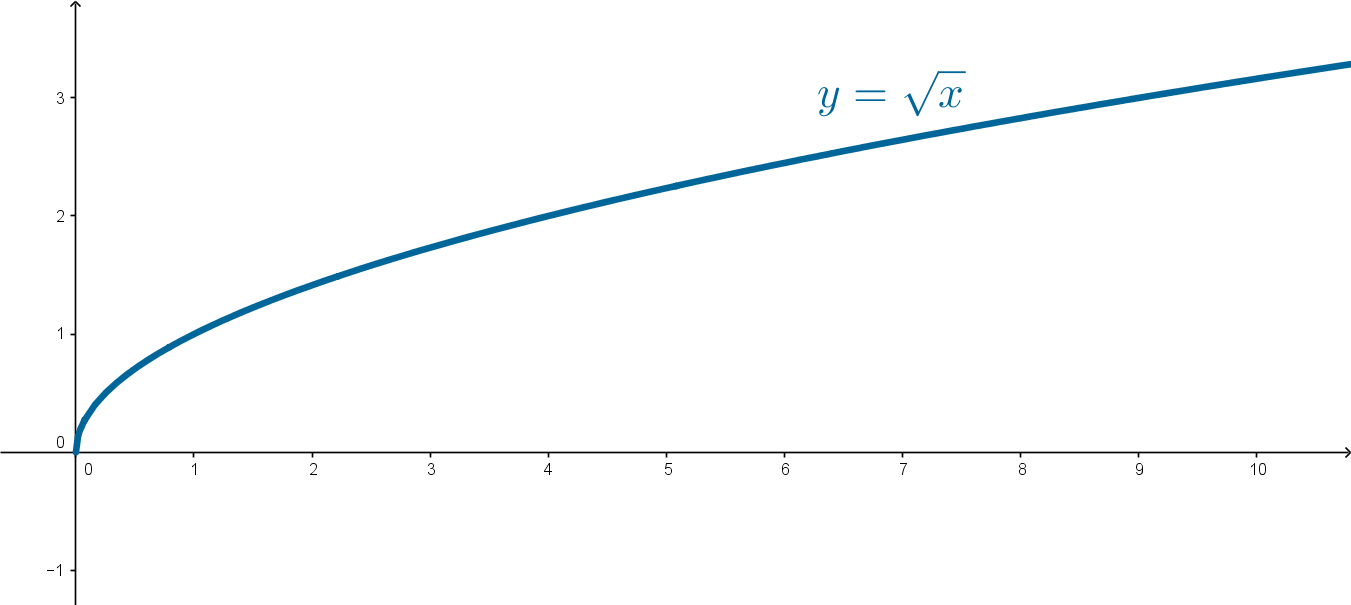
Заметим, что
определена при
и принимает значения
.
Факт 5. Графиком функции
является синусоида
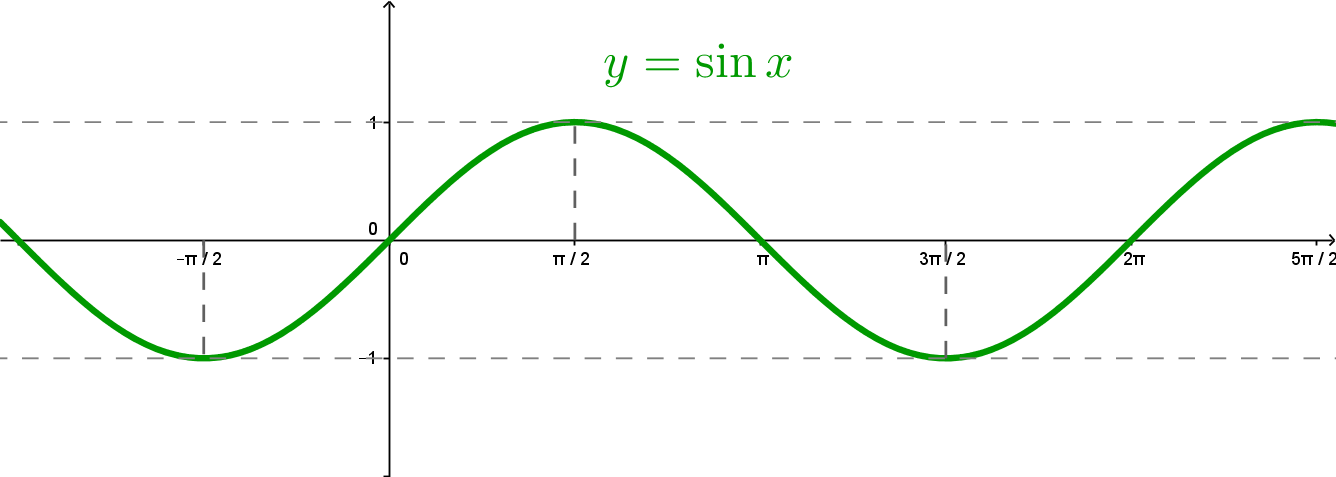
Графиком функции
также является синусоида, но сдвинутая на
единиц влево по оси
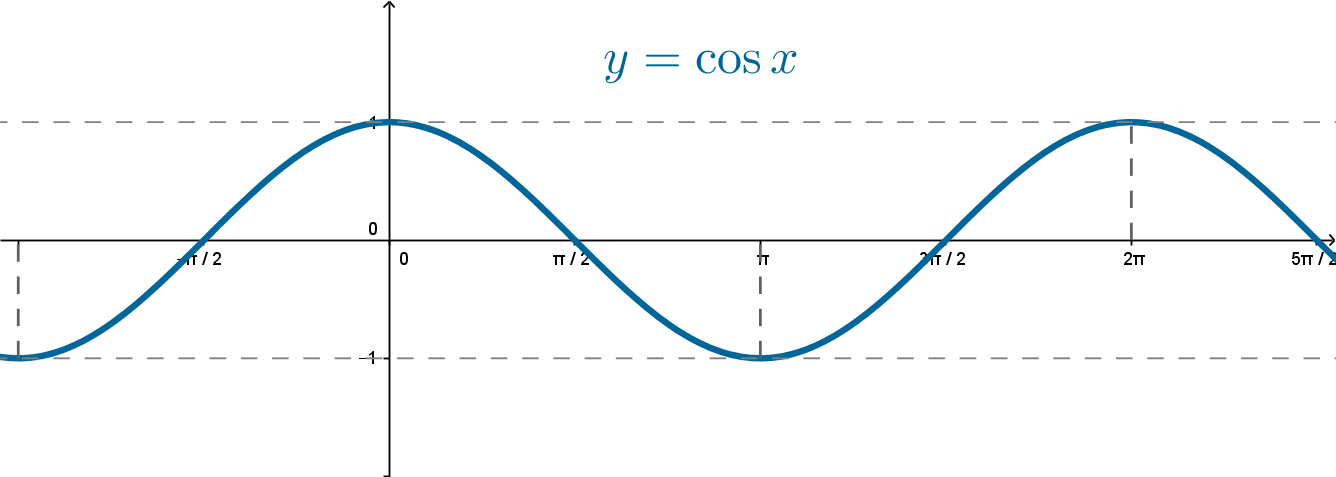
Обе функции
и
периодичны с периодом
. Обе
функции могут принимать значения
.
Функция
– нечетная, функция
– четная.
Факт 6. График функции
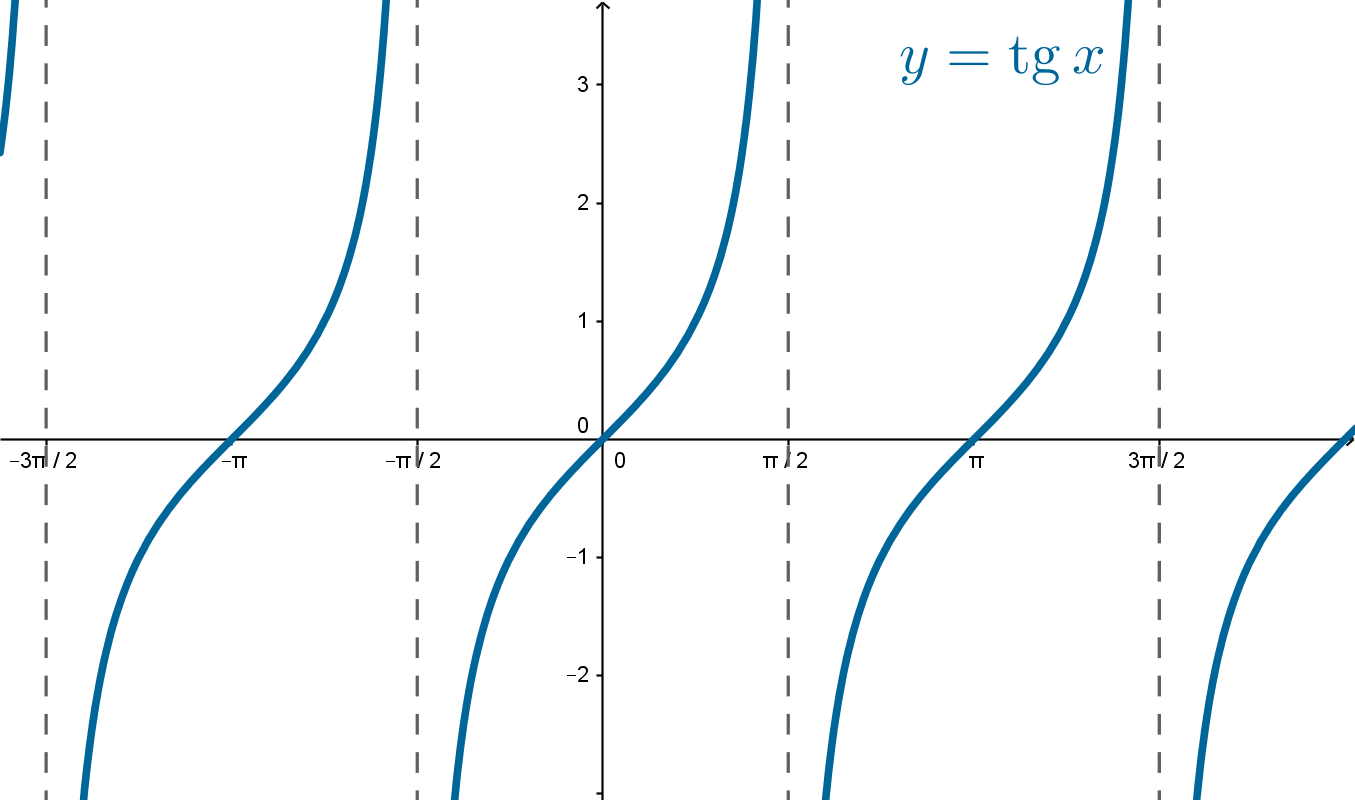
Прямые , где
– нечетное число, являются асимптотами графика
(то есть график их не пересекает).
График функции
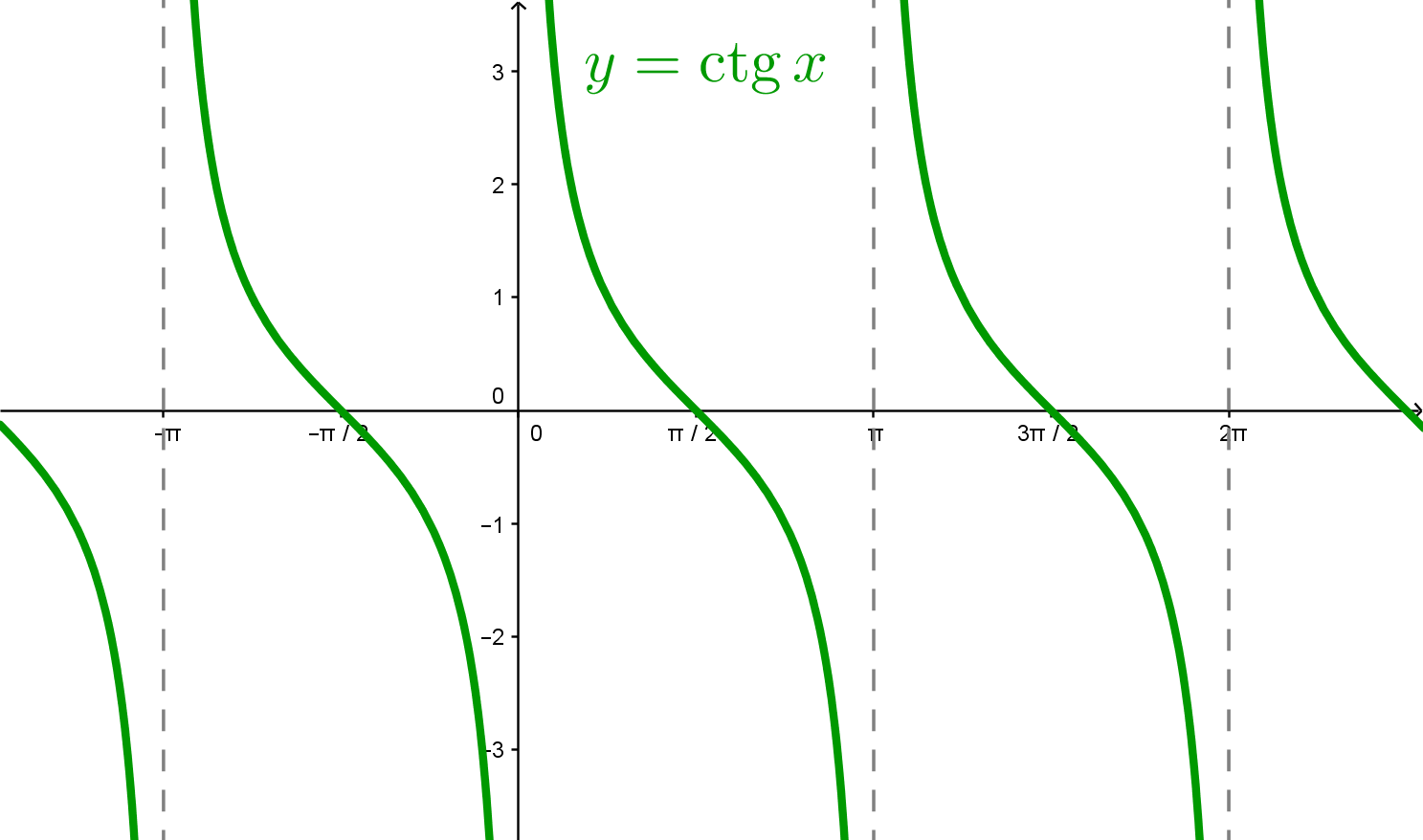
Прямые , где
– целое число, являются асимптотами графика (то
есть график их не пересекает).
Обе функции
и
периодичны с периодом
и нечетны.
Факт 7. Показательная функция
при
является возрастающей при
всех
, область значений
:
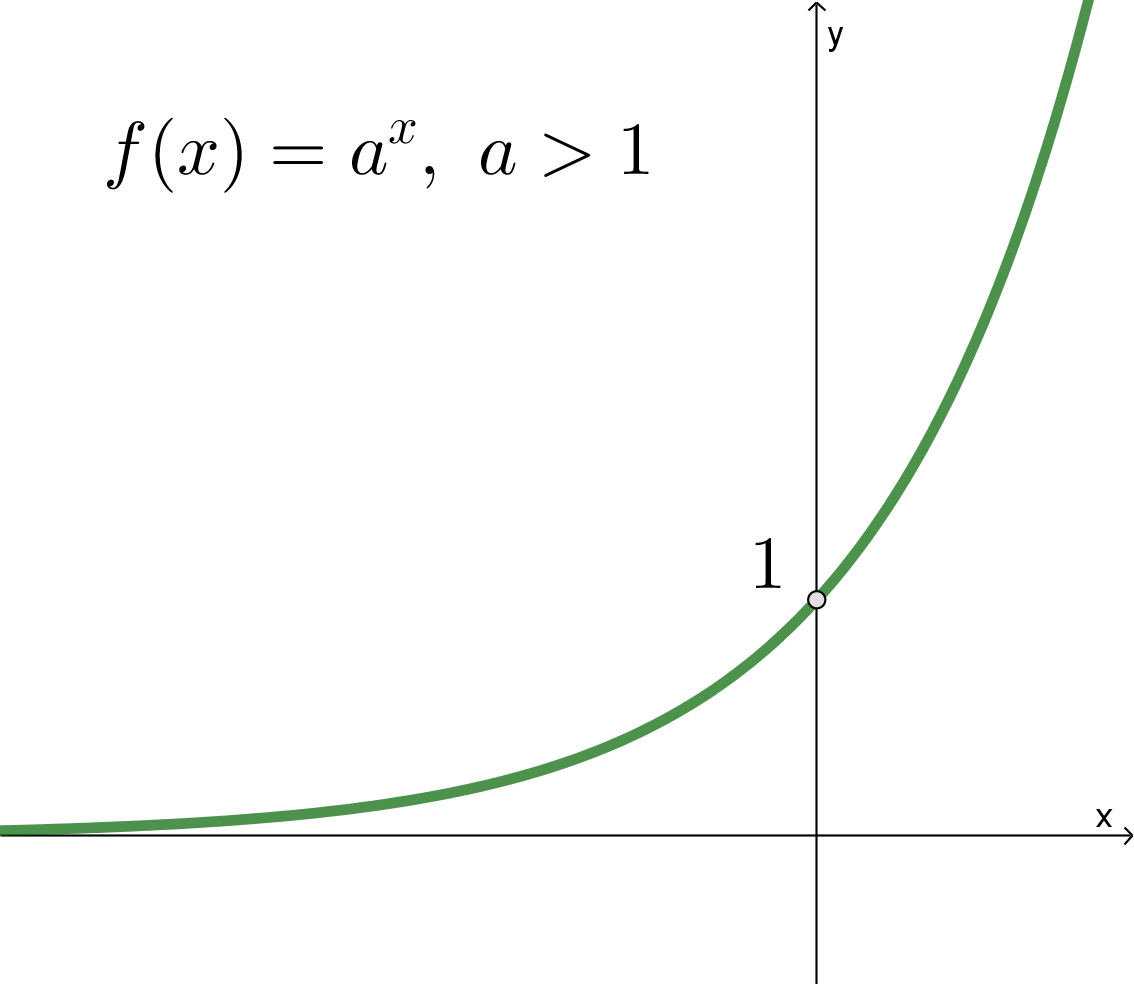
Ее график всегда проходит через точку .
Показательная функция
при
является убывающей при
всех
, область значений также
:
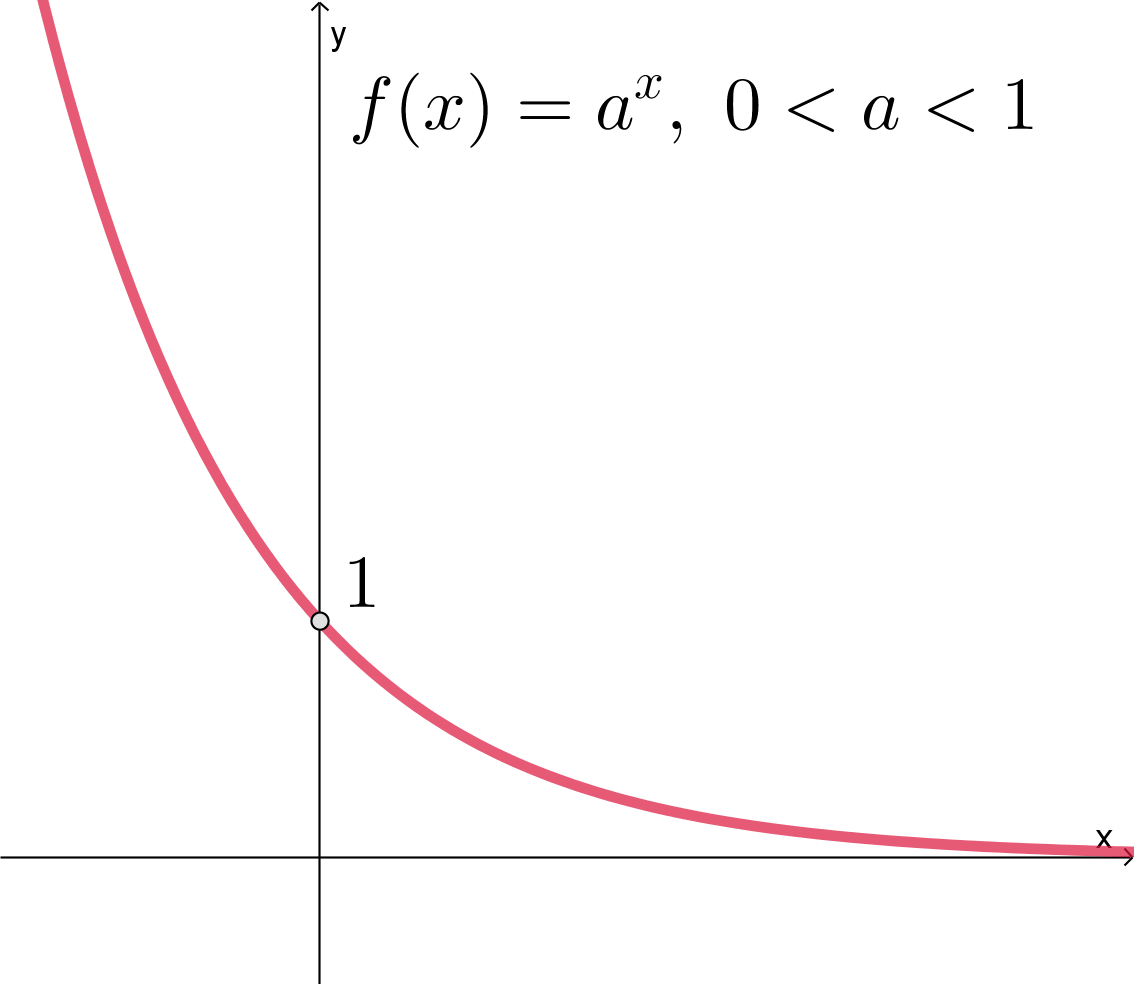
Ее график всегда проходит через точку .
Факт 8. Логарифмическая функция
при
является возрастающей, ее
область определения
, ее область значений
:

Ее график всегда проходит через точку .
Логарифмическая функция
при
является
убывающей, ее область определения
, ее область значений
:
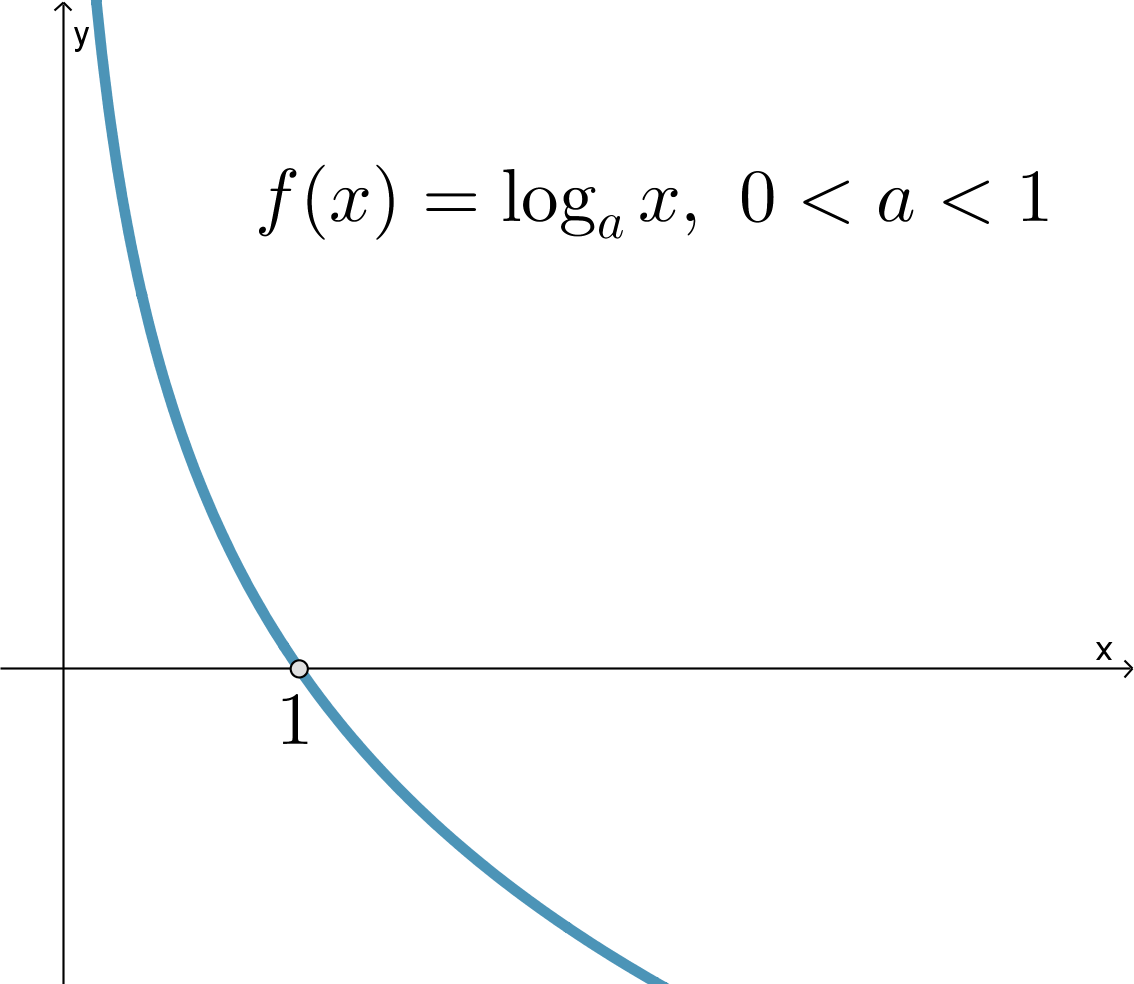
Ее график всегда проходит через точку .
