Показательные неравенства

$\blacktriangleright$ На ОДЗ верны следующие формулы:

$$\large{\begin{array}{|ll|} \hline a^0=1 &a^1=a\\ a^{nm}=(a^n)^m &a^n\cdot a^m=a^{n+m}\\ \dfrac{a^n}{a^m}=a^{n-m}&a^{-n}=\dfrac{1}{a^n}\\ a^n\cdot b^n=(a\cdot b)^n &\\ a^{\frac{k}{r}}=\sqrt[r]{a^k} \qquad \qquad \qquad \qquad& \dfrac{a^n}{b^n}=\left(\dfrac{a}{b}\right)^n\\&\\ a,b>0, \ \ a,b\ne 1, \ k\in \mathbb{Z},& r\in\mathbb{N}, \ m,n\in\mathbb{R}\\ \hline \end{array}}$$

 

$\blacktriangleright$ Стандартное показательное неравенство: $${\Large{a^{h(x)}\geqslant a^{g(x)} \ (*)}}$$ где $a>0,\ a\ne 1$
(на месте знака $\geqslant$ может стоять любой из знаков $\leqslant,\ >,\ <$)

 

Показательная функция $f(x)=a^x$ является возрастающей, если число $a>1$, и убывающей, если $0<a<1$, и определена при всех $x$ (то есть ее область определения $x\in\mathbb{R}$).

 

На графике приведен пример возрастающей показательной функции $f_1(x)=2^x$ и убывающей показательной функции $f_2(x)=(0,5)^x$.

 

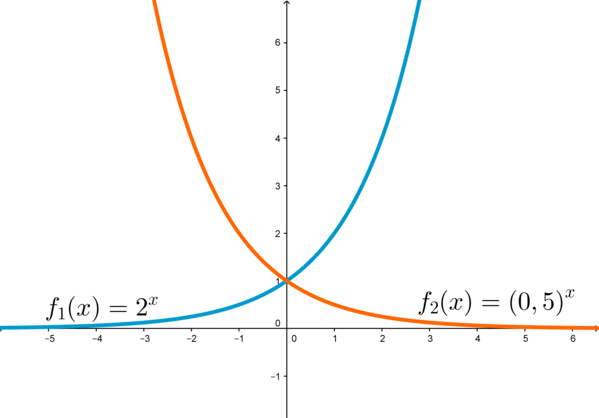
Напомним, что функция возрастает, если при увеличении $x$ увеличивается и $f(x)$. Функция убывает, если при увеличении $x$ уменьшается $f(x)$.

 

Действительно, для функции $f_1(x)=2^x$, например, $f_1(2)>f_1(3) \Leftrightarrow 4>8$, а для функции $f_2(x)=0,5^x$, например, $f_2(2)<f_2(3) \Leftrightarrow 0,25<0,125$.

 

Таким образом, неравенство $(*)$ есть не что иное, как сравнение $f(h)$ и $f(g)$. Если функция $f$ — возрастает, то неравенство $f(h)\geqslant f(g)$ равносильно неравенству $h\geqslant g$, а если убывает — то неравенству $h\leqslant g$.

 

Поэтому для того, чтобы решить неравенство $(*)$, нужно сравнить основание $a$ с единицей:

 

если ${\large{a>1}}$, то данное неравенство равносильно $${\Large{h(x)\geqslant g(x)}}$$

если ${\large{0<a<1}}$, то данное неравенство равносильно $${\Large{h(x)\leqslant g(x)}}$$

 

$\blacktriangleright$ Напомним, что область значений показательной функции — все положительные числа, т.е. $a^x>0$ при всех возможных $a$ и $x$.

 

$\blacktriangleright$ С помощью формулы ${\Large{b=a^{\log_ab}}}$ можно любое число $b>0$ представить в виде степени необходимого нам числа $a>0,\ a\ne 1$.

 

Пример 1. Решить неравенство $2^x>3^{x-1}$.

 

Нужно представить левую и правую части неравенства как степени с одинаковым основанием. Воспользовавшись формулой, можно записать $3=2^{\log_23}$. Тогда неравенство примет вид:

$2^x>2^{\log_23\cdot (x-1)}$. Т.к. основания $2>1$, то знак неравенства не будет меняться и данное неравенство равносильно неравенству

$x>\log_23\cdot (x-1)$. Отсюда $(1-\log_23)x>-\log_23$. Т.к. $\log_23>1$, то $(1-\log_23)<0$, значит, при делении правой и левой частей неравенства на $(1-\log_23)$ нужно изменить знак неравенства на противоположный, то есть $$x<-\dfrac{\log_23}{1-\log_23} \Leftrightarrow x<\dfrac{\log_23}{\log_23-1}$$ .

 

$\blacktriangleright$ Рассмотрим неравенства вида $${\Large{(f(x))^{h(x)}\lor(f(x))^{g(x)}}}$$ то есть когда в основании находится не конкретное число, а функция, также зависящая от $x$.

 

В таких неравенствах $f(x)$ может быть равно единице, если знак неравенства нестрогий (т.е. $\geqslant, \ \leqslant$) и если это не противоречит ОДЗ неравенства. Действительно, тогда мы получаем, например, $1^{h(x)}\geqslant 1^{g(x)}$, что верно, т.к. единица в любой степени дает единицу.

 

Таким образом, имеем: $$\textbf{I. }{\Large{(f(x))^{h(x)}> (f(x))^{g(x)} \quad \Leftrightarrow\quad \left[\begin{gathered} \begin{aligned} &\begin{cases} f(x)>1\\ h(x)> g(x) \end{cases}\\[2pt] &\begin{cases} 0<f(x)<1\\ h(x)< g(x) \end{cases} \end{aligned} \end{gathered} \right.}}$$

 

$$\textbf{II. }{\Large{(f(x))^{h(x)}\geqslant (f(x))^{g(x)} \quad\Leftrightarrow\quad \left[\begin{gathered} \begin{aligned} &\begin{cases} f(x)>1\\ h(x)\geqslant g(x) \end{cases}\\[2pt] &\begin{cases} 0<f(x)<1\\ h(x)\leqslant g(x) \end{cases}\\[2pt] &f(x)=1 \end{aligned} \end{gathered} \right.}}$$

 

Пример 2. Решить неравенство $x^{\sqrt{x-0,5}}\geqslant x^2$

 

Запишем ОДЗ: выражение под корнем должно быть неотрицательным, т.е. $x-0,5\geqslant 0 \Leftrightarrow x\geqslant 0,5$. Тогда на ОДЗ данное неравенство равносильно:

 

$\left[\begin{gathered} \begin{aligned} &\begin{cases} x>1\\ \sqrt{x-0,5}\geqslant 2 \end{cases}\\[2pt] &\begin{cases} 0<x<1\\ \sqrt{x-0,5}\leqslant 2 \end{cases}\\[2pt] &x=1 \end{aligned} \end{gathered} \right. \Rightarrow \left[\begin{gathered} \begin{aligned} &\begin{cases} x>1\\ x\geqslant 4,5 \end{cases}\\[2pt] &\begin{cases} 0<x<1\\ x\leqslant 4,5 \end{cases}\\[2pt] &x=1 \end{aligned} \end{gathered} \right. \Rightarrow x\in (0;1]\cup [4,5;+\infty)$

 

Пересекая полученный ответ с ОДЗ, получим $$x\in [0,5;1]\cup [4,5;+\infty)$$