Логарифмические неравенства

$\blacktriangleright$ На ОДЗ верны следующие формулы:

$$\large{\begin{array}{|lcl|} \hline \log_a1=0& \qquad & \log_aa=1\\ &&\\ \log_{a^n}{b^m}=\frac mn\log_{|a|}{|b|}&& a^{\log_bc}=c^{\log_ba}\\ &&\\ \log_a{bc}=\log_a{|b|}+\log_a{|c|}&& \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\\ &&\\ \log_ab\cdot \log_bc=\log_ac & \Longleftrightarrow & \log_bc=\dfrac{\log_ac}{\log_ab}\\ &&\\ \log_ab\cdot \log_ba=1 & \Longleftrightarrow & \log_ab=\dfrac1{\log_ba}\\ &&\\ \hline \end{array}}$$

$\blacktriangleright$ Стандартное логарифмическое неравенство $${\Large{\log_a{h(x)}\geqslant \log_a{g(x)} \quad (*)}}$$ где $a>0,\ a\ne 1$
(на месте знака $\geqslant$ может стоять любой из знаков $\leqslant,\ >,\ <$)

 

Логарифмическая функция $f(x)=\log_ax$ является возрастающей, если число $a>1$, и убывающей, если $0<a<1$, и определена при всех положительных $x$ (то есть ее область определения $x\in (0;+\infty)$).

 

На графике приведен пример возрастающей логарифмической функции $f_1(x)=\log_2x$ и убывающей логарифмической функции $f_2(x)=\log_{\,0,5}x$.

 

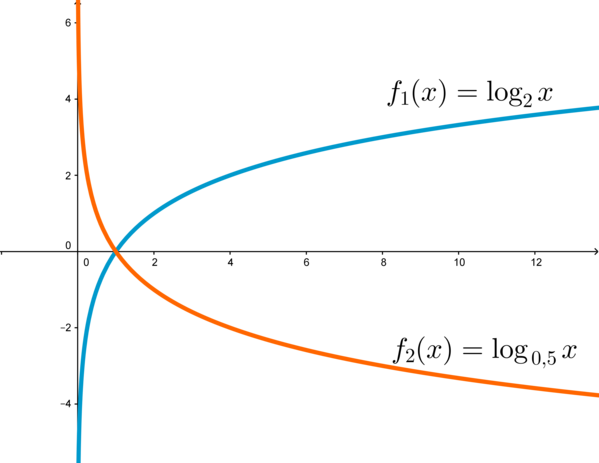
Напомним, что функция возрастает, если при увеличении $x$ увеличивается и $f(x)$. Функция убывает, если при увеличении $x$ уменьшается $f(x)$.

 

Таким образом, неравенство $(*)$ есть не что иное, как сравнение $f(h)$ и $f(g)$. Если функция $f$ — возрастает, то неравенство $f(h)\geqslant f(g)$ равносильно неравенству $h\geqslant g$, а если убывает — то неравенству $h\leqslant g$.

 

Поэтому для того, чтобы решить неравенство $(*)$, нужно сравнить основание $a$ с единицей:

 

если ${\large{a>1}}$, то данное неравенство равносильно системе (не забываем про ОДЗ!) $${\Large{\begin{cases} h(x)\geqslant g(x)\\ g(x)>0 \end{cases}}}$$ Заметим, что условие $h(x)>0$ учитывается автоматически в такой системе, т.к. если $h\geqslant g$, а $g>0$, то и $h>0$.

 

если ${\large{0<a<1}}$, то данное неравенство равносильно системе $${\Large{\begin{cases} h(x)\leqslant g(x)\\ h(x)>0 \end{cases}}}$$
Заметим, что условие $g(x)>0$ учитывается автоматически в такой системе.

 

$\blacktriangleright$ Напомним, что область значений логарифмической функции — все числа, т.е. $\log_ax\in \mathbb{R}$ при всех возможных $a$ и $x$.

 

$\blacktriangleright$ С помощью формулы ${\Large {b=\log_a{a^b}}}$ можно любое число $b$ представить в виде логарифма по необходимому основанию $a>0,\ a\ne 1$.

 

Пример 1. Решить неравенство $\log_2 {(x^2+7)}>4$

 

Представим по формуле $4=\log_2{2^4}=\log_2{16}$, тогда неравенство примет вид $$\log_2{(x^2+7)}>\log_2 {16} \Leftrightarrow \begin{cases} x^2+7>16\\ x^2+7>0 \end{cases}$$ (знак неравенства не сменится, т.к. основание логарифмов $2>1$).

Второе неравенство $x^2+7>0$ (это и есть ОДЗ) выполнено при всех $x$.
Первое неравенство системы равносильно $x^2-9>0 \Leftrightarrow (x-3)(x+3)>0 \Rightarrow x\in (-\infty;-3)\cup(3;+\infty)$.

 

Таким образом, после пересечения решений обоих неравенств системы решением исходного неравенства будут $x\in (-\infty;-3)\cup(3;+\infty)$.

 

$\blacktriangleright$ Рассмотрим неравенства вида $${\Large{\log_{h(x)}{f(x)}\geqslant \log_{h(x)}{g(x)}}}$$ (на месте знака $\geqslant$ может стоять любой из знаков $\leqslant,\ >,\ <$)
То есть когда в основании логарифма находится не конкретное число, а функция, зависящая от $x$.

 

Данное неравенство равносильно совокупности: $${\Large{\left[\begin{gathered} \begin{aligned} &\begin{cases} h(x)>1\\ f(x)\geqslant g(x)\\ g(x)>0 \end{cases}\\[4pt] &\begin{cases} 0<h(x)<1\\ f(x)\leqslant g(x)\\ f(x)>0 \end{cases} \end{aligned} \end{gathered} \right.}}$$

Иногда удобно выписать ОДЗ отдельно. Тогда неравенство будет равносильно системе: $${\Large{\begin{cases} f(x)>0 \quad (\textbf{ОДЗ})\\ g(x)>0 \quad (\textbf{ОДЗ})\\[3pt] \left[\begin{gathered} \begin{aligned} &\begin{cases} h(x)>1\\ f(x)\geqslant g(x) \end{cases}\\[3pt] &\begin{cases} 0<h(x)<1\\ f(x)\leqslant g(x) \end{cases} \end{aligned} \end{gathered} \right. \end{cases}}}$$

Пример 2. Решить неравенство $\log_x{(3x-1)}>1$

 

Данное неравенство равносильно:

$\log_x{(3x-1)}>\log_xx \ \Leftrightarrow \ \left[ \begin{gathered} \begin{aligned} &\begin{cases} x>1\\ 3x-1> x\\ x>0 \end{cases}\\ &\begin{cases} 0<x<1\\ 3x-1< x\\ 3x-1>0 \end{cases} \end{aligned} \end{gathered} \right. \ \Leftrightarrow \ \left[ \begin{gathered} \begin{aligned} &x>1\\ &\dfrac13<x<\dfrac12 \end{aligned} \end{gathered} \right. \ \Leftrightarrow \quad x\in \left(\dfrac13;\dfrac12\right)\cup\Big(1;+\infty\Big)$

 

Пример 3. Решить неравенство $\log_{x^2}{(x+1)^2}\leq 1$

 

Выпишем ОДЗ для аргумента логарифма: $(x+1)^2>0 \Rightarrow x\ne -1$.
Для основания логарифма ОДЗ отдельно выписывать не имеет смысла, т.к. мы будем учитывать его в самом решении: рассматривать случаи, когда основание больше $1$ и когда оно находится между $0$ и $1$.

 

Таким образом, на ОДЗ неравенство равносильно совокупности (учитывая, что $1=\log_{x^2}{x^2}$) $$\left[ \begin{gathered} \begin{aligned} &\begin{cases} x^2>1\\ (x+1)^2\leqslant x^2 \end{cases}\\[2pt] &\begin{cases} 0<x^2<1\\ (x+1)^2\geqslant x^2 \end{cases} \end{aligned} \end{gathered} \right. \quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} x^2-1>0\\ (x+1)^2-x^2\leqslant 0 \end{cases}\\[2pt] &\begin{cases} x^2<1\\ x^2>0\\ (x+1)^2- x^2\geqslant 0 \end{cases} \end{aligned} \end{gathered} \right.\quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} (x-1)(x+1)>0\\ (x+1-x)(x+1+x)\leqslant 0 \end{cases}\\[2pt] &\begin{cases} (x-1)(x+1)<0\\ x\ne 0\\ (x+1-x)(x+1+x)\geqslant 0 \end{cases} \end{aligned} \end{gathered} \right.\quad \Leftrightarrow \quad$$
$$\quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} x\in (-\infty;-1)\cup(1;+\infty)\\ x\in (-\infty;-\dfrac12\big] \end{cases}\\[2pt] &\begin{cases} x\in (-1;1)\\ x\ne 0\\ x\in\big[-\dfrac12;+\infty) \end{cases} \end{aligned} \end{gathered} \right. \quad \Leftrightarrow \quad x\in \Big(-\infty;-1\Big)\cup\Big[-\dfrac12;0\Big)\cup\Big(0;1\Big)$$

Пересекая данный ответ с ОДЗ ($x\ne -1$), получим тот же ответ.

 

$\blacktriangleright$ Таким образом, как правило, для того, чтобы система (совокупность) не выглядела слишком огромной, удобно записывать ОДЗ неравенства отдельно, а затем просто пересекать решение системы (совокупности) с этим ОДЗ. Что мы и сделали в примере $3$.