Механика

Баллистика. Бросок под углом к горизонту

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Механика

Теоретическая справка

#604

Основные формулы

Горизонтальный бросок

Время всего полета:

∘ --- tпол = 2H- g

Дальность полета:

∘ --- 2H- L = v0 g

Тангенс угла наклона траектории полета тела:

v gt tgα = yv-= v- x 0

Бросок под углом к горизонту

Время всего полета:

tпол = 2v0sin-α g

Время подъема (падения):

t v sinα tпод = tпад = по2л=-0-g--

Максимальная дальность полета:

Lmax = v20sin2α- g

Максимальная высота подъема:

2 2 Hmax = v0sin-α- 2g

Траектория движения:

g---x2-- y =tgαx − 2v20cos2 α

Понятие баллистики

Баллистика — наука о движении тел, брошенных в пространстве, основанная на математике и физике. При этом тела рассматриваются как материальные точки.

По сути, баллистика для нас сводится к тому, что уравнения движения брошенного тела проецируются на оси координат, введенные удобным для каждой задачи образом. То есть в баллистике мы в основном работаем с проекциями векторов, разбивая движение точки на две составляющие — движение по горизонтальной и вертикальной оси.

Горизонтальный бросок

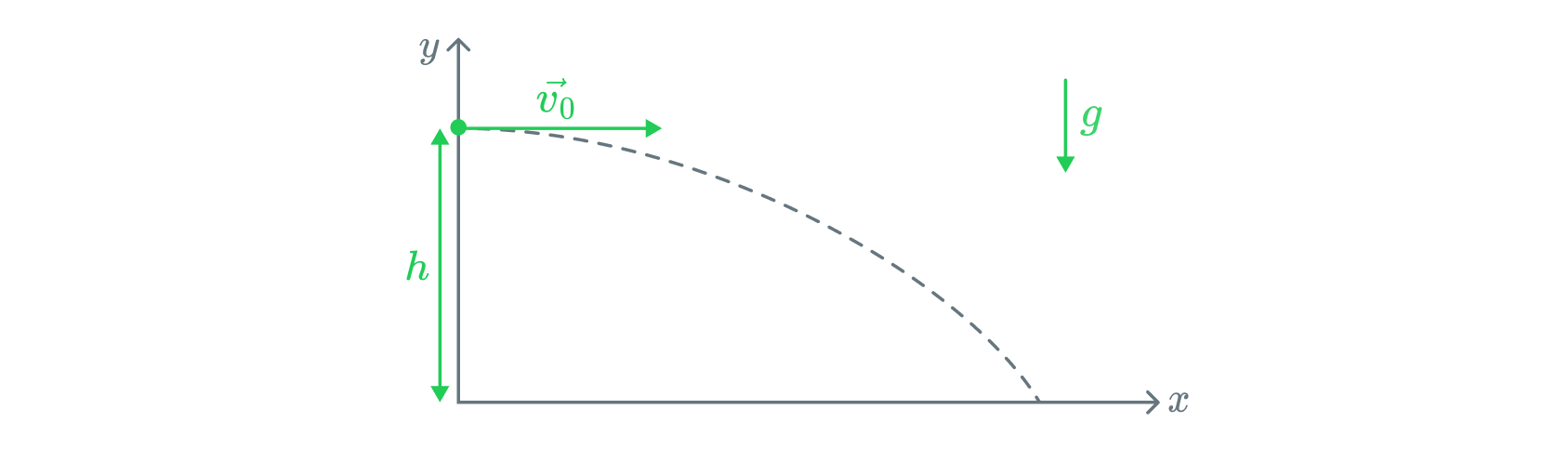
Рассмотрим ситуацию, когда тело брошено горизонтально с начальной скоростью $v0$ с некоторой высоты $h$ . Проведем качественный анализ всех зависимостей во время движения тела. Для этого введем систему координат как показано на рисунке:

$PIC$

Вспомним уравнение равноускоренного движения материальной точки:

⃗at2 ⃗r(t)= ⃗r0+ ⃗v0t+ 2--

Теперь спроецируем данное уравнение на координатные оси:

(| 2 ||{y = y0+ v0yt+ ayt- | 2 2 ||(x = x0+ v0xt+ axt- 2

Проанализируем полученные проекции. В данном случае координата $x0$ равна нулю, а координата $y0$ равна $h$ , с которой было брошено тело. Проекция вектора начальной скорости $⃗v0$ на ось $y$ нулевая (вектор при проецировании на ось $y$ обращается в точку), а на ось $x$ проекция равна модулю вектора $v0x = v0$ . На тело действует только ускорение свободного падения $⃗g$ , которое направлено вертикально вниз. Исходя из этого, проекция ускорения на ось $x$ нулевая, а на ось $y$ равна $ay =− g$ .

С учетом наших рассуждений запишем систему уравнений в виде:

(| 2 ||{ y(t)= h − gt- | 2 ||( x(t)= v0t

Обозначим дальность полета тела за $L$ . Тогда справедливы следующие соотношения:

( 2 |||{h = gt- 2 |||(L = v t 0

Мы разобрались с координатами, теперь разберемся со скоростями. Запишем уравнение для скорости при равноускоренном движении материальной точки в векторном виде:

⃗v(t)= ⃗v0+ ⃗at

Спроецируем данное уравнение на оси координат аналогично предыдущему:

( |||{ vy(t)= v0y + ayt |||( v (t)= v + a t x 0x x

Воспользуемся нашими рассуждениями о проекциях скорости и ускорения тела, тогда систему уравнений можно представить в виде:

( ||| {vy(t)= − gt ||| (vx(t)= v0

Таким образом, можно сделать вывод, что по оси $y$ тело движется равноускоренно, а по оси $x$ — равномерно.

Далее рассмотрим следующую задачу: пусть при известной начальной скорости $v0$ и начальной высоте $H$ мы хотим найти время полета — время движения тела с момента броска до момента приземления. Для этого необходимо лишь подставить в зависимость вертикальной координаты конечное положение тела. Так как тело будет находиться на земле, то $y$ =0, тогда получим:

∘ --- gt2 2H- y(t)= h− 2 = 0 ⇒ tпол = g

Получили примечательный результат: время полета не зависит от начальной скорости. При этом важно держать в голове, что в данном случае речь идет только про горизонтальный бросок. Вычислим также дальность такого броска, для этого необходимо вспомнить про аналогичную зависимость для горизонтальной координаты:

x(t)= v0t

Подставляя полученное выражение для длительности полета $tпол$ , получим выражение для дальности броска $L$ :

∘ --- x(t) =v0t= L ⇒ L = v0 2H- g

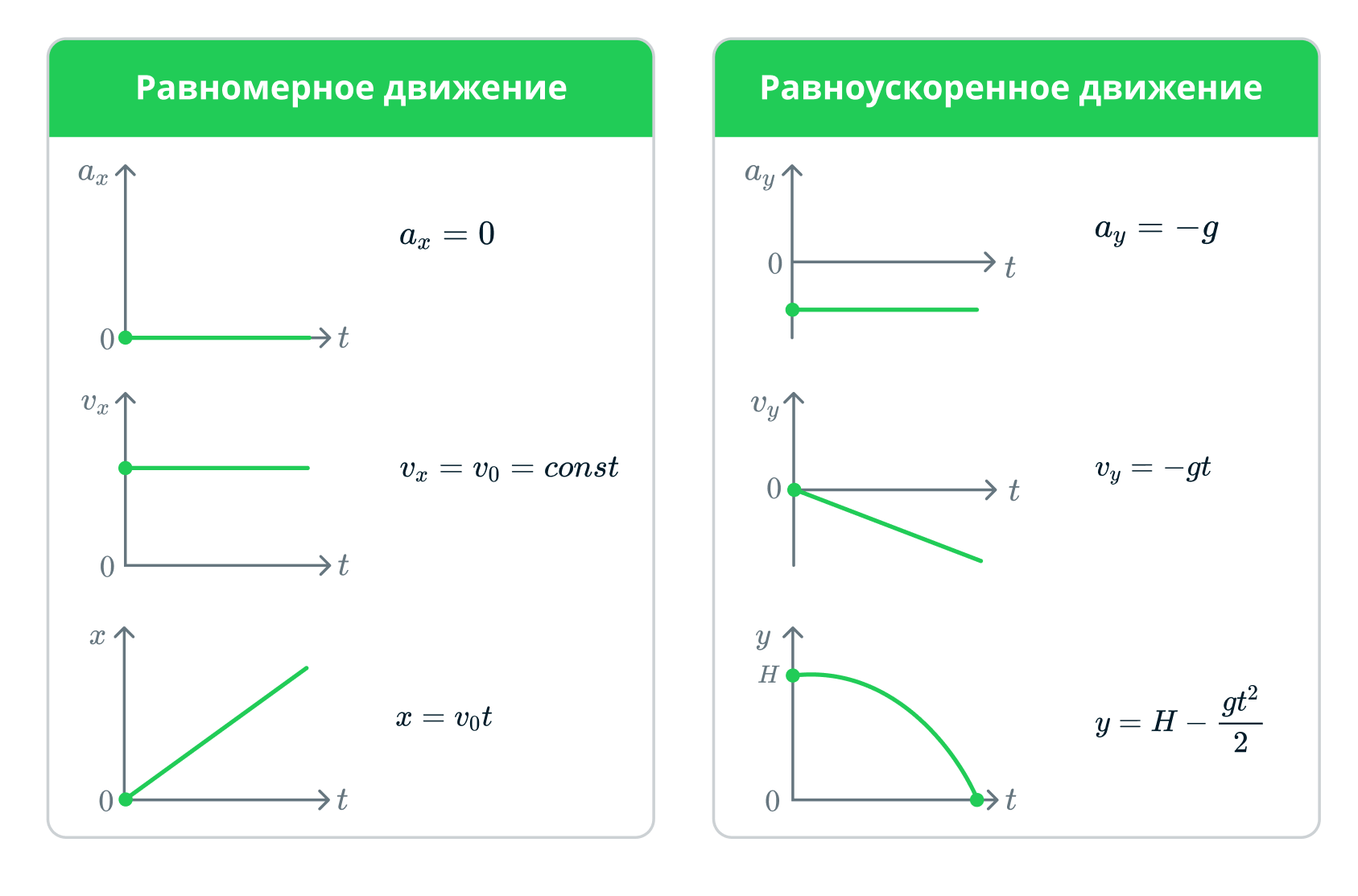
Изобразим графики всех зависимостей от времени:

$PIC$

Теперь посмотрим как меняется тангенс угла между вектором скорости тела и горизонтом. Для этого рассмотрим некоторую точку на траектории, в которой тело движется со скоростью $⃗v$ . Разобьем вектор $⃗v$ на проекции $vy$ и $vx$ , как показано на рисунке.

$PIC$

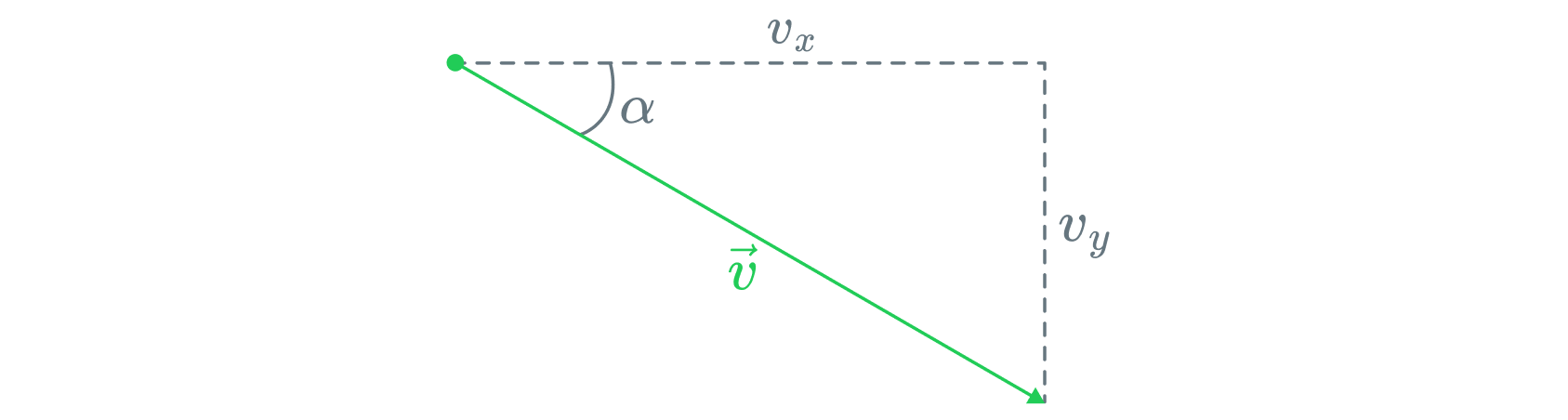
По теореме Пифагора можно выразить модуль скорости $v$ :

∘ --2---2- ∘-----2---2 v = vy + vx = (−gt) + v0

Обозначим интересующий нас угол за $α$ . Тогда используя определение тангенса, а также полученные выражения для проекций скорости, получим:

|vy| gt tgα = |vx| = v0-

Бросок под углом к горизонту

Теперь рассмотрим более сложную ситуацию: тело брошено под углом $α$ к горизонту с начальной скоростью $⃗v0$ . Чтобы рассматривать эту конструкцию, опять введем систему координат как показано на рисунке.

$PIC$

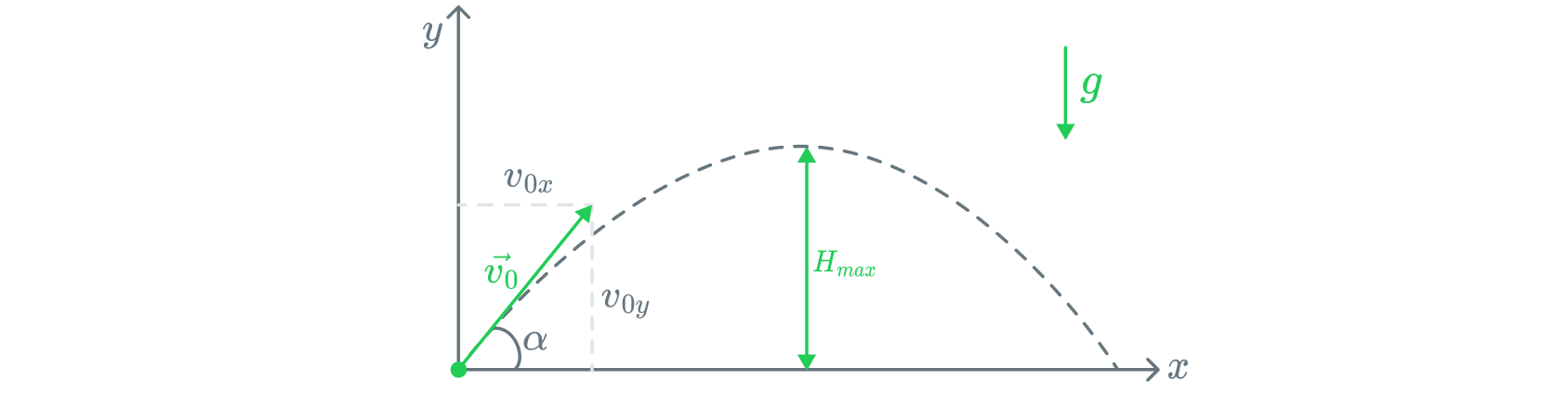
Аналогично предыдущему пункту, сначала разбираемся с зависимостями координат. Во-первых, мы ввели систему координат так, что точка броска находится в нуле, поэтому $y0 = x0 =0$ . Также заметим, что горизонтальное движение равномерное, а значит $a = 0 x$ . И наконец воспользуемся тем, что $ay =− g$ . Тогда уравнения преобразуются:

( ( || ayt2 || gt2 |{y = y0+ v0yt+ -2-- |{y = v0yt− -2- || a t2 ⇒ || |(x = x0+ v0xt+ -x2-- |(x = v0xt

Теперь разберемся со скоростями. С учетом того, что проекция вектора начальной скорости $⃗v0$ на ось $y$ равна $v0y = v0sinα$ , а на ось $x$ равна $v0x = v0cosα$ , запишем систему уравнений в виде:

( ( ||| ||| { vy = v0y + ayt ⇒ { vy = v0sinα − gt ||| ||| ( vx = v0x+ axt ( vx = v0cosα

Используя полученные уравнения, определим времена подъема и полета. Для этого поймем, что в верхней точке вертикальная проекция скорости $vy$ равна нулю. Тогда имеем:

vsinα vy = v0sinα − gt =0 ⇒ tпод = 0-g---

Теперь найдем время всего полета. Когда тело приземлится на землю, его координата по вертикальной оси будет равняться нулю. Воспользуемся этим:

gt2 ( gt) y = v0sinαt−-2- =0 ⇒ t v0sin α− 2- = 0

Произведение может быть равно нулю либо когда $t= 0$ , либо когда выражение в скобках равно нулю. Случай, когда $t= 0$ соответствует моменту, в который тело еще не совершило полет, а значит нам не подходит. Поэтому рассматривая второй случай, получим искомое выражение:

v0sin α− gt= 0 ⇒ tпол = 2v0sin-α 2 g

При этом движение тела при таком броске симметрично (этот факт мы докажем позднее), поэтому можно утверждать, что время подъема и время падения равны $tпол = tпад$ .

Теперь найдем выражения для максимальной высоты и дальности полета тела. Зная зависимость горизонтальной координаты от времени, подставим в нее время всего полета и получим дальность:

2v sin α v2sin2α x= v0xt ⇒ Lmax =v0cosα--0g--- ⇒ Lmax =-0-g---

Заметим, что длина полета будет максимальной в случае, если тело было брошено под углом 45 $∘$ к горизонту. В данном случае $sin2α$ максимален и равен 1.

Аналогично, подставляя время подъема в зависимость вертикальной координаты от времени, найдем максимальную высоту подъема:

gt2 v0sinα- g( v0sinα-)2 y = v0yt− 2 ⇒ Hmax = v0sinα g − 2 g

Тогда упрощая выражение получим следующее выражение:

Hmax = v20sin2α- 2g

Однако эту формулу можно получить и другими способами. Для вспомним выражение для перемещения, выраженное через начальные и конечные скорости:

Sy = vк2y-− v20y 2ay

где в точке с максимальной высотой $vкy = 0$ . Это объясняется тем, что иначе тело бы имело вертикальную проекцию скорости, а значит в следующий момент времени оно поднялось бы еще выше. При этом мы также знаем, что вертикальное перемещение $Sy$ в точности равно максимальной высоте полета: $Sy = Hmax$ . Вспоминая, что $ay =− g$ , имеем:

0−-v20y- −v0sin2α v02sin2α- Hmax = −2g ⇒ Hmax = − 2g ⇒ Hmax = 2g

И, наконец, рассмотрим третий способ получения этой формулы. Рассмотрим движение тела из положения с максимальной высотой до момента его падения на землю. Этот подход сводит нашу задачу к горизонтальному броску, который был разобран в предыдущей главе. Тогда пользуясь уже имеющимися знаниями запишем результат:

2 Hmax = gtпад 2

где время падения $tпад =v0sinα∕g$ . Подставляем и получаем формулу:

H = v20sin2α- max 2g

Обратим внимание, что готовых формул для $tпод$ , $tпад$ , $tпол$ , $Lmax$ и $Hmax$ нет в кодификаторе, поэтому для задач из второй части их вывод необходимо будет показать.

Теперь изобразим графики всех зависимостей от времени:

$PIC$

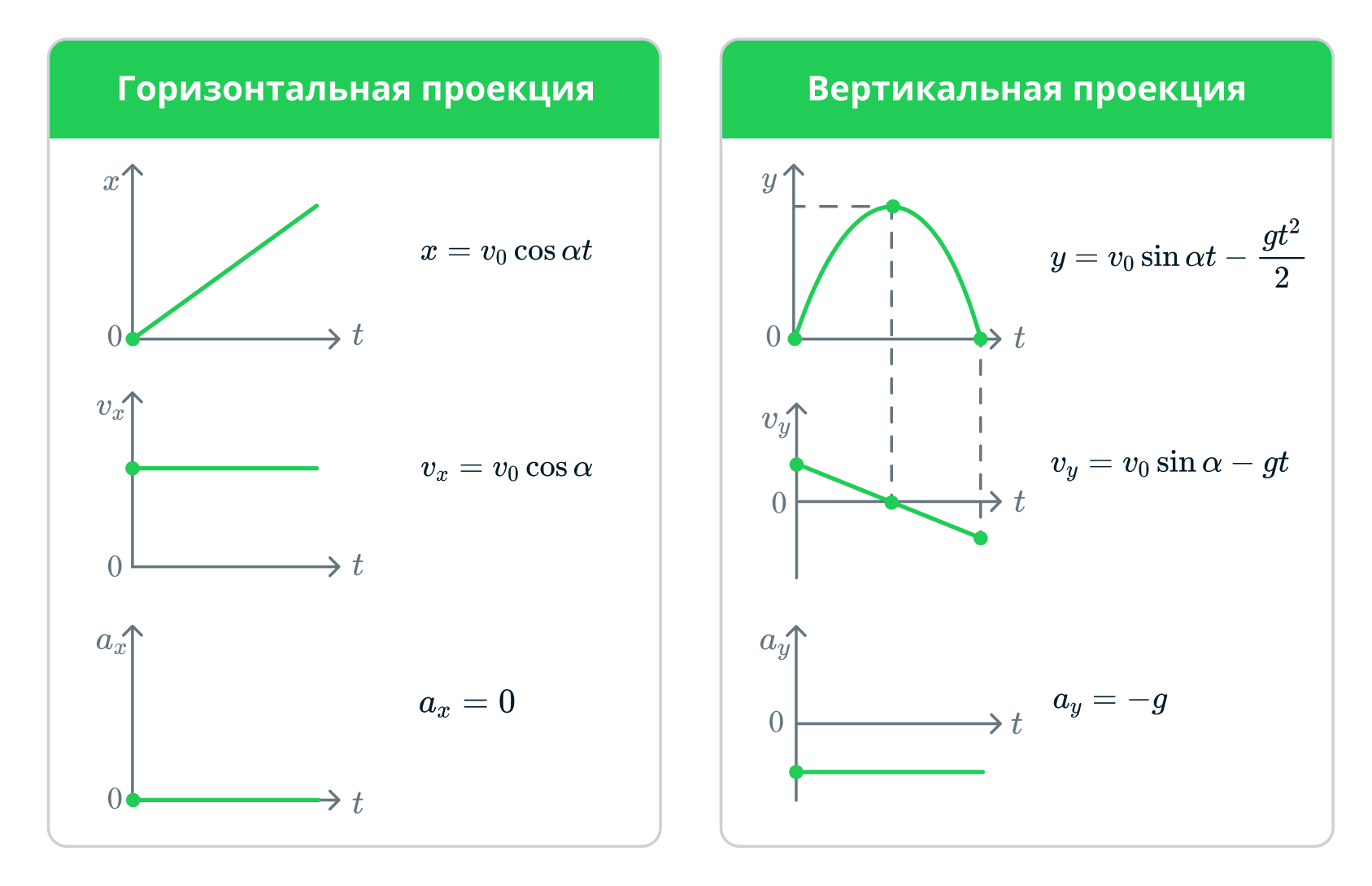
Далее найдем траекторию $y(x)$ движения тела, брошенного под углом к горизонту. Для этого запишем систему уравнений, определяющих положение тела в пространстве:

(| 2 ||{y = v0sinαt− gt- | 2 ||(x = v0cosαt

Выразим из второго уравнение время:

--x--- x = v0 cosαt ⇒ t= v0cosα

и подставим его в выражение для $y(t)$ :

x g x2 y = v0sin α⋅v-cosα − 2 ⋅v2cos2α 0 0

Немного преобразуем уравнение и получим зависимость $y(x)$ :

y(x)= tgα⋅x − g--x2--- 2v20cos2α

Заметим, что графиком данной функции является парабола. Мы знаем, что парабола симметрична относительно своей вершины, поэтому времена подъема $tпод$ и падения $tпад$ равны. Но так как время полета равно сумме времени подъема и падения, то имеем:

tпол = 2tпод = 2tпад

Предыдущая справка

Следующая справка