Механика

Движение по окружности

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Механика

Теоретическая справка

#605

Основные формулы

Угловая скорость:

ω = Δ-φ = v-= 2π =2πν Δt R T

Связь линейной и угловой скорости:

v =ωR

Период вращения при равномерном движении по окружности:

t 2πR 2π T = N-= -v--= ω-

Частота вращения:

N 1 ω ν =-t = T-= 2π

Центростремительное (нормальное) ускорение:

2 an = υ = ω2R R

Тангенциальное ускорение:

aτ = dv = v′(t) dt

Полное ускорение в векторном виде:

⃗aполн = ⃗aτ + ⃗an

Полное ускорение в скалярном виде:

aполн =∘a2n+-a2τ

Равномерное движение по окружности

Равномерное движение по окружности — частный случай криволинейного движения, когда вектор скорости тела не изменяется по модулю (длина вектора постоянна), а изменяет лишь свое направление. Таким образом, выполняется следующее соотношение:

|⃗v|= const

$PIC$

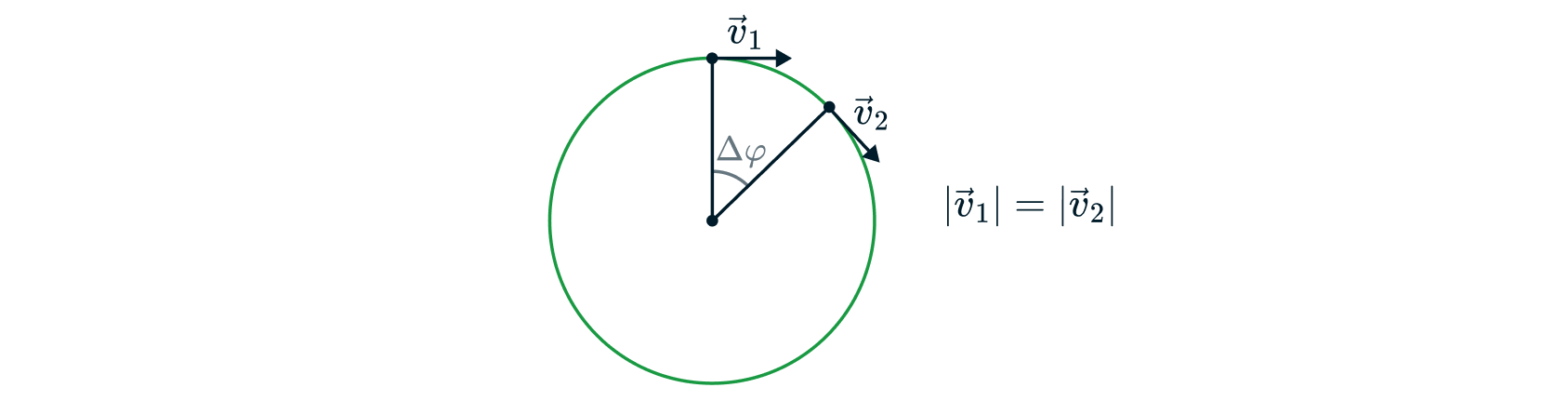
Угловая скорость при равномерном движении по окружности — это отношение угла поворота радиус вектора направленного за некоторый промежуток времени:

ω = Δ-φ Δt

При неравномерном движении по окружности угловая скорость вводится как производная угла поворота по времени:

dφ ′ ω = dt-=φ (t)

Единицы измерения: $[ω]=$ рад/c (радиан в секунду) $=$ $с−1$

Связь линейной и угловой скорости

Угол в радианной мере вводится как отношение длины дуги окружности к ее радиусу:

$PIC$

Δl- Δ φ= R

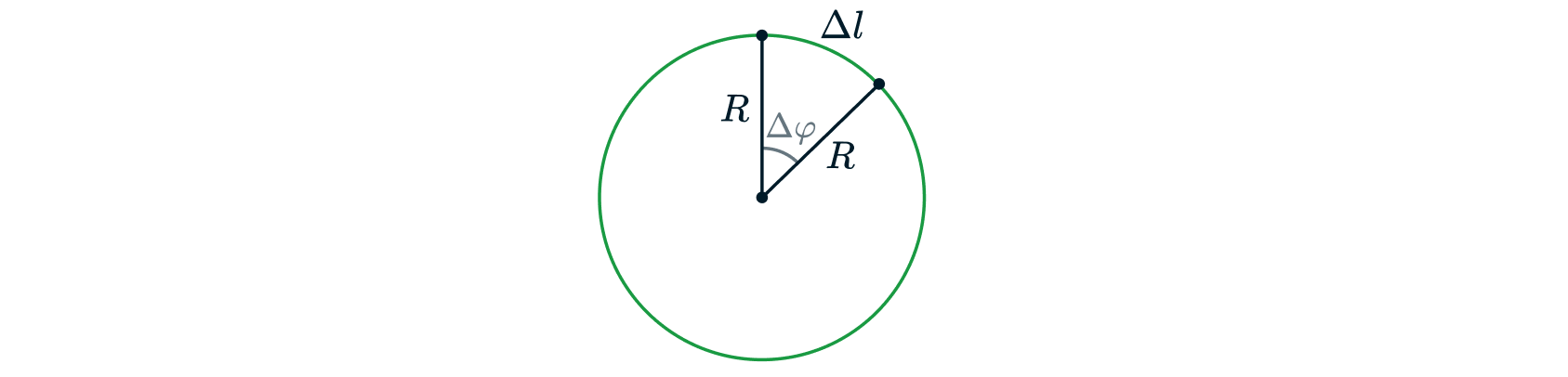
Поскольку движение равномерное, длину дуги можно выразить через линейную скорость и время движения:

Δl = RΔφ = vΔt

Выразим линейную скорость:

v = Δ-φR = ωR Δt

Откуда видна связь линейной и угловой скорости:

v =ωR

Период обращения — это время одного полного оборота. То есть для равномерного движения по окружности — это отношение времени обращения к числу оборотов:

-t T = N

Единицы измерения: $[T]=$ с (секунда).

При равномерном движении эта формула может принимать и другой вид. Пусть двигаясь со скоростью $v$ по окружности, тело совершает один оборот за $T$ секунд. Таким образом, оно проходит расстояние, равное длине окружности $2πR$ .

Обращая это выражение в формулу, получим:

v = 2πR- ⇒ T = 2πR-= 2π T v ω

Частота вращения — это величина, обратная периоду. Частота показывает, сколько полных оборотов совершается в единицу времени.

ν = N = ω- = 1- t 2π T

Единицы измерения: $[ν]=$ об/c (оборот в секунду) Гц (герц) $=$ $с−1$

Также свяжем угловую скорость с частотой и периодом:

ω = 2π = 2πν T

Центростремительное (нормальное) ускорение

При равномерном движении по окружности направление вектора скорости постоянно меняется. Это происходит из-за наличия центростремительного (нормального) ускорения, направленного перпендикулярно вектору скорости $⃗an ⊥ ⃗v$ в центр окружности. В дальнейшем будем называть его нормальным.

$PIC$

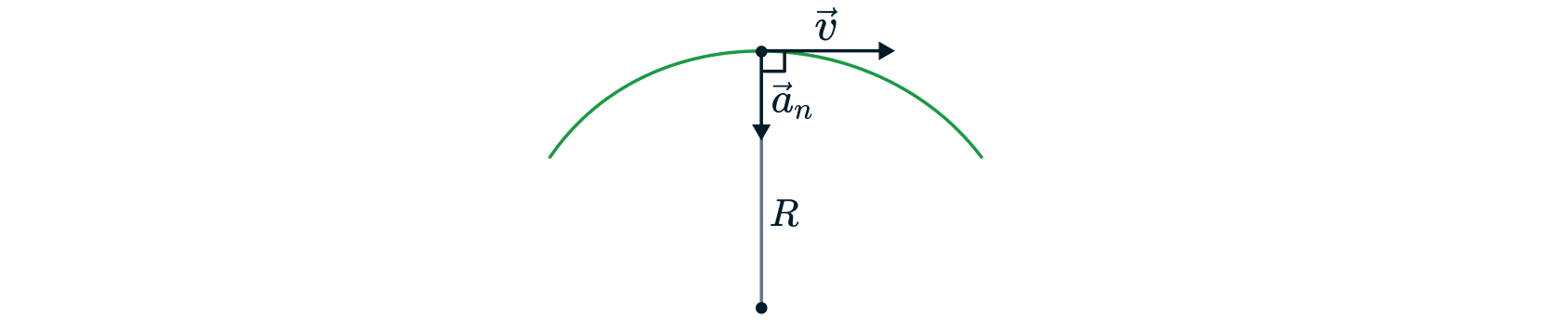
Нормальное ускорение вычисляется по формуле:

v2 an =-R = ω2R

Давайте ее выведем. Для этого рассмотрим тело, движущееся по окружности с постоянной угловой скоростью, в два момента времени. Проведем радиус-векторы $⃗R1$ и $⃗R2$ к положениям тела в эти моменты времени, векторы скорости $⃗v1$ и $⃗v2$ , отложим их изменение $ΔR⃗$ и $Δ⃗v$ и отметим равные углы.

В результате получим следующий рисунок:

$PIC$

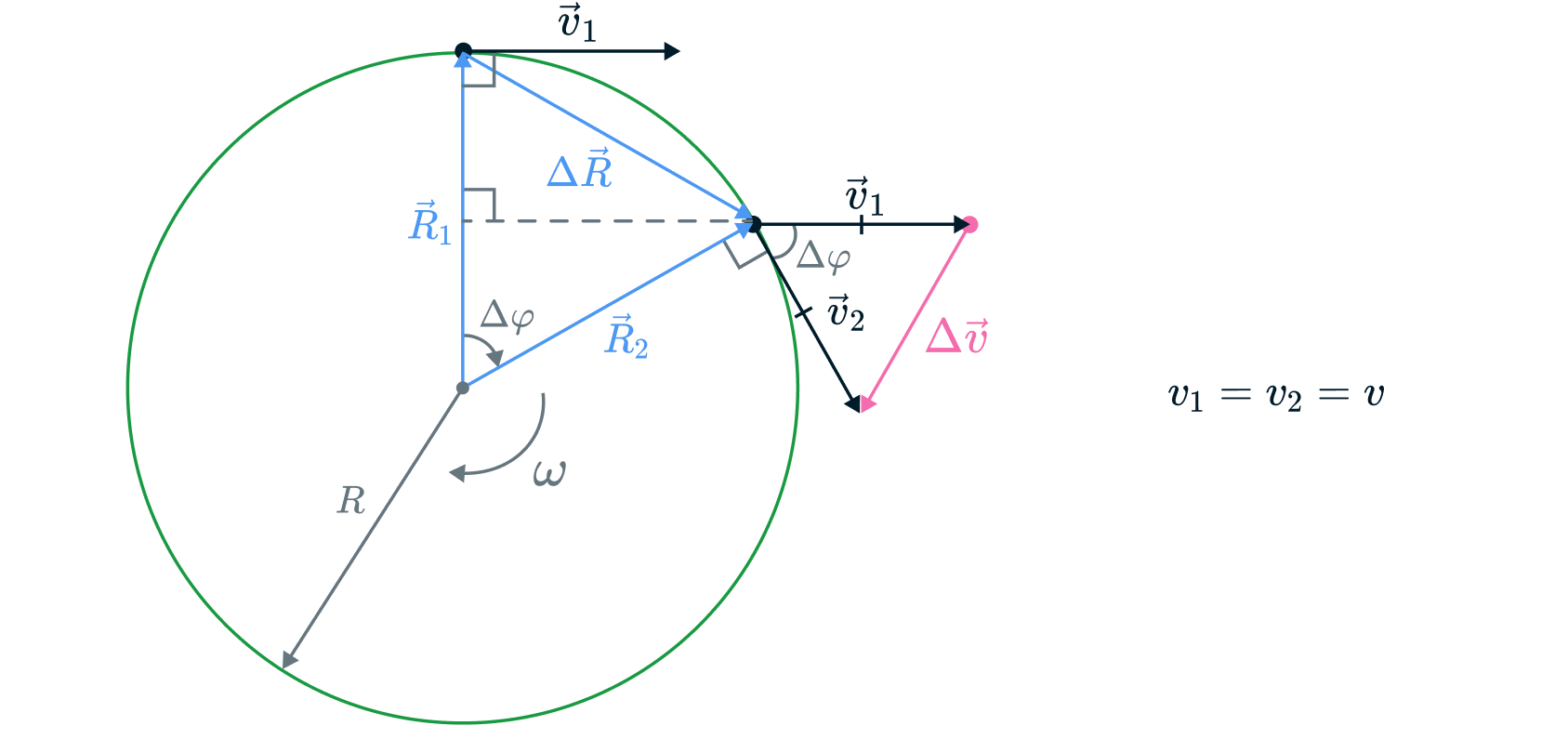
Вспомним, что поскольку движение по окружности равномерное, модуль линейной скорости постоянен. Поэтому:

v1 = v2 = v = const

Тогда заметим, что полученные векторные треугольники подобны. Действительно, $R1 =R2 = R$ , $v1 = v2$ , а также равны углы между соответствующими катетами. Тогда запишем подобие:

-R- = -v- ⇒ R-= ΔR- ΔR Δv v Δv

Разделим обе части полученного выражения на $Δt$ :

R-1--= ΔR-1--⇒ Δv-R-= ΔR- v Δt Δv Δt Δt v Δt

Заметим, что по определению скорость $v$ — это отношение изменения радиус-вектора $ΔR$ к изменению времени $Δt$ , а ускорение $a$ — отношение изменения вектора скорости $Δv$ к изменению времени $Δt$ . Учитывая это, перепишем имеющееся выражение:

R v2 a-v =v ⇒ a = R-

Осталось заметить, что полученное ускорение и является нормальным. Также, используя связь между угловой и линейной скоростями, получим второй вид этой формулы:

a= ω2R

Ускорение при криволинейном движении

Криволинейное движение — это движение, траектория которого представляет некоторую кривую. Чтобы описать такое движение, траектория рассматривается как набор участков окружностей.

$PIC$

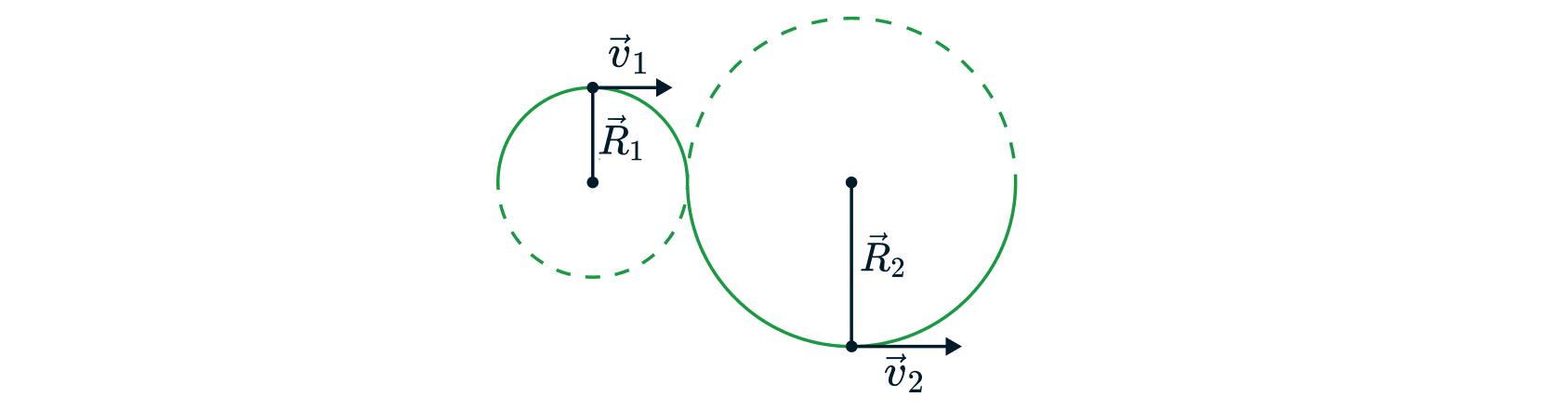
При этом, радиусы $R1$ и $R2$ называются радиусами кривизны траектории в соответствующих точках.

В общем случае при криволинейном движении скорость изменяется по величине и по направлению, поэтому полное ускорение имеет две компоненты — нормальное ускорение и тангенциальное ускорение. Рассмотрим их подробнее.

Нормальное ускорение — компонента ускорения, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной, направленное перпендикулярно (по нормали) вектору скорости к центру кривизны траектории.

2 an = v = ω2R R

Единицы измерения: $2 [an]= м/c$ (метр в секунду в квадрате).

Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения. Если модуль скорости увеличивается, то тангенциальное ускорение $aτ$ направлено по скорости, а если модуль уменьшается, то тангенциальное ускорение $aτ$ направлено против скорости.

a =v′(t) τ

Единицы измерения: $2 [aτ]= м/c$ (метр в секунду в квадрате).

Полное ускорение тела, движущегося по окружности, равно векторной сумме тангенциального и нормального ускорений.

⃗aполн = ⃗aτ + ⃗an

Если учесть, что $⃗an ⊥ ⃗aτ$ , то воспользовавшись теоремой Пифагора, получим:

∘ -2---2 aполн = an+ aτ

Кинематические соотношения при движении по окружности

Соотношение 1: диск

$PIC$

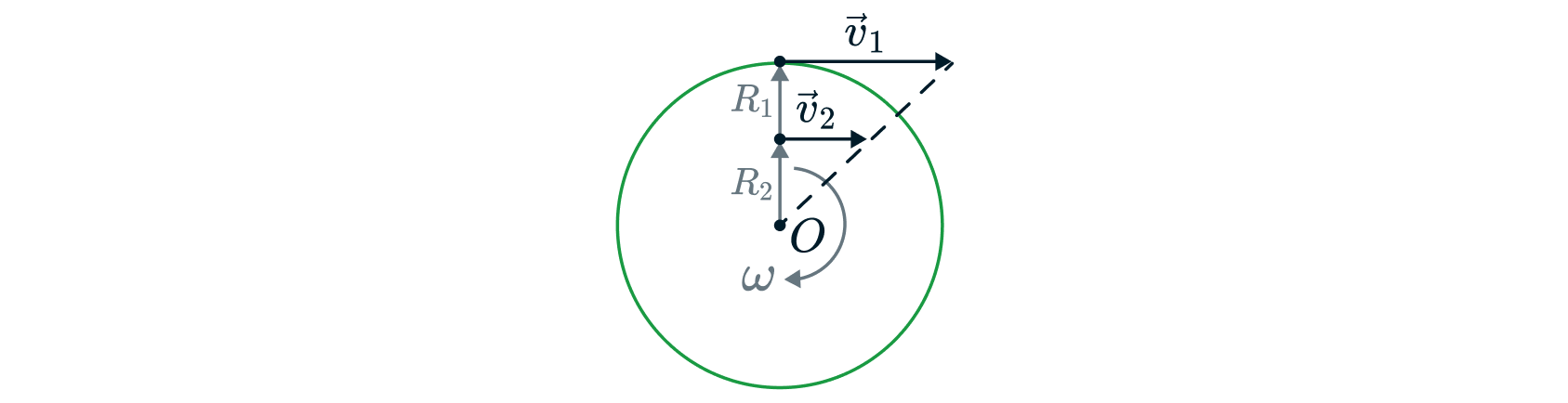
Все точки, принадлежащие одному и тому же диску, вращаются с одинаковой угловой скоростью:

ω1 = ω2

С учетом связи линейной и угловой скорости можно сделать вывод, что линейные скорости точек относятся прямо пропорционально их радиусам:

v = ωR ⇒ v1= R1- v2 R2

Из этого соотношения видно, что чем ближе точка к центру окружности, тем меньше ее линейная скорость.

Соотношение 2: ременная передача

$PIC$

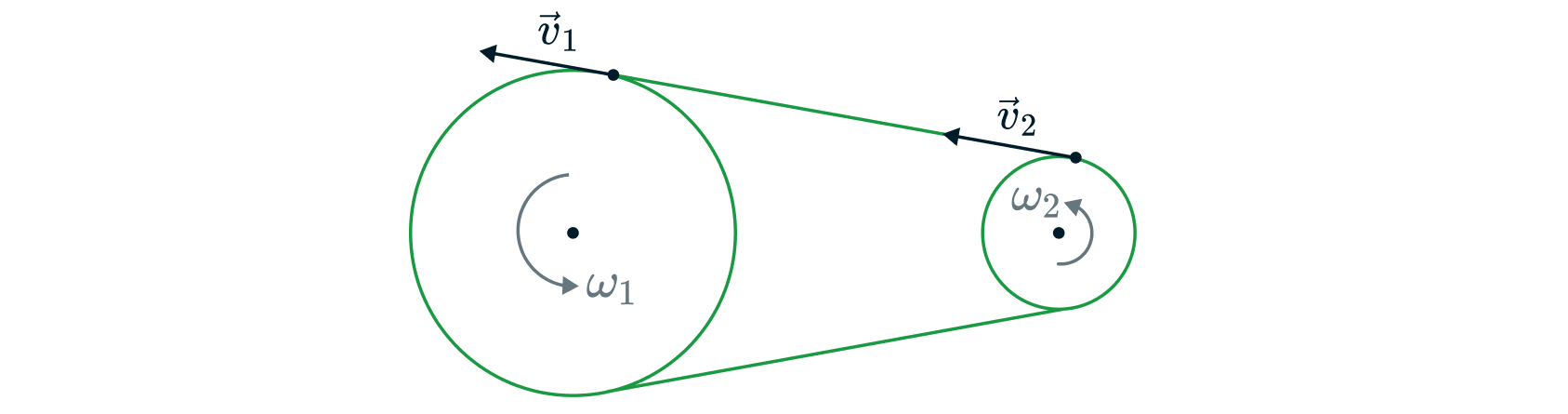
Поскольку шкивы соединены ремнем и ремень не растягивается и не сжимается, линейные скорости всех точек ремня одинаковы:

v1 = v2

При этом угловые скорости шкивов могут быть как разными $ω1 ⁄= ω2$ , так и одинаковыми $ω1 = ω2$ .

Соотношение 3: зубчатая передача

$PIC$

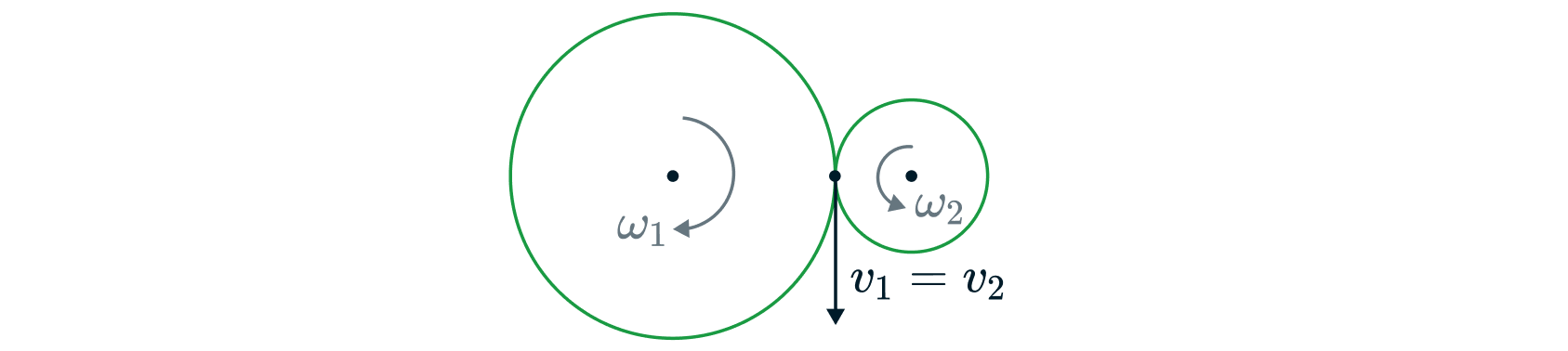
В точке контакта колес линейные скорости равны:

v1 = v2

При этом угловые скорости колес могут быть как разными $ω1 ⁄=ω2$ , так и одинаковыми $ω1 = ω2$ .

Примеры решения задач

Задача 1

Диск равномерно вращается и за время $t= 2$ мин совершает $N = 360$ оборотов.

Найдите:

1) Частоту вращения $ν$ ;

2) Угловую скорость вращения $ω$ ;

3) Период вращения диска $T$ ;

4) Линейную скорость $v1$ точек диска, расположенных на расстоянии $R1 = 0,2$ м от центра диска;

5) Ускорение $an$ точек диска, расположенных на расстоянии $R2 = 10$ см от центра диска.

Решение

Используя определение, найдем частоту:

ν = N-= 360--=3 об/с t 120 с

угловую скорость:

ω = 2π ν = 2π⋅3 с−1 ≈ 18,8 с−1

и период вращения:

T = 1= -t = 1 с≈ 0,33 с ν N 3

Используя связь линейной и угловой скоростей, а также формулу для нормального ускорения, найдем линейную скорость:

v1 = ωR1 = 18,8 с−1 ⋅0,2 м = 3,76 м/с

а также нормальное ускорение:

2 an = ω2R2 = (18,8 с−1)2⋅0,1 м ≈ 35,3 м/ с

Задача 2

Космонавт на тренировке, сидя в центрифуге, вращается по окружности радиуса 100 м, причем его скорость меняется по закону: $v(t)= 3t$ . Найдите полное ускорение, которое испытывает космонавт через 20 секунд после начала тренировки.

$PIC$

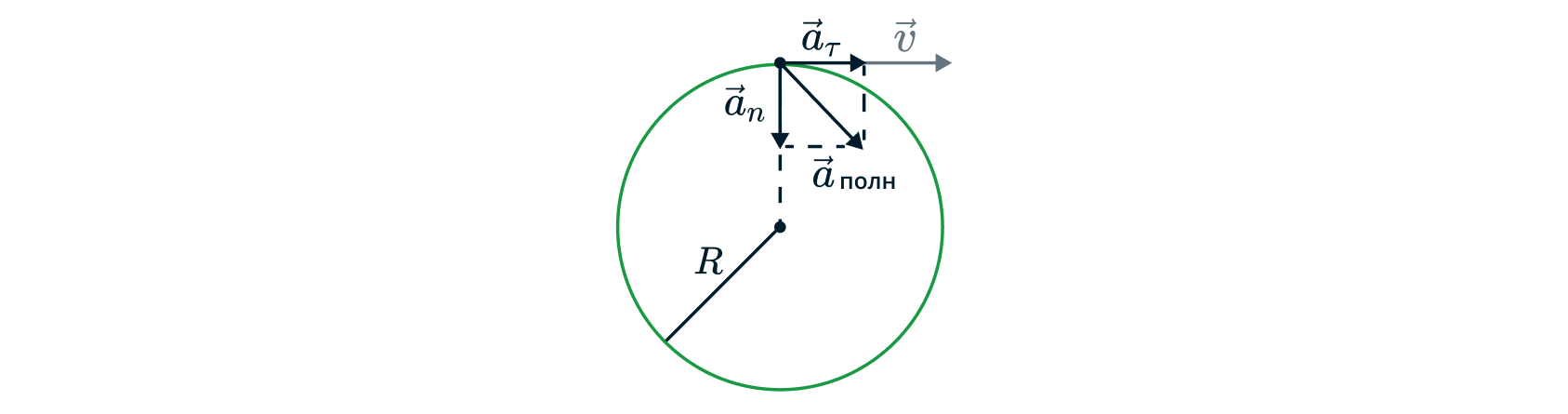
Решение

Заметим, что модуль скорости меняется в зависимости от времени — это значит, что появляется тангенциальное ускорение. Так как космонавт движется по окружности, то возникает и центростремительное ускорение. Теперь, когда мы знаем какие компоненты ускорения присутствуют в задаче, можем перейти к вычислениям. Скорость через 20 секунд:

v(τ) = 3τ = 3⋅20= 60 м/c

Тогда нормальное ускорение в этот момент времени будет равно:

2 2 2 an = v-= 60- = 36 м/ с R 100

Тангенциальное ускорение соответственно равно:

′ 2 aτ = v (t)= 3 м/c

В конечном итоге вычисляем полное ускорение через теорему Пифагора:

aполн = ∘a2n+-a2τ = ∘362-+-32 ≈ 36,12 м/c2

Предыдущая справка

Следующая справка