Работа. Энергия. Закон сохранения энергии
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#606
Основные формулы
Импульс тела:
|
|
Работа силы:
|
|
Мощность:
|
|
Мгновенная мощность:
|
|
Коэффициент полезного действия (КПД):
|
|
Кинетическая энергия:
|
|
Теорема о кинетической энергии:
|
|
Теорема о потенциальной энергии:
|
|
Закон сохранения полной механической энергии:
|
|
Работа силы тяжести:
|
|
Работа силы упругости:
|
|
Потенциальная энергия силы тяжести:
|
|
Потенциальная энергия силы упругости:
|
|
Потенциальная энергия силы гравитации:
|
|
Потенциальная энергия силы Кулона:
|
|
Основные понятия
Работа силы
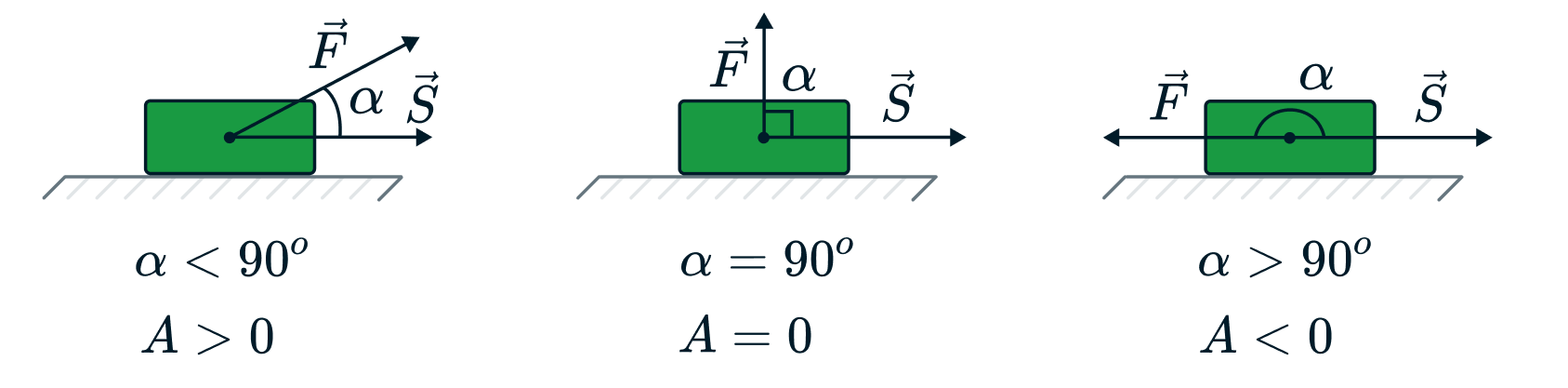
Работа силы — это величина, определяемая как скалярное произведение вектора силы на вектор перемещения. Раскрыв скалярное произведение, получим, что работа силы — это произведение модуля вектора силы на модуль вектора перемещения и на косинус угла между ними.

|
|
Единицы измерения:
= Н
м = Дж — джоуль.
Из-за наличия скалярного произведения появляется зависимость работы от направления силы:
Мощность
Мощность — это скалярная величина, характеризующая скорость совершения работы. Она равняется отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
|
|
Единицы измерения:
Вт — ватт.
При неизменной силе справедливы следующие рассуждения:
запишем выражения для работы и мощности:
|
|
Подставляя выражение работы в выражение мощности, имеем:
|
|
По определению , следовательно, мгновенная мощность может быть
выражена следующим образом:
|
|
Коэффициент полезного действия
Коэффициент полезного действия (КПД) — это физическая величина, равная отношению полезной работы к затраченной. Часто эту величину домножают на 100, чтобы работать с процентами.
|
|

Единицы измерения:
— проценты, однако также используются доли единицы (для
перевода в доли единицы необходимо проценты поделить на 100
).
КПД показывает, какая часть полученной системой энергии переводится в
полезную работу. При этом у полезной работы нет строгого определения,
однако в задачах полезной работой чаще всего является нагрев/охлаждение и
подъем/перемещение тел. По определению КПД не может быть больше 1
(100).
Силы в природе
Силы в природе можно классифицировать на два вида:
-
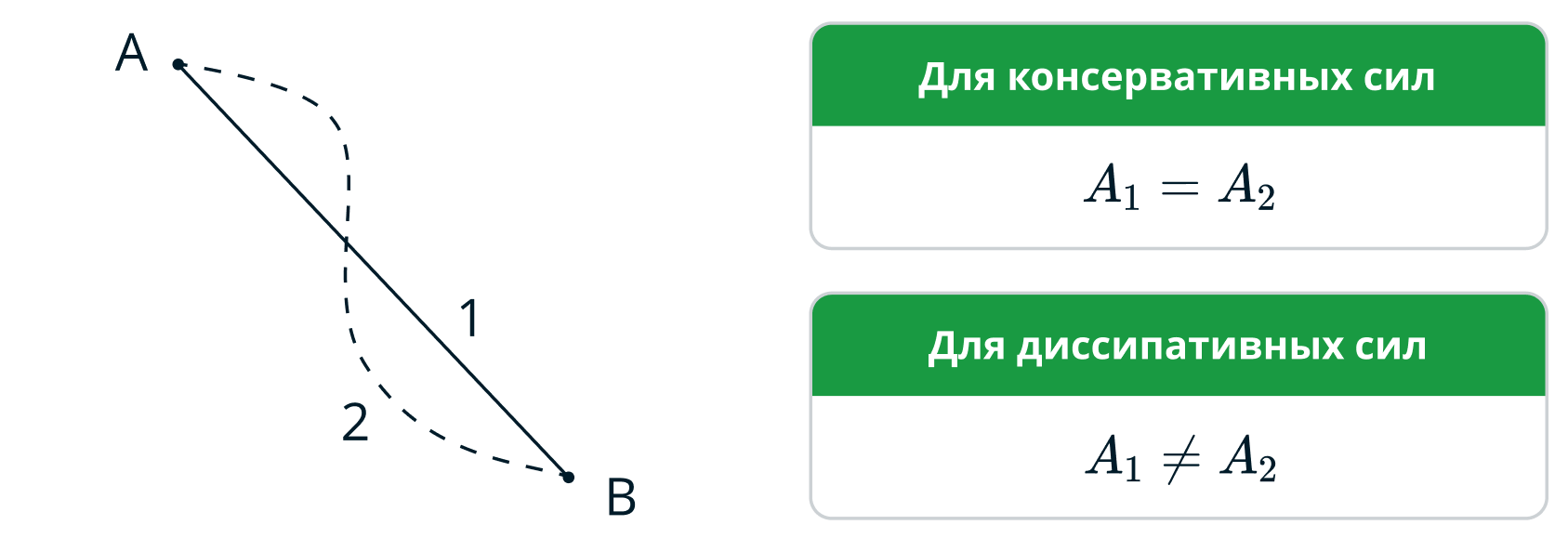
Консервативные (потенциальные) силы — силы, сохраняющие механическую энергию замкнутой системы тел. Работа консервативных сил не зависит от формы пути между двумя точками (при перемещении тела между ними), а зависит лишь от начального и конечного положения тела. Работа потенциальной силы по замкнутой траектории равна нулю.
Примеры: сила тяжести, сила упругости, сила гравитации, сила Кулона.
-
Диссипативные (непотенциальные) силы — силы, которые рассеивают механическую энергию. Работа диссипативной силы зависит от траектории движения тела и по замкнутой траектории не равна нулю.
Примеры: сила трения, сила сопротивления, сила натяжения.
Энергия
Кинетическая энергия
Кинетическая энергия — это энергия механического движения тела. Она определяется по следующей формуле:
|
|
Единицы измерения:
Дж — джоуль.
Зная, что импульс , а также домножив и поделив на
, имеем другой
вид формулы кинетической энергии:
|
|
При этом справедлива теорема об изменении кинетической энергии, которая звучит так:
Изменение кинетической энергии тела равно работе всех сил, действующих на тело.
|
|
Потенциальная энергия
Для потенциальных сил вводят скалярную величину — потенциальную энергию. Она зависит от взаимного положения тел в системе, которое изменяют консервативные силы. Сопоставим каждой потенциальной силе ее энергию:
Единицы измерения:
Дж — джоуль.
Величина потенциальной энергии может быть определена с точностью до произвольной постоянной, значение которой зависит от выбора нулевого уровня. Нулевой уровень — положение тела, в котором потенциальную энергию, которой оно обладает, условно принимают за ноль.
В отличие от кинетической энергии, потенциальная энергия может принимать отрицательные значения, если тело находится ниже нулевого уровня.
Теорема о потенциальной энергии
Работа потенциальной силы определяется как разность потенциальных энергий (начальная энергия минус конечная)
|
|
Рассмотрим, как работает данная теорема на примере силы тяжести. Пусть
тело массой переместилось из положения 1 в положение 2 как показано
на рисунке.
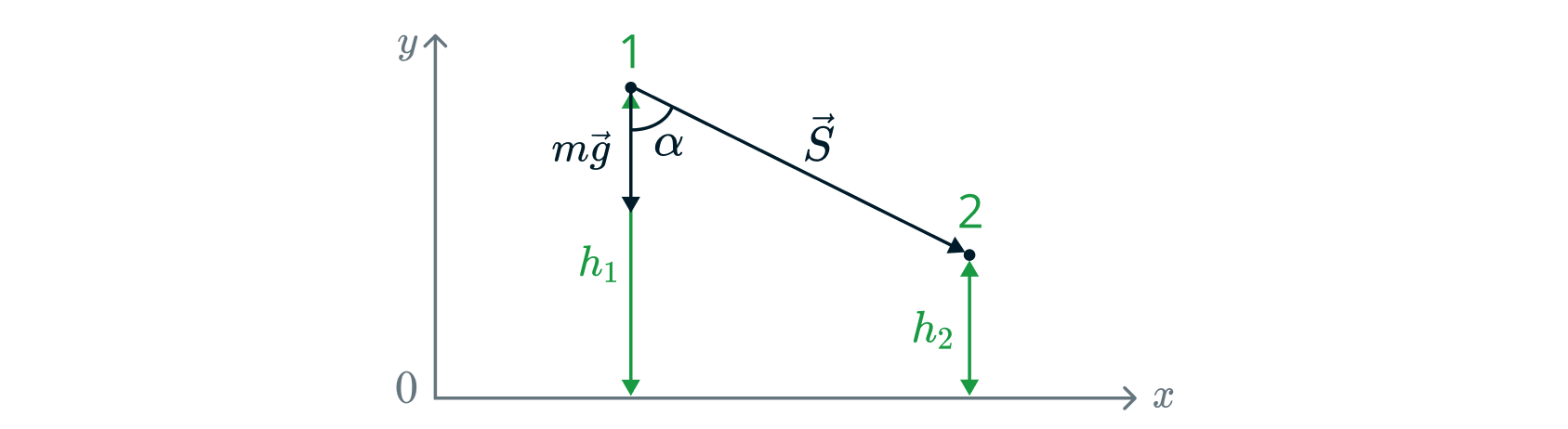
Работу силы тяжести в положении 1 можно найти по уже известной нам формуле:
|
|
Теперь воспользуемся теоремой о потенциальной энергии и найдем работу
той же силы тяжести с учетом того, что :
|
|
Также можно заметить, что :
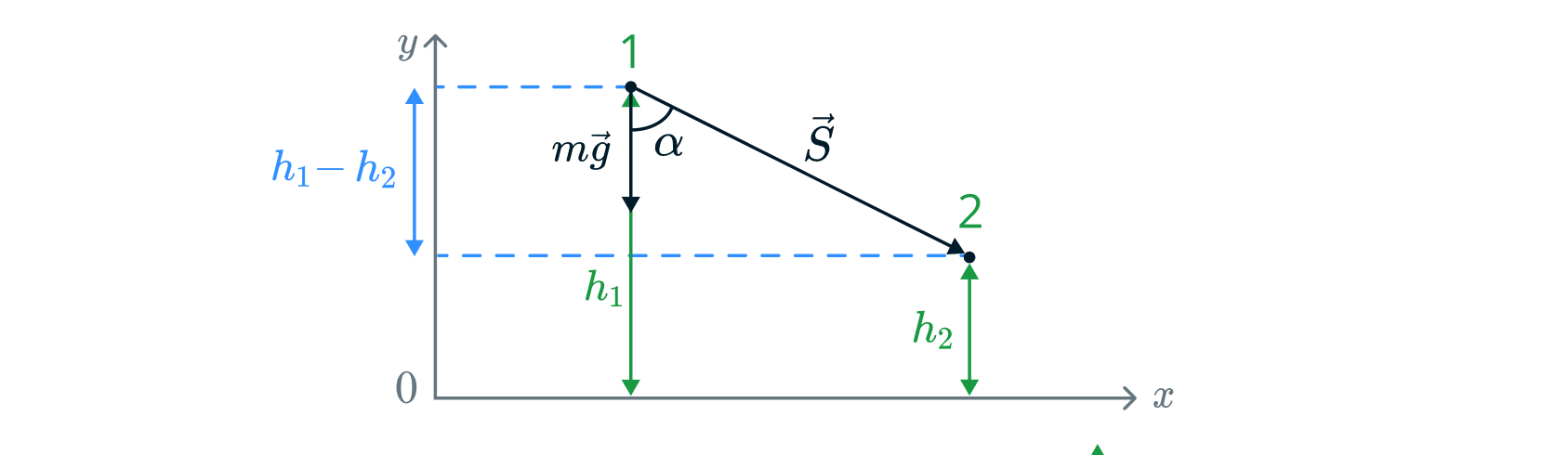
Тогда формула упростится:
|
|
Закон сохранения механической энергии
Вспомним теорему об изменении кинетической энергии:
|
|
Разобьем сумму на две: сумму потенциальных и непотенциальных сил:
|
|
Пусть сумма работ всех непотенциальных сил равна нулю:
|
|
Вспомним теорему о потенциальной энергии и подставим
ее в предыдущее выражение:
|
|
Мы получили закон сохранения механической энергии:
|
|
Формулировка: сумма кинетической и потенциальной энергии в конце равна сумме кинетической и потенциальной энергии в начале и есть величина неизменная в том случае, если работа всех непотенциальных сил равна нулю.
Важные конструкции с ЗСЭ
Шарик, подвешенный на нити, совершает полный оборот с минимальной скоростью
Необходимо определить, с какой минимальной скоростью шарик, подвешенный на нити, сможет совершить полный оборот.
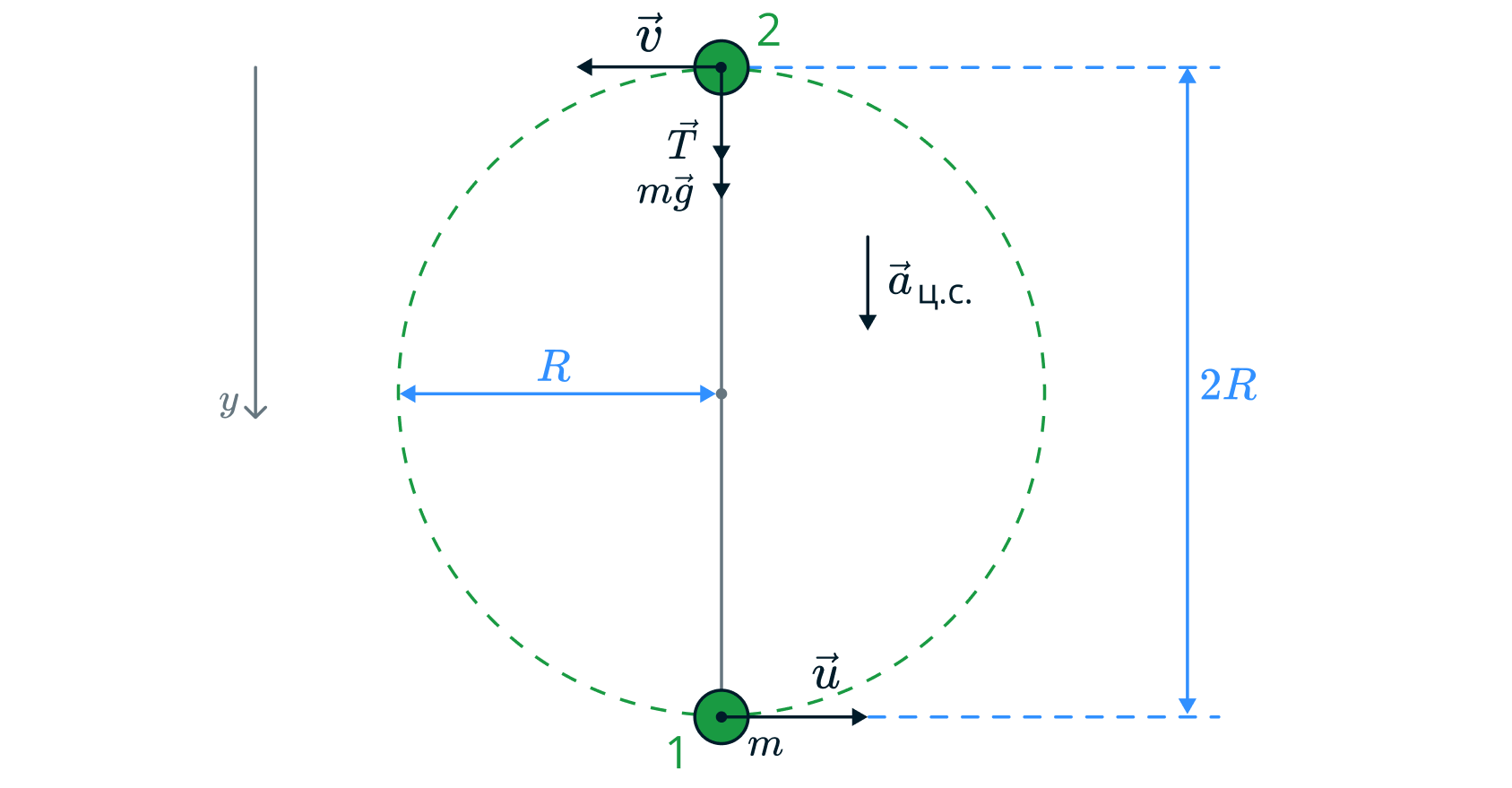
Пусть при прохождении положения 1 шарик массой имеет скорость
.
Рассмотрим положение 2. В верхней точке (положение 2) на шарик действует
сила натяжения нити и сила тяжести. Так как траектория движения —
окружность, то присутствует центростремительное ускорение. Для
совершения полного оборота шарику необходимо обладать некоторой
скоростью в верхней точке (положение 2). В противном случае, если его
скорость в положении 2 равна нулю, шарик упадет вниз. Примем скорость
шарика в верхней точке за
. Запишем второй закон Ньютона для шарика в
положении 2 и спроецируем его на ось
:
|
|
Рассмотрим энергии, которыми обладает шарик в положениях 1 и 2. Примем,
что нулевой уровень потенциальной энергии проходит через точку 1, как
показано на рисунке. Тогда в положении 1 шарик будет обладать только
кинетической энергией. В положении 2 шарик находится на высоте
относительно выбранного нами нулевого уровня и обладает скоростью
,
следовательно, он обладает потенциальной и кинетической энергиями.
Запишем закон сохранения энергии для шарика в положениях 1 и
2:
|
|
Из ЗСЭ следует, что чем меньше скорость , тем меньше скорость
. Из
второго закона Ньютона следует, что чем меньше скорость
, тем
меньше сила натяжения нити
. Чтобы тело совершило полный
оборот, сила натяжения нити должна быть минимальна в верхней точке
(положение 2) и во всех положениях должна быть
. Так как нас
интересует минимальная скорость, то и значение
должно быть
минимальным
— предельный случай, то есть сила натяжения нити
отсутствует.
Учтем этот случай при записи второго закона Ньютона для положения 2:
|
|
Поделим на и домножим на 2 выражение для ЗСЭ, а также учтем, что
:
|
|
Это и есть минимальная скорость, необходимая для того, чтобы шарик на нити сделал полный оборот.
Шарик, закрепленный на стержне, совершает полный оборот с минимальной скоростью
ЗСЭ для стержня выглядит аналогично ЗСЭ для нити:
|
|
В данном случае минимальная скорость в положении 2 равна нулю.
Тогда:
|
|
Минимальная скорость, которая необходима для того чтобы шарик,
закрепленный на стержне, совершил полный оборот: .
|
|
В отличие от нити стержень является жесткой конструкцией, и сила натяжения может действовать как вниз, так и вверх, поэтому условия минимальности для стержня и нити разные.
Шарик на нити отклоняют от положения равновесия
Рассмотрим следующую мини-конструкцию. Пусть шарик массой ,
подвешенный на нити длиной
, имеет скорость
в положении
(положение равновесия) и поднимается в положение
, где его скорость
, отклонившись на угол
от положения равновесия.
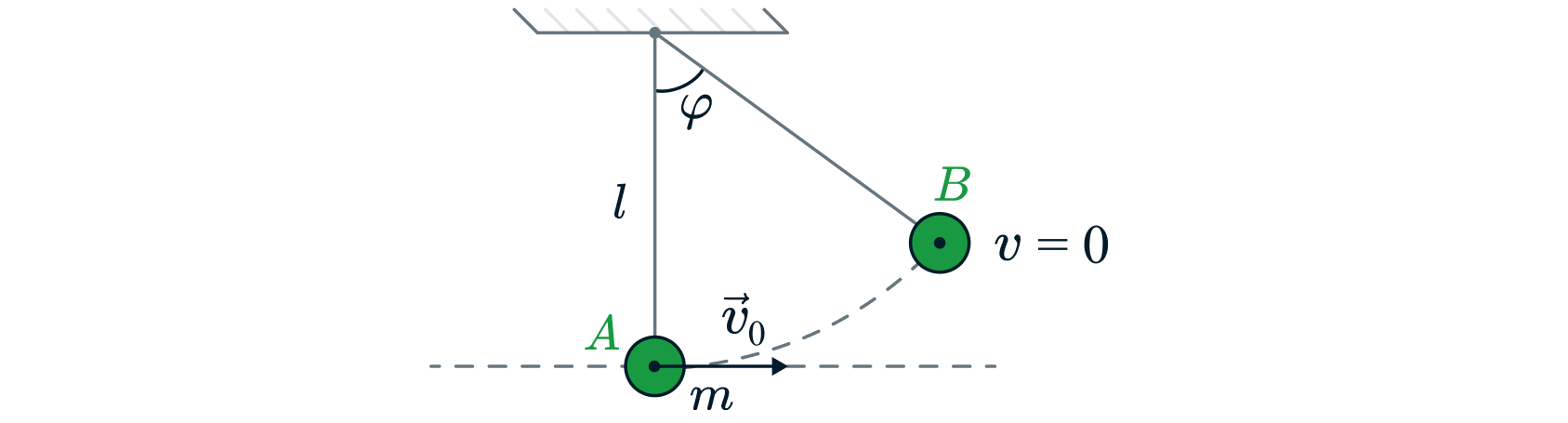
Пусть нулевой уровень для потенциальной энергии шарика проходит через
точку как показано на рисунке. Тогда в положении
шарик обладал
только кинетической энергией. При переходе из положения
в положение
шарик поднимается на некоторую высоту
, где его скорость становится
равной нулю. Следовательно, в положении
шарик обладает только
потенциальной энергией. Исходя из этого запишем закон сохранения
энергии:
|
|
Выразим высоту . Для этого рассмотрим прямоугольный треугольник,
который на рисунке ниже показан синим цветом.
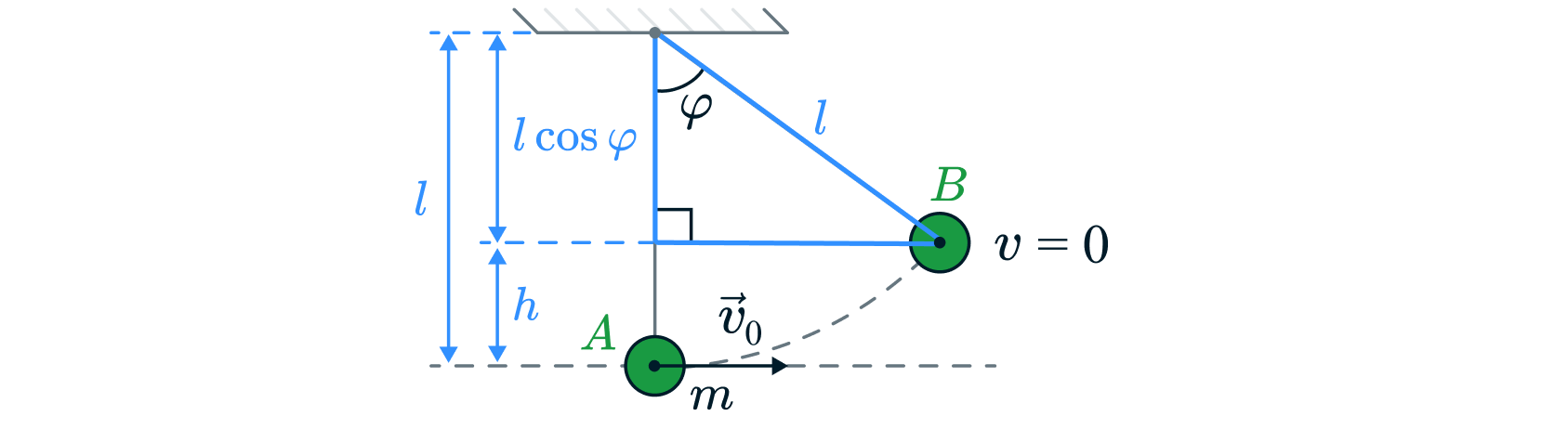
Тогда высоту можно найти как:
|
|
Подставим в предыдущую формулу и найдем связь между тремя
параметрами (,
,
):
|
|
