Механика

Импульс. Закон сохранения импульса

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Механика

Теоретическая справка

#607

Основные формулы

Импульс тела:

⃗p =m ⃗v

Второй закон Ньютона:

Δ⃗p =(⃗F1+ F⃗2+ ⋅⋅⋅+F⃗n )Δt

Закон сохранения импульса двух тел:

⃗p1+ ⃗p2 = ⃗p′1+ ⃗p′2

Основные понятия

Импульс тела — векторная физическая величина, численно равная произведению массы тела на его скорость. Импульс — это количественная характеристика движения.

⃗p =m ⃗v

Единицы измерения:

$[p]=$ кг $⋅$ м/с

Второй закон Ньютона в импульсной форме

Запишем второй закон Ньютона согласно основной его формулировке:

⃗F1+ ⃗F2+ ...+F⃗n = m⃗a

Распишем ускорение по определению:

Δ⃗v ⃗F1+ ⃗F2+ ...+F⃗n = m Δt-

Рассмотрим отдельно правую часть. Распишем изменение скорости и раскроем скобки:

Δ ⃗v m (⃗v − ⃗v) m⃗v − m ⃗v m Δt-= ----кΔt-0- = --кΔt---0

При этом заметим, что $m⃗vк$ и $m ⃗v0$ — это конечный и начальный импульс системы:

⃗F1+ ⃗F2+ ...+ ⃗Fn = ⃗pк−-⃗p0 Δt

Тогда заменяя $⃗pк− ⃗p0 = Δ ⃗p$ , получим:

⃗F1+ ⃗F2+ ...+F⃗n = Δ-⃗p ⇒ Δ ⃗p= (⃗F1+ ⃗F2+ ...+F⃗n )Δt Δt

Таким образом, второй закон Ньютона в импульсной форме имеет следующий вид:

Δ⃗p = ⃗FΔt

где выражение $⃗ F Δt$ называется импульсом силы.

Импульс системы тел

Рассмотрим систему из трех тел 1, 2, 3. Пусть все тела системы взаимодействуют друг с другом с некоторыми силами $⃗F12$ , $⃗F13$ , $⃗F21$ , $⃗F23$ и $⃗ F31$ , $⃗ F32$ .

$PIC$

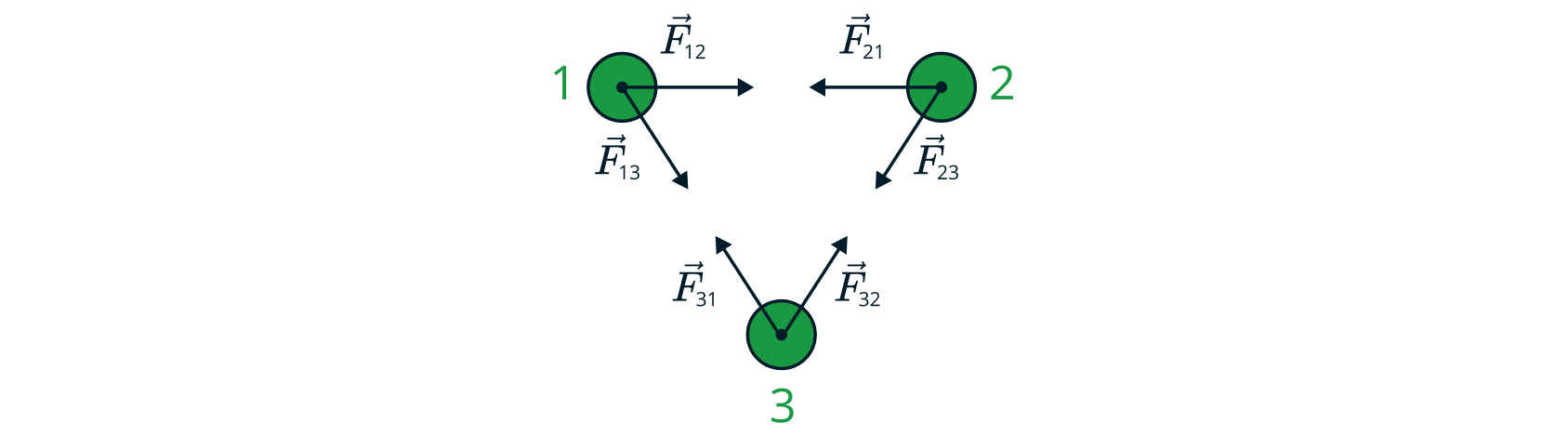
Выделим подсистему, состоящую из тел 1 и 2 и разделим силы на два вида: внутренние — силы, которые появляются в результате взаимодействия тел внутри системы, и внешние — силы, которые действуют на тела системы со стороны внешних объектов. В данном случае $F⃗12$ и $⃗F21$ — внутренние силы, $F⃗13$ , $⃗F23$ — внешние.

$PIC$

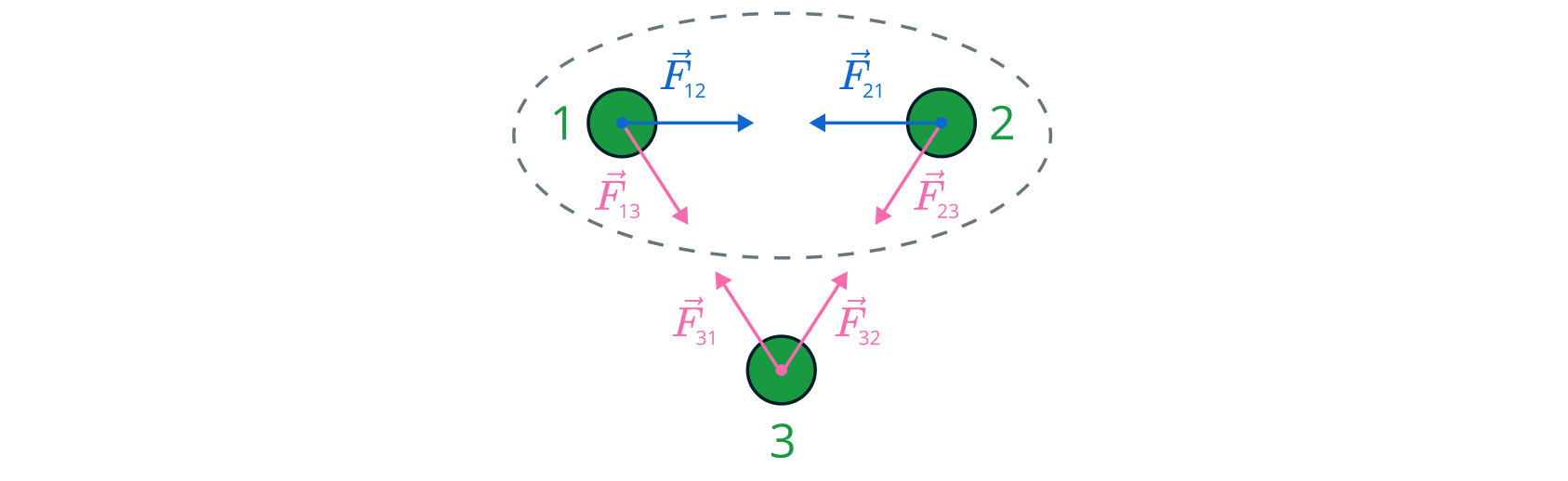
Запишем второй закон Ньютона в импульсной форме для обоих тел. Для первого тела имеем:

Δ⃗p1 = (⃗F12+ ⃗F13)Δt

Аналогично для второго тела:

Δ⃗p2 = (⃗F21+ ⃗F23)Δt

Тогда суммируя эти уравнения, получим:

Δ ⃗p1+ Δ⃗p2 = (⃗F12+ ⃗F13 +F⃗21+ ⃗F23)Δt

По третьему закону Ньютона векторная сумма внутренних сил $⃗F12$ и $⃗F21$ равна нулю. Также назовем величину $Δ ⃗p1+ Δ⃗p2$ изменением импульса системы $Δ ⃗pсист$ . С учетом этого:

Δ⃗pсист = (⃗F13+ ⃗F23)Δt

Видно, что изменение импульса системы равно векторной сумме импульсов внешних сил. В общем виде это утверждение записывают так:

∑ Δ⃗pсист = ⃗FвнешΔt

Закон сохранения импульса

Проанализируем полученное выражение. Оно примечательно тем, что определяет изменение импульса системы тел через внешние силы и время взаимодействия. Существуют ситуации, в которых изменение импульса становится равным нулю, а значит импульс системы не меняется — выполняется закон сохранения импульса. Это происходит если:

векторная сумма внешних сил, действующих на систему, равна нулю. В таком случае $∑ ⃗F =0 внеш$ , из чего следует, что $Δ ⃗p = 0 сист$
сумма проекций векторов внешних сил, действующих на систему тел, на некоторую ось $x$ равна нулю $∑ ⃗Fxвнеш = 0$ . Тогда импульс системы остается неизменным вдоль этой оси $Δ ⃗pxсист =0$
время взаимодействия $Δt$ мало, поэтому суммарный импульс внешних сил за время взаимодействия во много раз меньше импульса системы $||∑ || | F⃗внеш|Δt≪ |⃗pсист|$ . Согласно полученному равенству, получаем: $Δ ⃗pсист ≪ ⃗pсист$ . Это значит, что изменение импульса много меньше, чем сам импульс, поэтому таким изменением можно пренебречь: $Δ⃗pсист = 0$

Закон сохранения импульса системы: вектор импульса системы тел постоянен, если векторная сумма внешних сил, действующих на систему, равна нулю, либо время взаимодействия пренебрежимо мало.

Δ ⃗pсист = ⃗0 ⇒ ⃗pсист = const

Предыдущая справка

Следующая справка