Механика

Давление. Сила Архимеда

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Механика

Теоретическая справка

#608

Основные формулы

Давление:

p = F- S

Давление жидкости на дно сосуда:

p = ρжgh

Сила давления:

F = pS

Сила Архимеда для ИСО:

FАрх = ρжgVп.ч.

Основные понятия

Понятия давления и силы давления

Давление — это физическая величина, численно равная отношению силы $F$ , действующей перпендикулярно поверхности к площади этой поверхности $S$ .

F p = S-

Единицы измерения в системе СИ: $[p]=$ Н/м $2$ $= 1$ Па (паскаль).

Существуют и другие единицы измерения давления, не входящие в систему СИ:

$[p]=1$ мм. рт. ст. (миллиметр ртутного столба) $≈ 133,3$ Па. Также давление измеряется в атмосферах:

$[p]=1$ атм (атмосфера) $5 ≈ 10$ Па.

Давление столба жидкости. Сила давления

Давление столба жидкости на дно сосуда

Получим выражение для давления столба жидкости на дно сосуда:

Имеется сосуд с площадью дна $S$ , заполненный жидкостью до высоты $h$ .

$PIC$

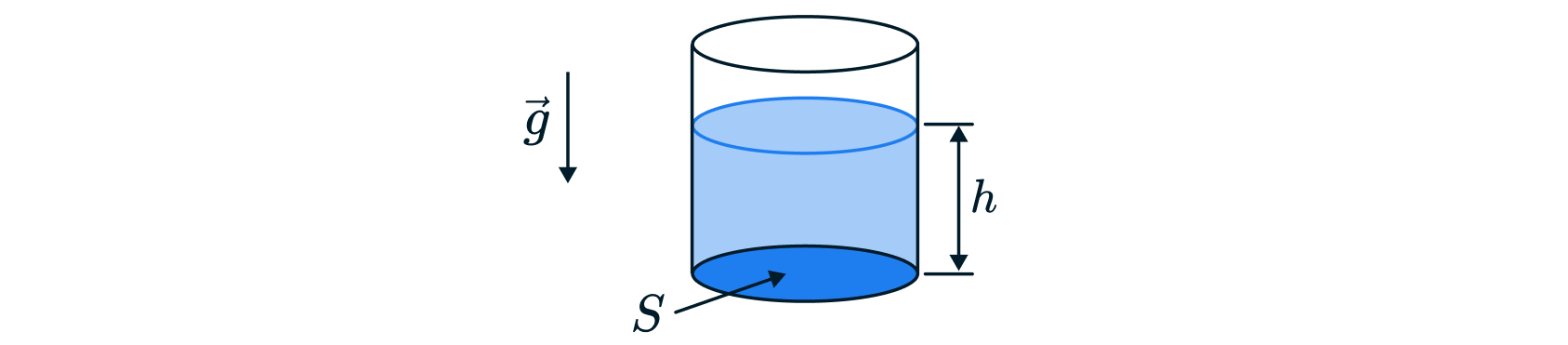
На дно сосуда площадью $S$ действует сила — вес жидкости $P$ . Найдем давление на дно сосуда:

p = P- S

Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести:

P = mg

Массу жидкости можно выразить через ее плотность $ρ ж$ и объем $V$ :

m = ρж ⋅V

Из геометрии объем жидкости $V$ :

V = Sh

Подставим в выражение для давления $p$ вес жидкости, выраженный через известные нам параметры системы $S,$ $h,$ $ρ ж$ :

p= ρжShg- ⇒ p =ρжgh S

Давление, создаваемое слоем жидкости на дно и стенки сосуда прямо пропорционально высоте слоя жидкости $h$ , и ее плотности $ρж$ . Обратите внимание: давление не зависит от массы жидкости $m$ и от формы сосуда $S$ .

Получили важный результат — формулу для нахождения давления столба жидкости на дно сосуда:

p = ρжgh

Здесь $ρ ж$ — плотность жидкости, $g$ — ускорение свободного падения, $h$ — высота столба жидкости.

Сила давления — сила, действующая перпендикулярно поверхности тела, равная произведению давления на площадь этой поверхности.

F = p⋅S

Единицы измерения: $[F]= 1$ Н (ньютон).

$PIC$

Пусть дано три сосуда разной формы, заполненные одинаковой жидкостью до уровня $h$ . Запишем выражения для сил давления $F1$ , $F2$ , $F3$ действующих на дно этих сосудов:

F1 = p1 ⋅S1 = ρжghS1

F2 = p2 ⋅S2 = ρжghS2

F3 = p3 ⋅S3 = ρжghS3

Так как давление столба жидкости зависит только от плотности жидкости $ρж$ и высоты $h$ , получаем:

F1 :F2 :F3 = S1 :S2 :S3

Сила давления жидкости на дно сосуда зависит от площади основания этого сосуда.

Закон Паскаля

Формулировка закона

Давление, оказываемое на жидкость или газ, передается в любую точку системы (жидкости или газа) одинаково по всем направлениям.

Закон Паскаля лежит в основе устройства гидравлических машин. Изучим его применение подробнее:

Применение закона Паскаля

Гидравлический пресс — устройство, дающее выигрыш в силе. Состоит из поршней большого и малого диаметров, установленных в сообщающихся цилиндрах, под поршнями находится жидкость.

$PIC$

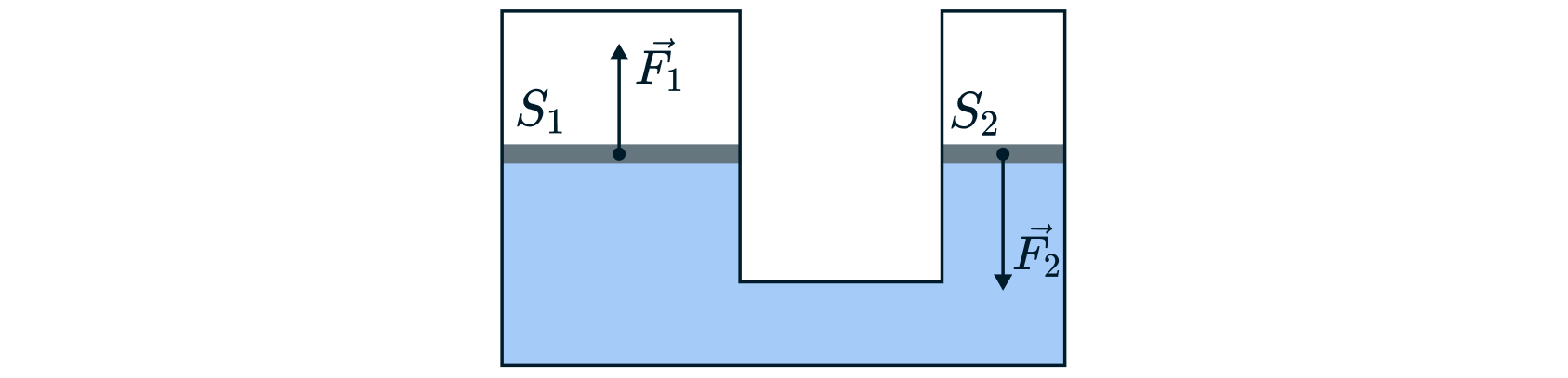
На поршень большего диаметра начинают действовать силой $F1$ , создавая давление $p = F1∕S1$ . Избыточное давление $p$ , согласно закону Паскаля, распространяется равномерно во все стороны, создавая на поршне малого диаметра точно такое же давление $p =F2∕S2$ . Из равенства давлений на поршнях можно вывести соотношение:

$F1 F2 F2 S2 S1 = S2 ⇒ F1 = S1$

Это соотношение называется «формулой гидравлического пресса».
Примером еще одной физической системы, в основе которой лежит закон Паскаля, являются сообщающиеся сосуды:
Сообщающиеся сосуды — любые два или несколько соединенных между собой сосудов, в которых жидкость может свободно перетекать из одного сосуда в другой. Для простоты далее будем рассматривать систему из двух соединенных сосудов.
Система может быть как однородной, так и включать в себя жидкости разного рода (то есть разной плотности $ρ 1$ и $ρ 2$ ). Рассмотрим устройство каждой системы:
1. Однородная жидкость устанавливается на одном уровне независимо от формы сосуда (при условии, что давление над жидкостью в сосудах одинаково).

$PIC$

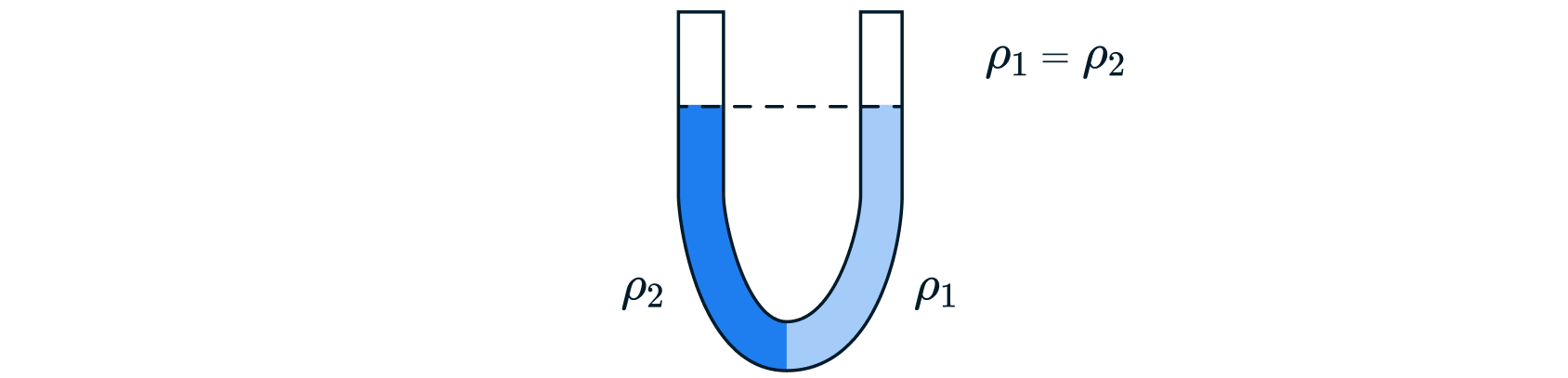
Из закона Паскаля, давление столба жидкости в левой части сообщающегося сосуда $p1$ равно давлению правого столба $p2$ .

$p1 =p2 ⇒ ρжgh1 = ρжgh2 ⇒ h1 = h2$

2. Неоднородная жидкость устанавливается на разных уровнях. Высоты столбов жидкостей обратно пропорциональны их плотностям:

$PIC$

$ρ1 h2 p1 = p2 ⇒ ρ1gh1 =ρ2gh2 ⇒ ρ2 = h1,$

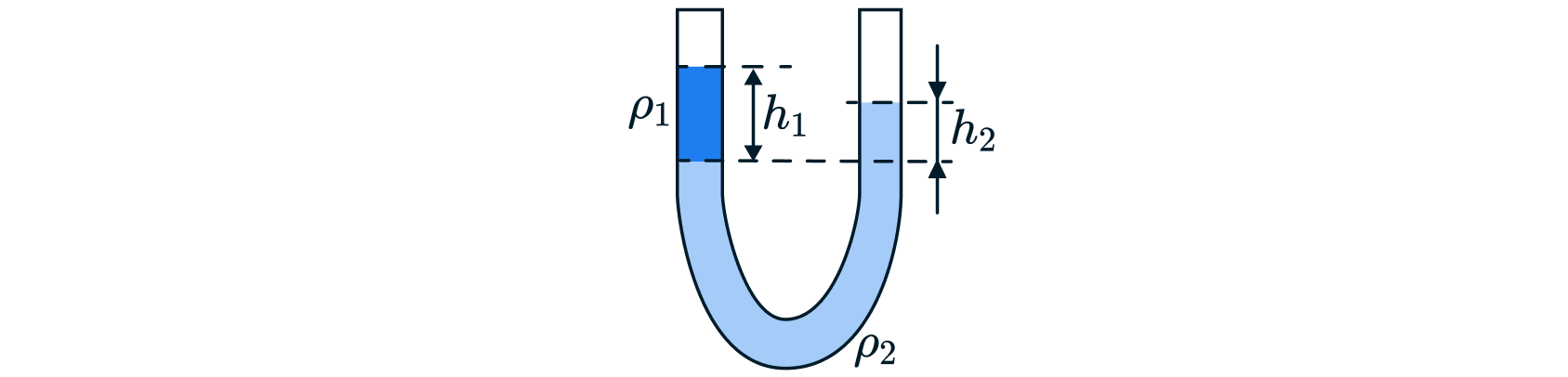
где $p1$ и $p2$ — давление столба жидкости в первом и втором колене сосуда соответственно.

Сила Архимеда

Формулировка закон Архимеда

На тело, погруженное в жидкость или газ, действует выталкивающая сила, численно равная весу объема жидкости или газа, вытесненного телом.

Эта выталкивающая сила называется силой Архимеда.

Вывод формулы

Получим выражение для Силы Архимеда, действующей на тело.

Сила Архимеда не должна зависеть от свойств тела, поскольку она действует на тело со стороны жидкости. Рассмотрим два случая:

Случай 1. Пусть имеется свинцовое и стальное тело произвольной одинаковой формы и два одинаковых сосуда с жидкостью.

$PIC$

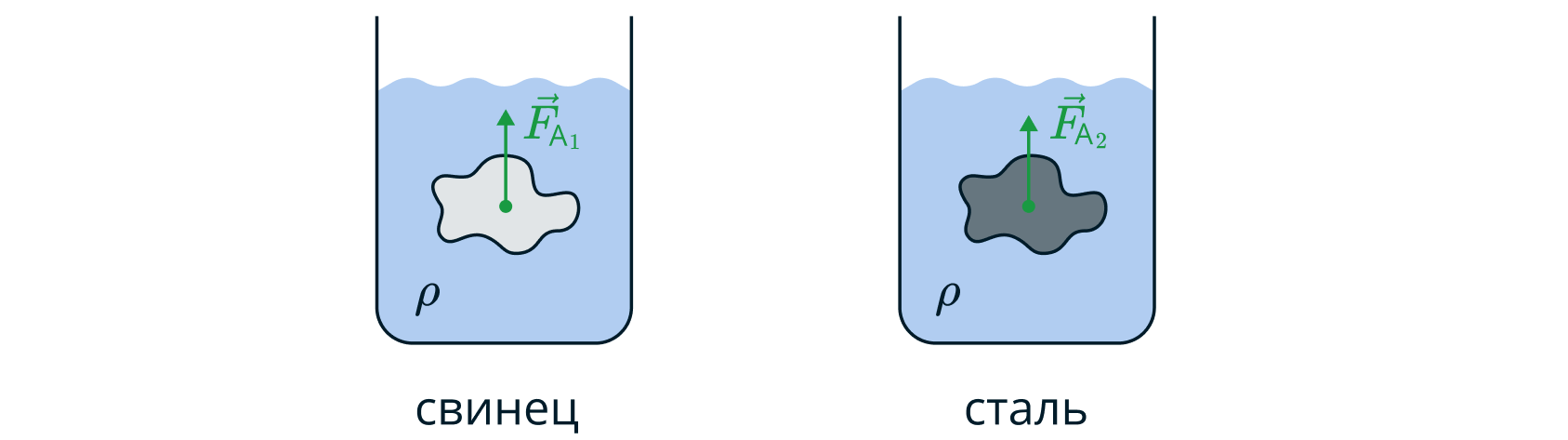
Силы Архимеда $⃗ FA1$ и $⃗ FA2$ , действующие на тело из свинца и на тело из стали равны, так как сила Архимеда определяется разностью давлений со стороны жидкости и не зависит от материала, из которого состоит тело. Итак, $FA1 =FA2$ .
Случай 2. Представим, что теперь некоторое тело погружено в жидкость лишь на некоторую часть (обозначим объем погруженной в воду части тела $Vп.ч.$ ). Пусть тело находится в равновесии, тогда на него действуют сила тяжести $m ч⃗g$ и сила Архимеда $⃗FA3$ , как показано на рисунке ниже.

$PIC$

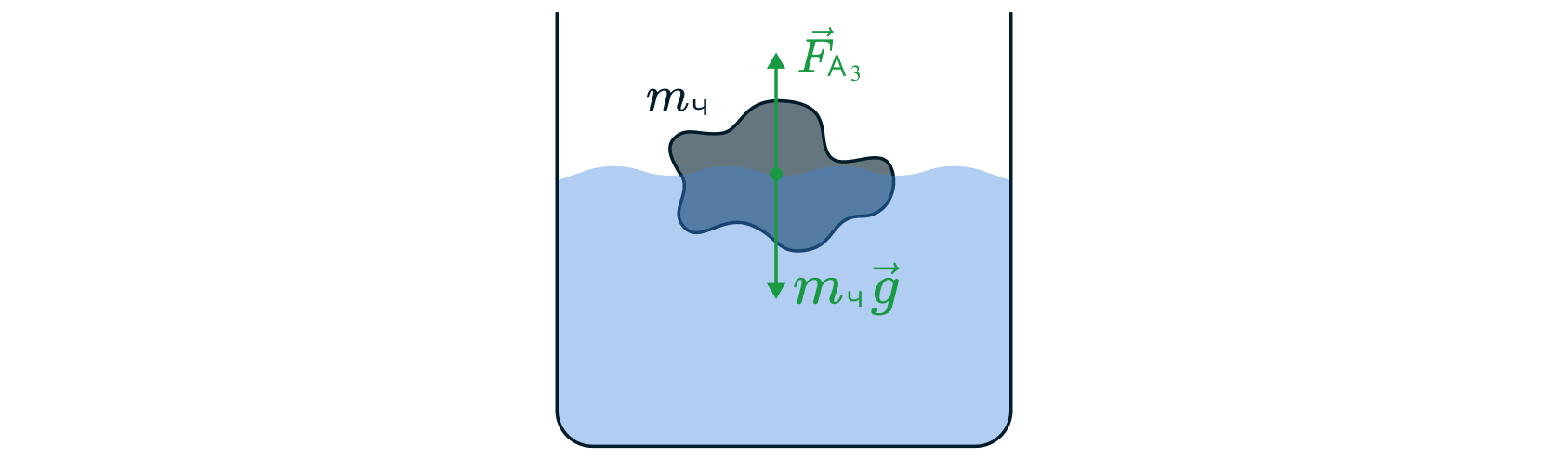
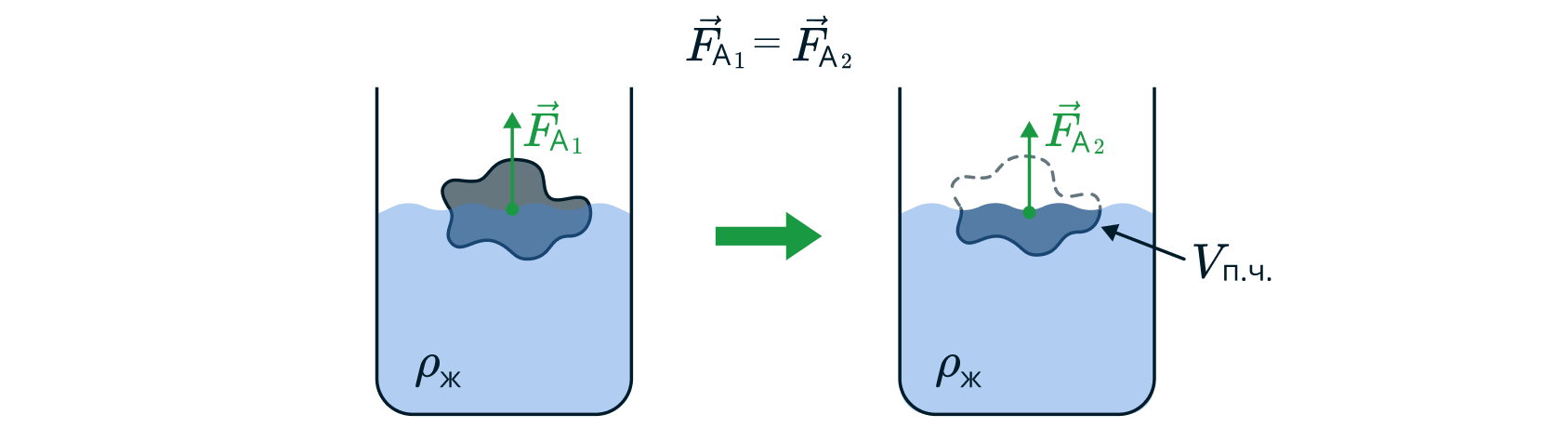
Уберем мысленно часть тела, не погруженную в воду — на нее не действуют никакие выталкивающие силы, от такого действия сила Архимеда не изменится. Но теперь мы получили тело, погруженное в жидкость целиком, объем которого равен объему погруженной части деревянного тела. Отсюда вывод: сила Архимеда, действующая на тело, равна весу жидкости в объеме погруженной части (или в объеме вытесненной телом части) $FАрх = ρжgVп.ч.$ .

$PIC$

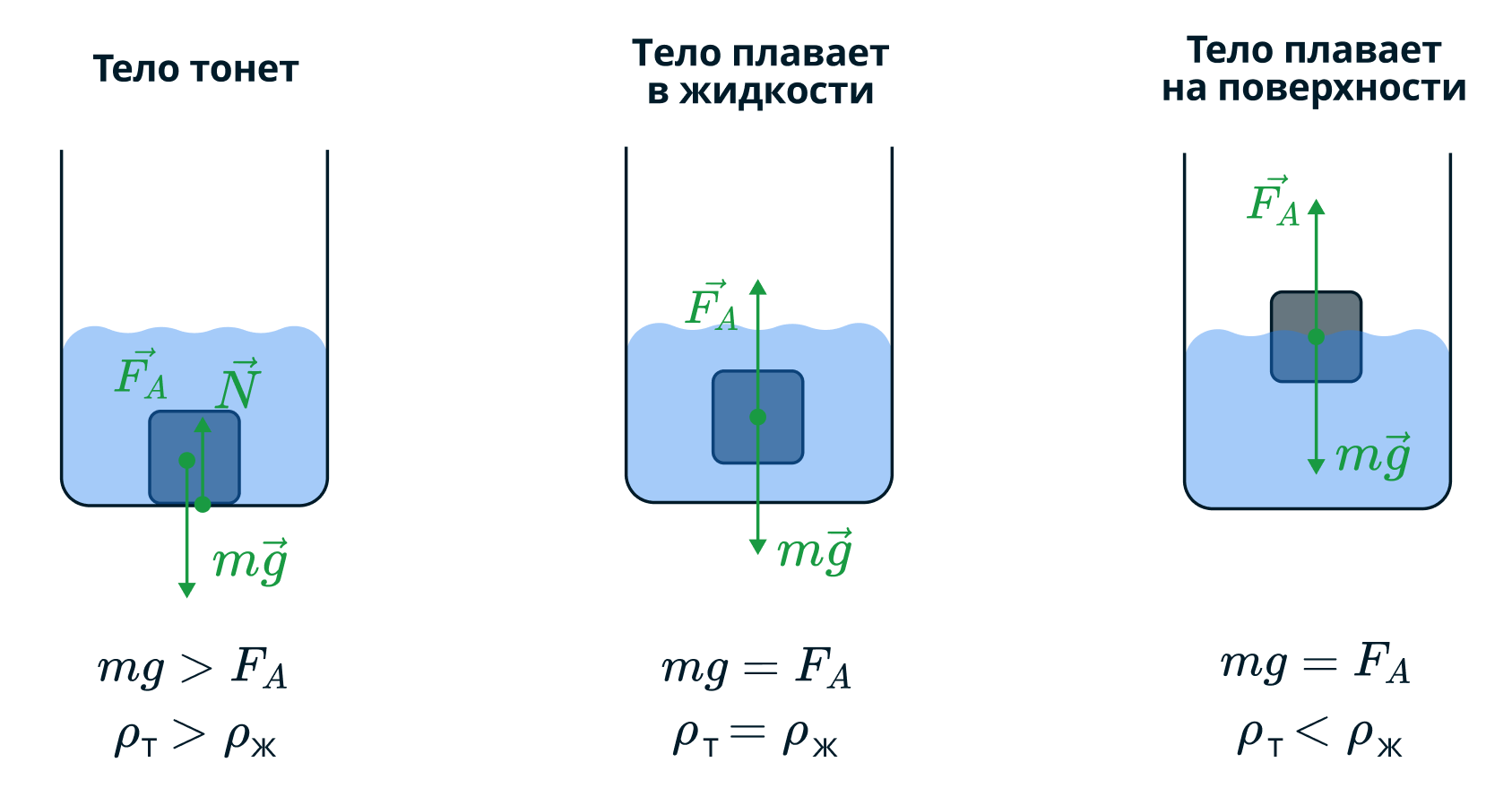
Условия плавания тел

Рассмотрим тело плотностью $ρт$ и объемом $V$ . Пусть тело полностью погрузили в жидкость плотностью $ρж$ и отпустили. Тогда на тело в момент погружения действуют сила тяжести $Fтяж = ρтV g$ и сила Архимеда $FАрх = ρжV g$ . С этого момента существуют три варианта развития событий:

Если сила тяжести больше силы Архимеда $mg > FА$ , или $ρт > ρж$ , тело начинает тонуть.
Если сила тяжести равна силе Архимеда $mg = FА$ , или $ρт = ρж$ , тело остается неподвижным в состоянии равновесия.
Если сила тяжести меньше силы Архимеда $mg < FА$ , или $ρт < ρж$ , тело всплывает до поверхности жидкости. Далее объем погруженной части тела начинает уменьшаться и, соответственно, уменьшается сила Архимеда (при том, что сила тяжести остается постоянной). В некоторый момент силы сравняются, тело продолжит всплывать по инерции, сила тяжести перевесит силу Архимеда, и тело начнет движение вниз. Возникают затухающие колебания, после которых тело установится в положении, соответствующем равенству сил $F Арх = mg$ .

$PIC$

Предыдущая справка

Следующая справка