Метод площадей для решения задач

▶▸ Теорема 1. Если вершину треугольника перемещать по прямой, параллельной противолежащей стороне, то площадь при этом останется прежней.

 

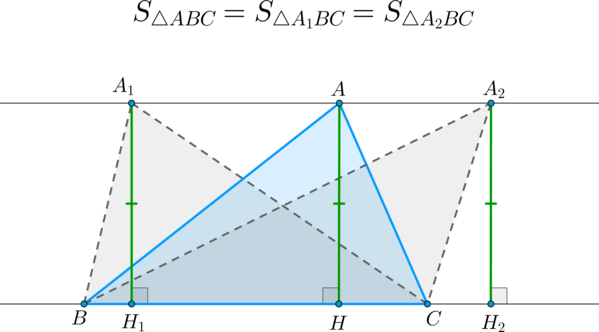
Доказательство: Рассмотрим три треугольника △ABC,△A1BC,△A2BC△ABC,△A1BC,△A2BC. Т.к. A1A2∥BCA1A2∥BC, то расстояние от любой точки одной из этих прямых до другой прямой одинаково. То есть высоты, опущенные из точек A,A1,A2A,A1,A2 на прямую BCBC будут равны: AH=A1H1=A2H2=hAH=A1H1=A2H2=h. Т.к. у этих треугольников общее основание BCBC, то: S△ABC=S△A1BC=S△A2BC=12BC⋅hS△ABC=S△A1BC=S△A2BC=12BC⋅h

 

▶▸ Теорема 2. Если два треугольника имеют равные высоты (общую высоту), то их площади относятся как основания, к которым эти высоты проведены.

 

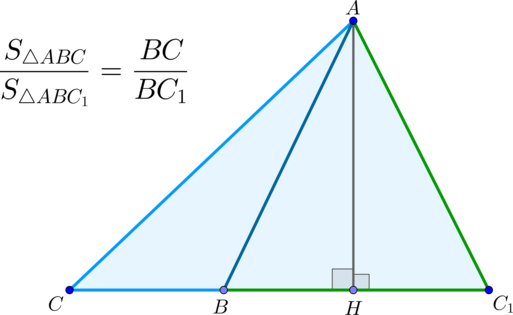
Доказательство: Рассмотрим треугольники △ABC△ABC и △ABC1△ABC1: т.к. высота треугольника — это перпендикуляр, опущенный из вершины на прямую, содержащую противолежащую сторону, то AHAH — высота и △ABC△ABC, и △ABC1△ABC1. Следовательно: S△ABCS△ABC1=12AH⋅BC12AH⋅BC1=BCBC1S△ABCS△ABC1=12AH⋅BC12AH⋅BC1=BCBC1

 

▶▸ Теорема 3. Если два треугольника имеют одинаковые стороны (общую сторону), то их площади относятся как высоты, которые к этим сторонам проведены.

 

Доказательство: Рассмотрим треугольники △ABC△ABC и △ABC1△ABC1. Проведем на их общую сторону ABAB высоты CHCH и C1H1C1H1. Тогда: S△ABCS△ABC1=12CH⋅AB12C1H1⋅AB=CHC1H1S△ABCS△ABC1=12CH⋅AB12C1H1⋅AB=CHC1H1

 

▶▸ Следствие: Медиана треугольника делит его на два треугольника, равных по площади.

 

Доказательство: по теореме 2 площади △ABM△ABM и △CBM△CBM относятся как основания AMAM и CMCM. Но AM=CM⇒S△ABM=S△CBMAM=CM⇒S△ABM=S△CBM.

 

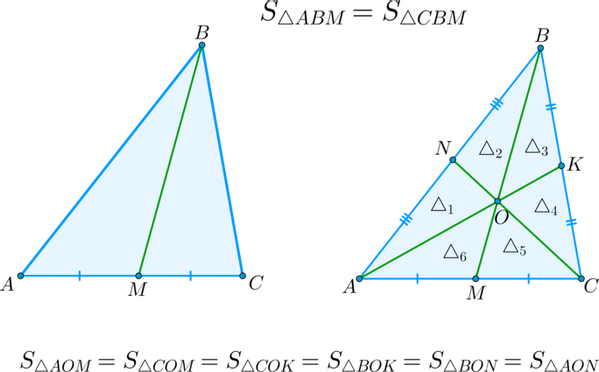
▶▸ Следствие: Все три медианы треугольника делят его на шесть треугольников, равных по площади.

 

Доказательство: т.к. AKAK — медиана △ABC△ABC, то S△1+S△2+S△3=S△4+S△5+S△6S△1+S△2+S△3=S△4+S△5+S△6.

 

Т.к. OKOK — медиана △OBC△OBC, то S△3=S△4S△3=S△4. Следовательно, S△1+S△2=S△5+S△6 (∗)S△1+S△2=S△5+S△6 (∗).

 

Т.к. ONON — медиана △AOB△AOB, то S△1=S△2S△1=S△2, аналогично, S△5=S△6S△5=S△6. Следовательно, подставляя эти равенства в (∗)(∗), получим: 2S△1=2S△6⇒S△1=S△6⇒S△2=S△52S△1=2S△6⇒S△1=S△6⇒S△2=S△5.

 

Аналогично доказывается, что S△4=S△5S△4=S△5. Таким образом, площади всех этих треугольников равны.

 

▶▸ Теорема 4. Если два треугольника имеют по равному углу (общему углу), то их площади относятся как произведения сторон, образующих эти углы.

 

Доказательство: Рассмотрим треугольники △B1AC1△B1AC1 и △BAC△BAC, имеющие равный (общий) ∠A∠A. Т.к. площадь треугольника равна полупроизведению сторон на синус угла между ними, то: S△BACS△B1AC1=12sin∠A⋅BA⋅AC12sin∠A⋅B1A⋅AC1=BA⋅ACB1A⋅AC1S△BACS△B1AC1=12sin⁡∠A⋅BA⋅AC12sin⁡∠A⋅B1A⋅AC1=BA⋅ACB1A⋅AC1

 

▶▸ Следствие: Биссектриса угла треугольника делит его на два треугольника, площади которых относятся как стороны, образующие этот угол.

 

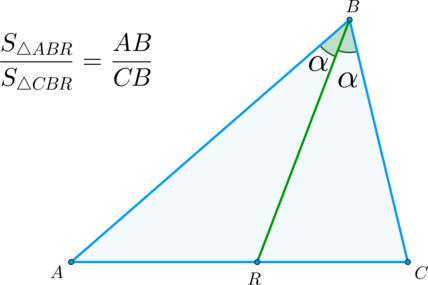
Доказательство: S△ABRS△CBR=12sinα⋅AB⋅BR12sinα⋅CB⋅BR=ABCBS△ABRS△CBR=12sin⁡α⋅AB⋅BR12sin⁡α⋅CB⋅BR=ABCB

 

▶▸ Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

 

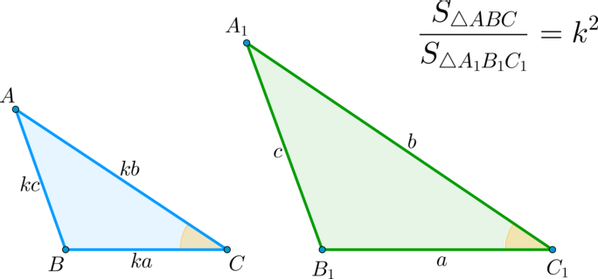
Доказательство: т.к. треугольники подобны, то все стороны одного треугольника в kk раз больше всех сторон другого, а углы между сходственными сторонами равны. Значит, S△ABCS△A1B1C1=12sin∠C⋅BC⋅AC12sin∠C1⋅B1C1⋅A1C1=ka⋅kba⋅b=k2S△ABCS△A1B1C1=12sin⁡∠C⋅BC⋅AC12sin⁡∠C1⋅B1C1⋅A1C1=ka⋅kba⋅b=k2

 

▶▸ Следствие: Все три средние линии треугольника делят его на четыре равных треугольника, и, как следствие, равных по площади.

 

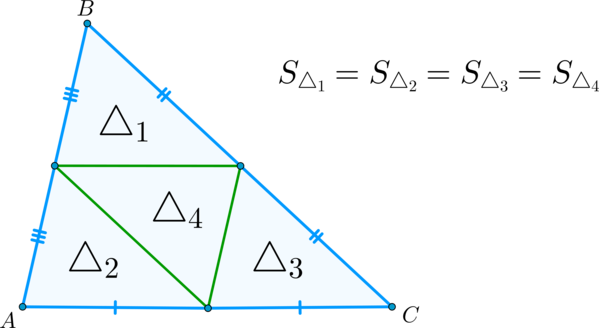
Доказательство: △1,△2,△3∼△ABC△1,△2,△3∼△ABC с коэффициентом подобия 1212. Следовательно, S△1=S△2=S△3=14S△ABC⇒S△4=S△ABC−3S△1=14S△ABCS△1=S△2=S△3=14S△ABC⇒S△4=S△ABC−3S△1=14S△ABC