Теорема синусов и теорема косинусов

Теорема синусов

В любом треугольнике отношение стороны к синусу противолежащего угла не зависит от выбора стороны и равно диаметру описанной окружности.

 

Доказательство

 

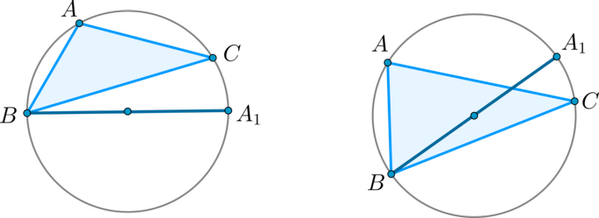
Пусть $R$ – радиус окружности, описанной около треугольника $ABC$. Проведём диаметр $BA_1$ и рассмотрим треугольник $A_1BC$ (случай, когда точки $A_1$ и $C$ совпадают, рассмотрите самостоятельно). Угол $C$ этого треугольника прямой, поэтому $BC = BA_1\cdot \sin\angle A_1$, но $\sin\angle A = \sin\angle A_1$ так как углы $A$ и $A_1$ либо отличаются на угол, равный $180^\circ$, либо совпадают.

 

Следовательно, $BC = BA_1\cdot\sin\angle A$, то есть $\dfrac{BC}{\sin\angle A} = 2R$. Так как в доказательстве мы не ограничивали общности, то равенства $\dfrac{AC}{\sin\angle B} = 2R = \dfrac{AB}{\sin\angle C}$ показываются аналогично.

 

Теорема косинусов

В любом треугольнике квадрат стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

 

Доказательство

Пусть в треугольнике $ABC$ $AB = c$, $AC = b$, $BC = a$, $\angle C=\alpha$. Докажем, что $c^2=a^2+b^2-2ab\cdot\cos\alpha$.

 

Проведем высоту $BH=h$. Пусть она разбила сторону $AC$ на отрезки длиной $x$ и $y$:

 

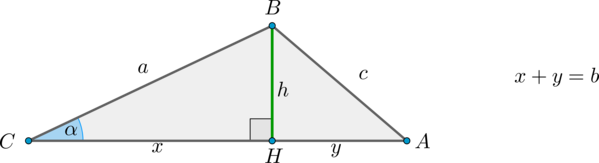
По теореме Пифагора из $\triangle AHB: \ c^2=h^2+y^2$;
из $\triangle CHB: \ a^2=x^2+h^2$.

Вычтем из первого равенства второе: $c^2-a^2=y^2-x^2 \Rightarrow c^2=a^2+(y-x)(y+x)=a^2+b(y-x)$.

Заметим, что $\cos\alpha=\dfrac xa \Rightarrow x=a\cos\alpha$. Тогда:

$$c^2=a^2+b(y+x-2x)=a^2+b(b-2x)=a^2+b(b-2a\cos\alpha)=a^2+b^2-2ab\cos\alpha$$

Замечание

С помощью данных теорем можно легко найти все элементы треугольника, если известны, например, две стороны и угол, угол и две стороны, три стороны и т.д.

 

Пример

Найти стороны и углы треугольника, если медиана $BM$, проведенная к стороне $AC=4$, равна $2\sqrt3$, а угол треугольника $\angle A=60^\circ$.

 

Решение. Рассмотрим данный треугольник:

 

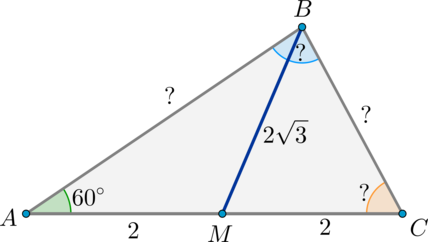
1) По теореме косинусов из $\triangle ABM$:
$(2\sqrt3)^2=2^2+AB^2-2\cdot 2\cdot AB\cdot \cos60^\circ \Rightarrow AB^2-2AB-8=0 \Rightarrow AB=4$

 

2) $\triangle ABC$ – равнобедренный ($AB=AC=4$), следовательно, $\angle B=\angle C=\frac12\left(180^\circ-\angle A\right)=60^\circ$.

 

Значит, $\triangle ABC$ – правильный, значит, $BC=4$.