Векторы
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#884
Понятие вектора
Рассмотрим произвольный отрезок На нём можно указать два направления: от
к
и наоборот.

Чтобы выбрать одно из этих направлений, одну из точек и
назовём началом отрезка, а вторую — концом отрезка и будем
считать, что отрезок направлен от начала к концу.
Определение: Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется направленным отрезком, или вектором.
На рисунках вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают двумя
заглавными латинскими буквами со стрелкой над ними, например Первая буква обозначает начало вектора,
вторая — его конец. Векторы часто обозначают и одной строчной латинской буквой со стрелкой над ней, например
Любая точка плоскости также является вектором. В этом случае вектор называется нулевым. Начало нулевого вектора совпадает
с его концом. Нулевой вектор обозначается символом
Длиной, или модулем ненулевого вектора называется длина отрезка
Длина вектора
обозначается так:
Длина нулевого вектора считается равной нулю:
Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Пусть две пунктирные прямые параллельны. Тогда
и
коллинеарны, а вот
не коллинеарен ни одному из них, так
как он не находится ни на одной из пунктирных прямых, ни на прямой, параллельной им.
Коллинеарные векторы можно разбить на две группы: сонаправленные и противоположно направленные векторы.
В нашем примере сонаправленными являются векторы
и
векторы
и
являются противоположно
направленными; векторы
и
являются противоположно направленными; векторы
и
являются противоположно
направленными.
Нулевой вектор считается колинеарным и сонаправленным любому вектору.
Равенство векторов
Определение: Векторы называются равными, если они сонаправлены и их длины равны.
На самом деле вектор — это сдвиг точки
в точку
Тогда этот вектор двигает не только точку
но и всю
плоскость.
Векторы равны, если они сонаправлены и их длины равны, поэтому не важно, где находится наш вектор. Мы можем отложить от
разных точек направленный отрезок но с точки зрения векторов это будет один и тот же вектор. Получается, что вектор это не
только конкретный направленный отрезок, на самом деле это целый класс всех равных направленных отрезков, которые
одинаково двигают плоскость. Таким образом, в задачах любой вектор мы можем рисовать где угодно в удобном для нас
месте.
Сложение векторов
Пусть точка переместилась из положения в положение
а затем из положения
в положение
В результате этих
двух перемещений, которые можно представить векторами
и
точка переместилась из положения
в положение
Поэтому результат перемещения можно представить как вектор
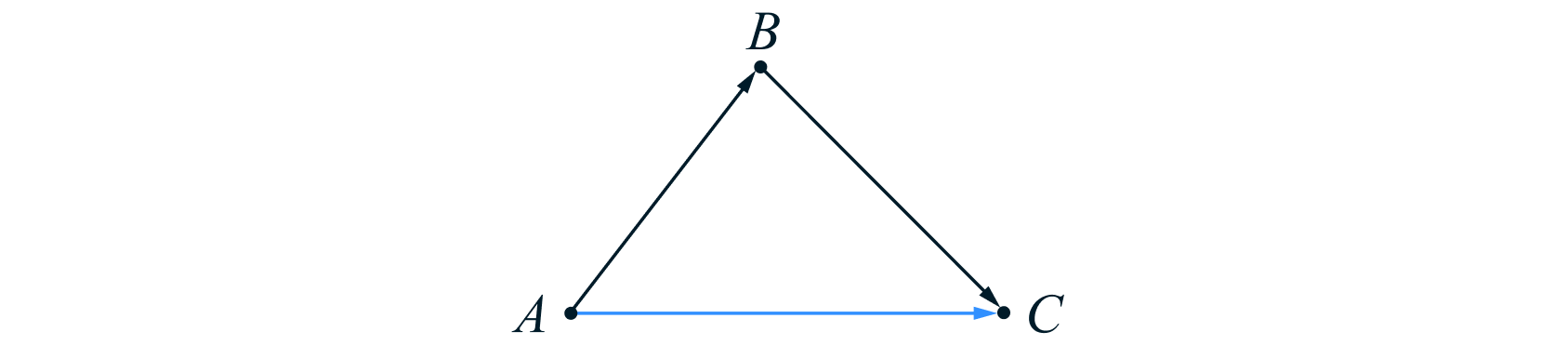
Поскольку перемещение из в
складывается из перемещения из
в
и перемещения из
в
то
Правило треугольника
Пусть и
— два вектора, которые мы хотим сложить. Обозначим начало вектора
за точку
его конец за точку
и
параллельно перенесем начало вектора
в точку
Пусть получился вектор
равный
Тогда вектор
называется суммой векторов
и
Такое правило сложения векторов называется правилом треугольника.
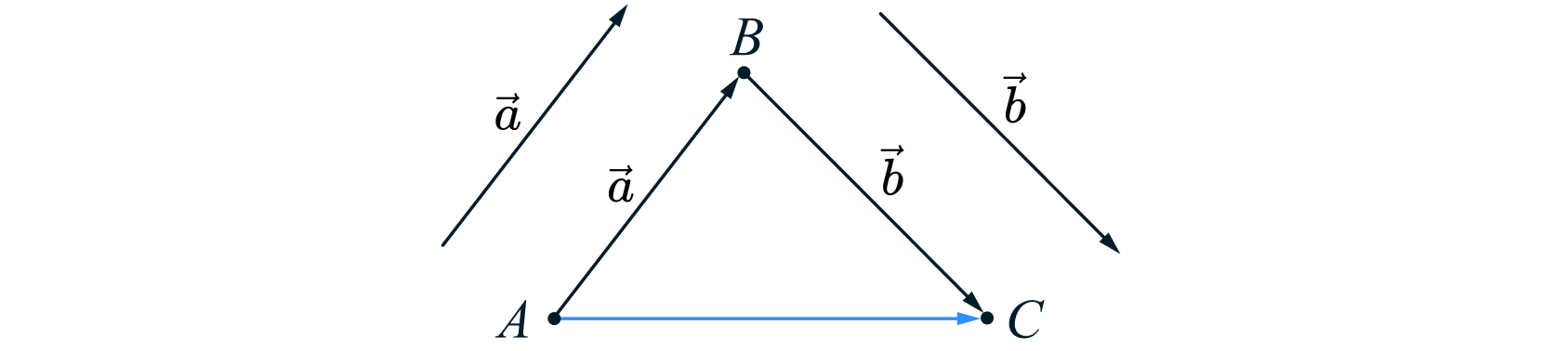
Правило параллелограмма
Рассмотрим случай, когда векторы и
выходят из одной точки. В таком случае мы можем достроить эту конструкцию до
параллелограмма и получить из каждой пары противоположных сторон пары равных векторов.
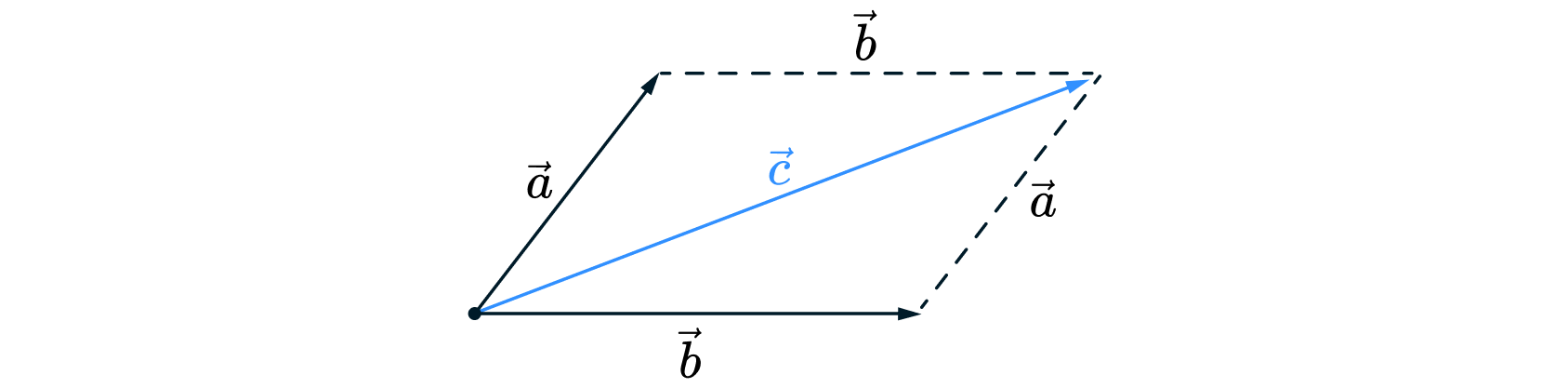
Тогда по правилу треугольника
Вычитание векторов
Для начала поймем, что «» перед вектором просто меняет его направление. Таким образом, векторы
и
равны по
длине, коллинеарны и противоположно направлены.
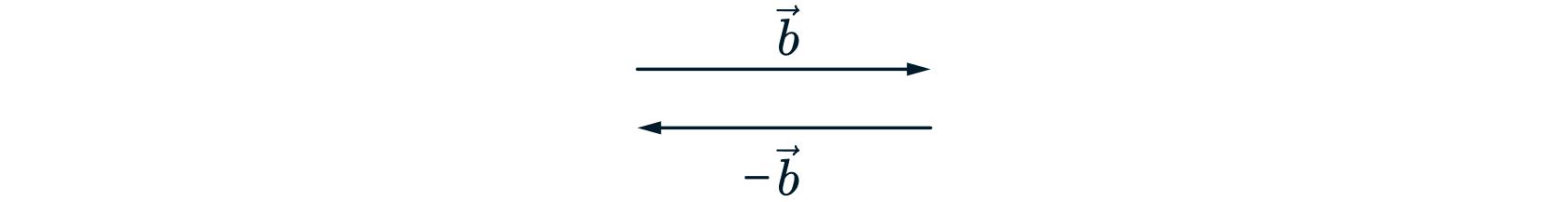
Пусть есть векторы и
отложенные из одной точки. Пусть при этом вектор
такой, что
то есть вектор
можно получить, сложив векторы
и
по правилу треугольника.
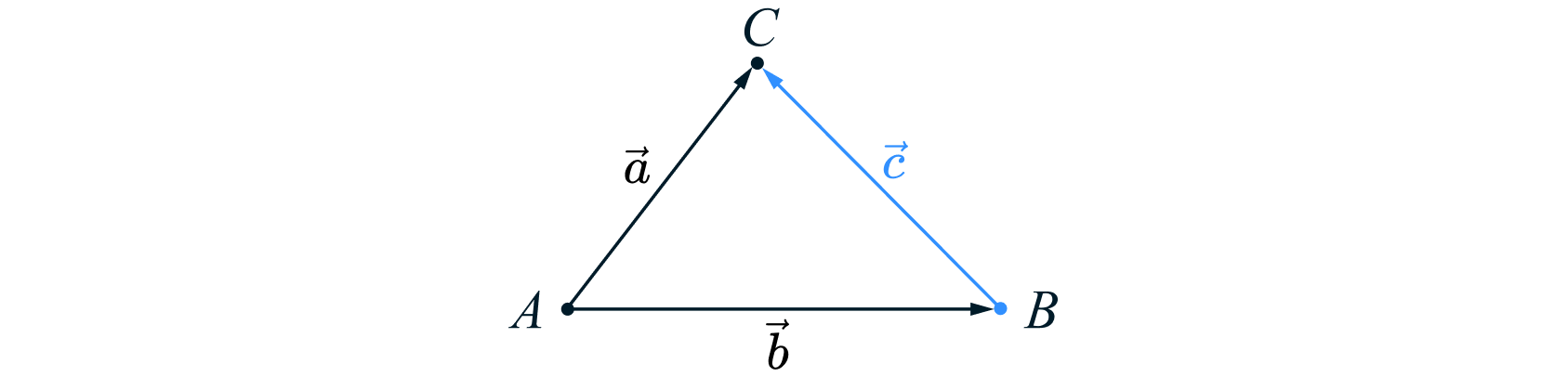
Тогда обозначим и назовем вектор
разностью векторов
и
Разность векторов можно определить и по-другому. При тех же исходных условиях заменим вектор на вектор
Тогда
разностью векторов
и
назовем вектор
равный
Таким образом, можем изобразить вектор
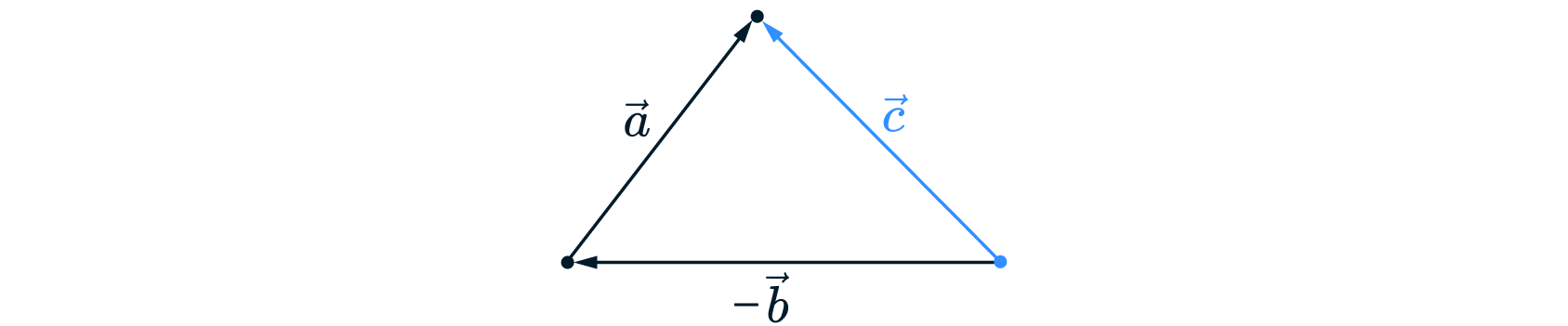
Как мы видим, вектор получается один и тот же независимо от способа определения. Следовательно, на практике можем
искать разность двух векторов тем способом, который в условиях конкретной задачи кажется более удобным.
Умножение вектора на число
Возьмем вектор Попробуем найти вектор
Тогда переместить точку на вектор
— это то же самое, что и дважды
переместить её на вектор
Также можем разделить вектор на два равных вектора и получить вектор
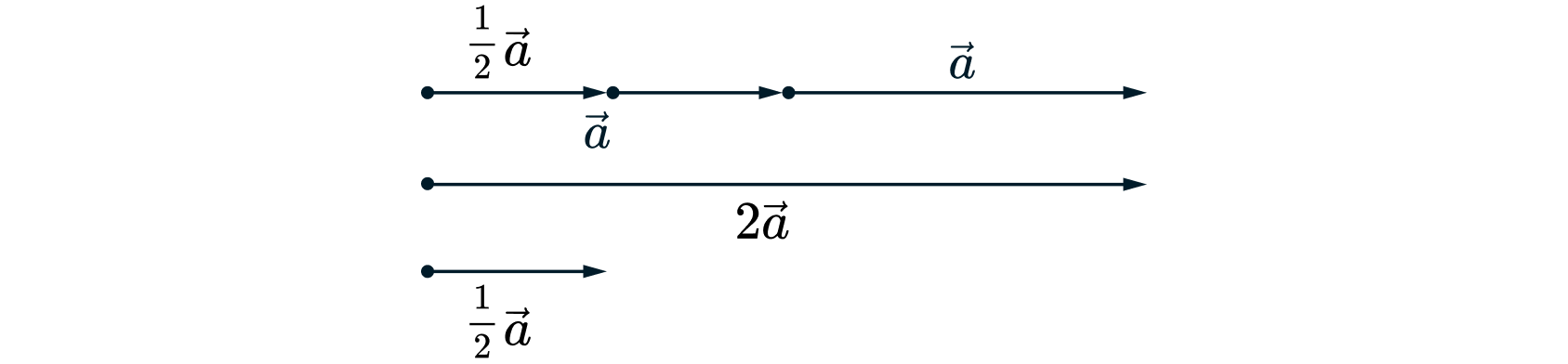
Правила умножения вектора на число
Пусть и
— некоторые числа,
и
— некоторые векторы. Тогда
