Математика в физике

Линейная функция

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Математика в физике

Теоретическая справка

#885

Линейная функция

Линейной функцией называется функция вида $y = kx+ b,$ где $k$ и $b$ — постоянные действительные коэффициенты. Графиком линейной функции является прямая.

Число $k$ называется угловым коэффициентом прямой.

Число $b$ называется свободным членом и равно ординате точки пересечения графика прямой с осью $Oy,$ так как при $x= 0,$ $y = k⋅0+ b= b.$

Рассмотрим, как выглядят графики линейных функций в зависимости от значений коэффициентов $k$ и $b.$

При $k = 0$ получаем функцию $y = b.$ При любом значении $x$ функция принимает значение равное $b,$ то есть множество значений функции состоит из единственного числа $b.$ Тогда графиком этой функции является прямая, параллельная оси абсцисс. Заметим, что при $b= 0$ график функции $y =b$ совпадает с осью $Ox.$

$PIC$
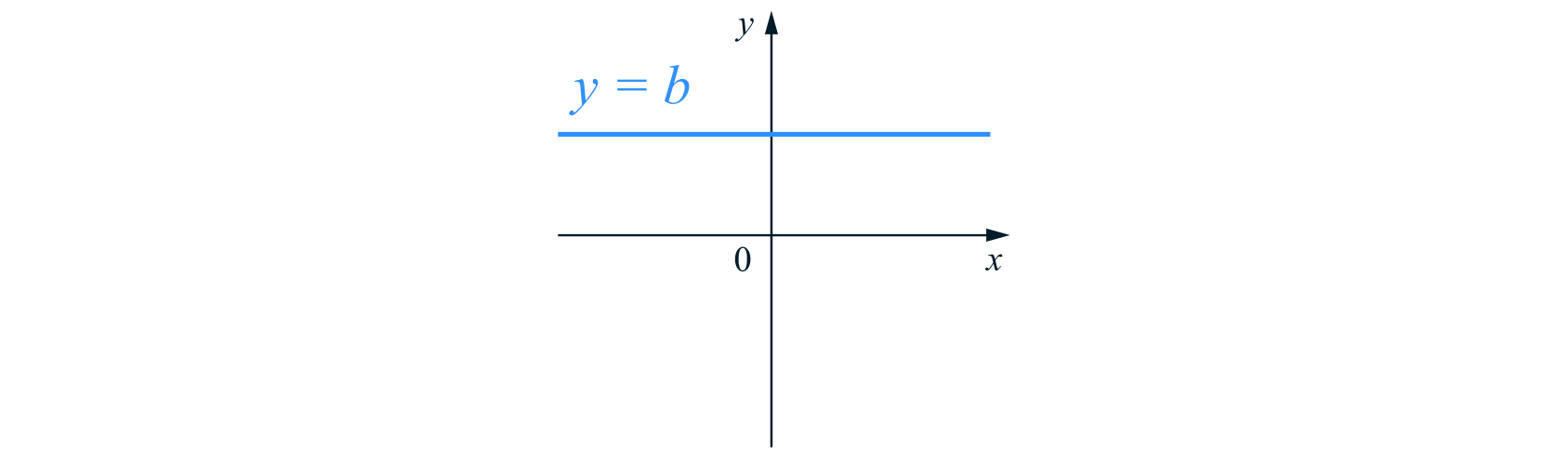
При $k ⁄= 0,$ $b= 0$ получаем функцию $y = kx.$ Заметим, что при $x = 0,$ $y = k⋅0 =0.$ Тогда график функции — прямая, проходящая через начало координат.

$PIC$
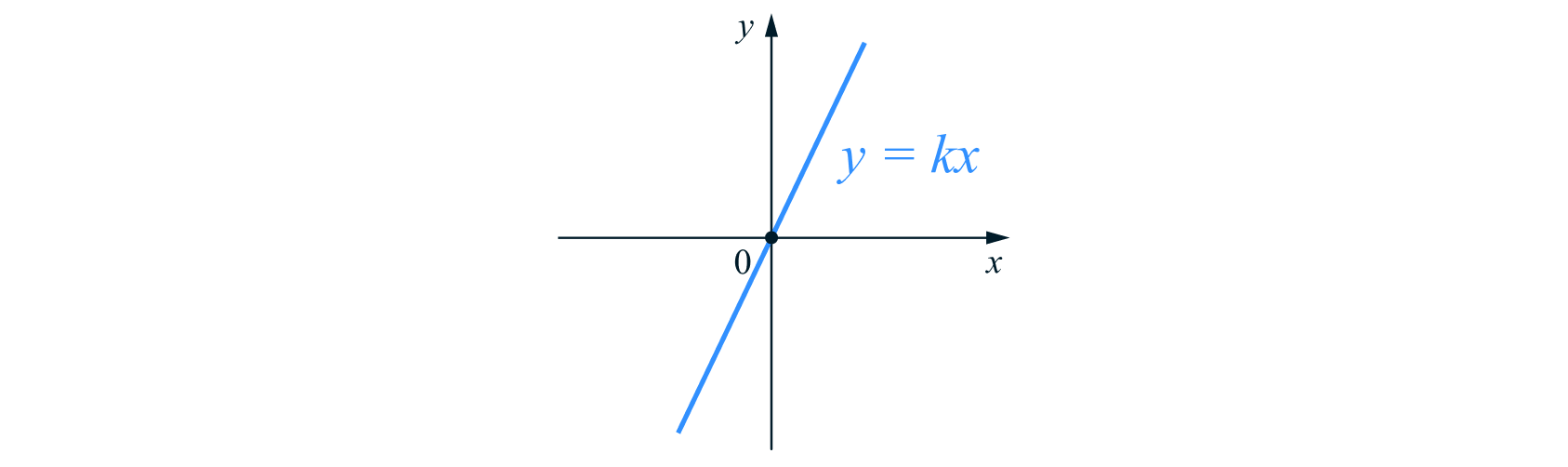
При $k ⁄= 0,$ $b⁄= 0$ получаем функцию $y = kx +b.$ Найдем точки пересечения прямой с осями координат:
Чтобы найти точку пересечения графика функции с осью $Oy,$ нужно найти значение функции в точке ноль
$y(0)= k⋅0 +b =b$
То есть прямая пересекает ось ординат в точке $B(0;b).$
Чтобы найти точки пересечения графика функции с осью $Ox,$ нужно найти, при каких значениях аргумента $y(x)= 0,$ то есть решить уравнение $kx+ b= 0.$ Получаем $x= − bk.$
Таким образом, прямая пересекает ось абсцисс в точке $b A(− k;0).$

$PIC$
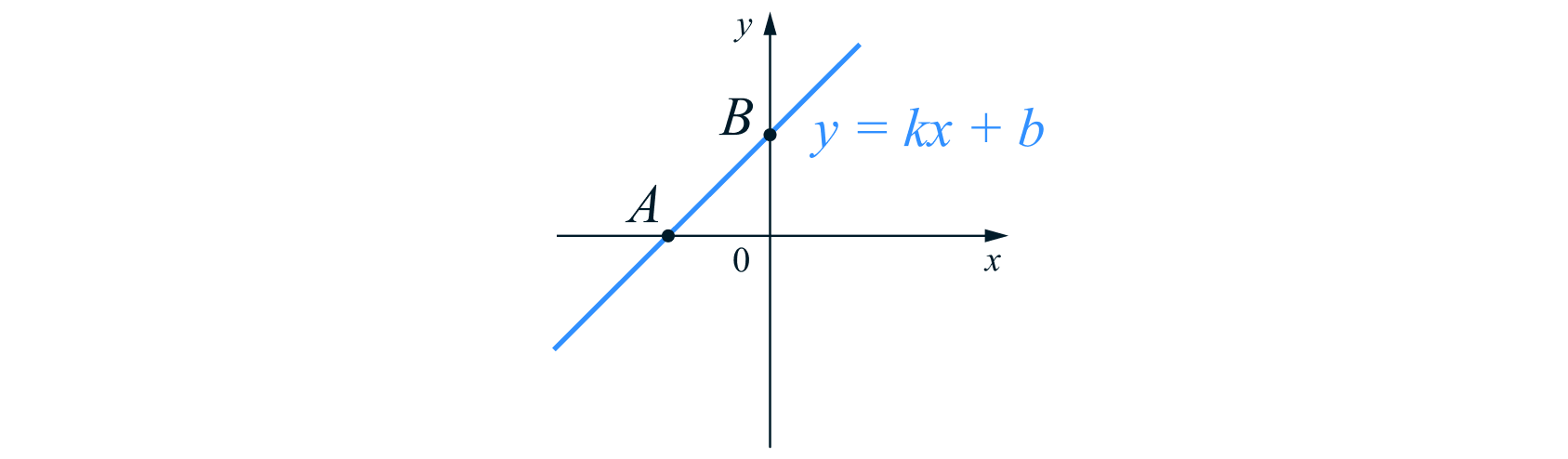
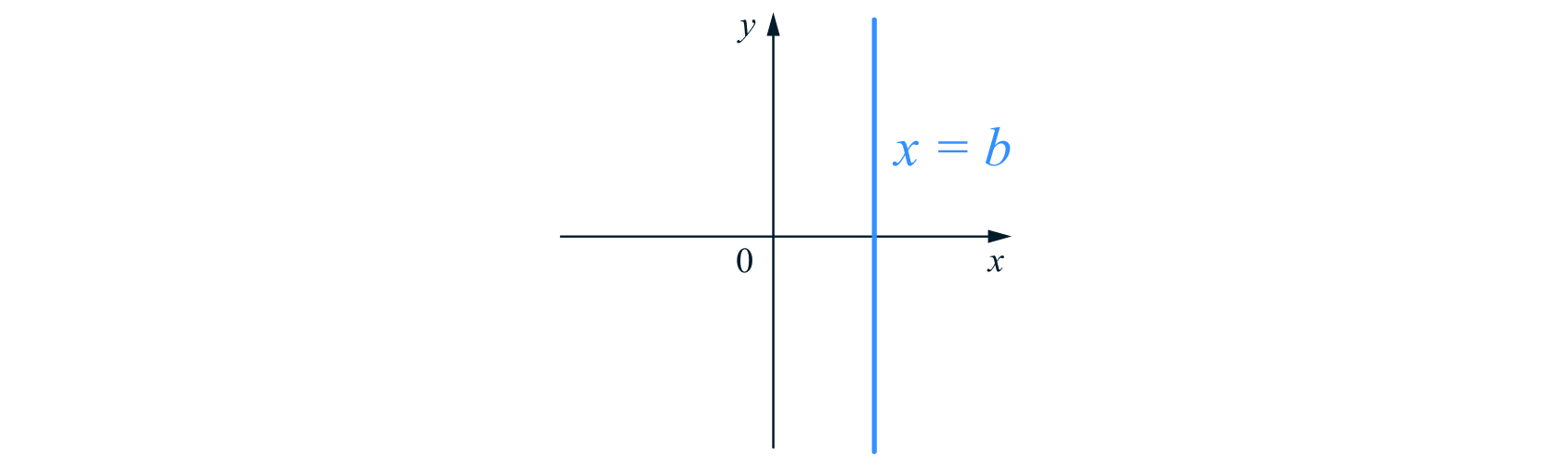
В предыдущих пунктах мы описали все прямые, кроме вертикальных. Они задаются уравнением $x = b.$ При $b = 0$ график уравнения $x= b$ совпадает с осью $Oy.$

$PIC$

Рассмотрим, как коэффициент $k$ влияет на прямую:

Если $k > 0,$ то при $x1 > x2,$ получаем $kx1 > kx2$ и $kx1+ b> kx2+ b,$ то есть при увеличении аргумента значение функции увеличивается, а значит прямая возрастает.
Если $k < 0,$ то при $x1 > x2,$ получаем $kx1 < kx2$ и $kx1+ b< kx2+ b,$ то есть при увеличении аргумента значение функции уменьшается, а значит прямая убывает.

Посмотрим, как выглядят графики линейных функций при различных значениях $k$ и $b.$

$PIC$

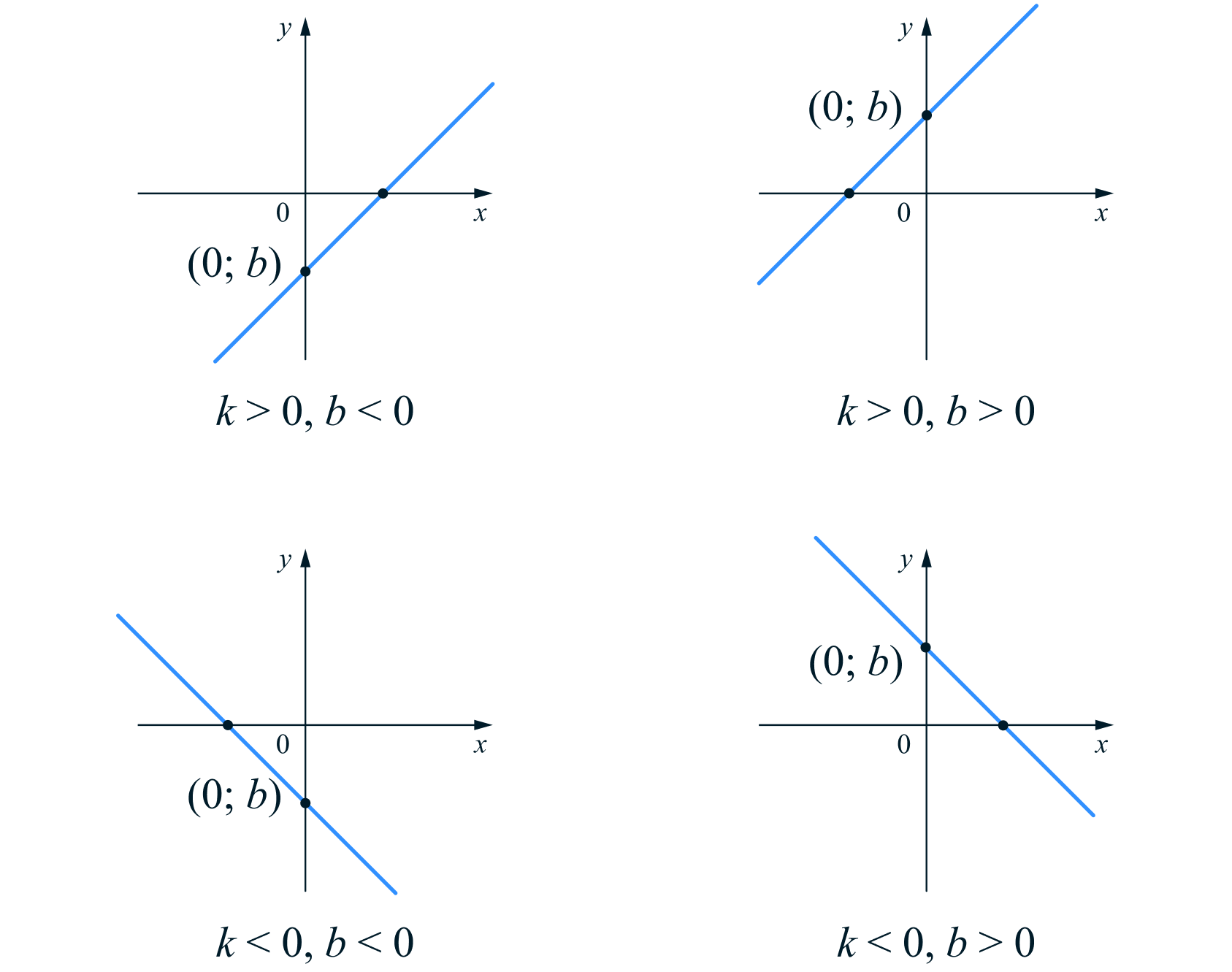
Для $y = kx+ b$ угловой коэффициент $k$ равен тангенсу угла наклона прямой к положительному направлению оси $Ox$ (сокращенно будем говорить «угол наклона»).

$PIC$

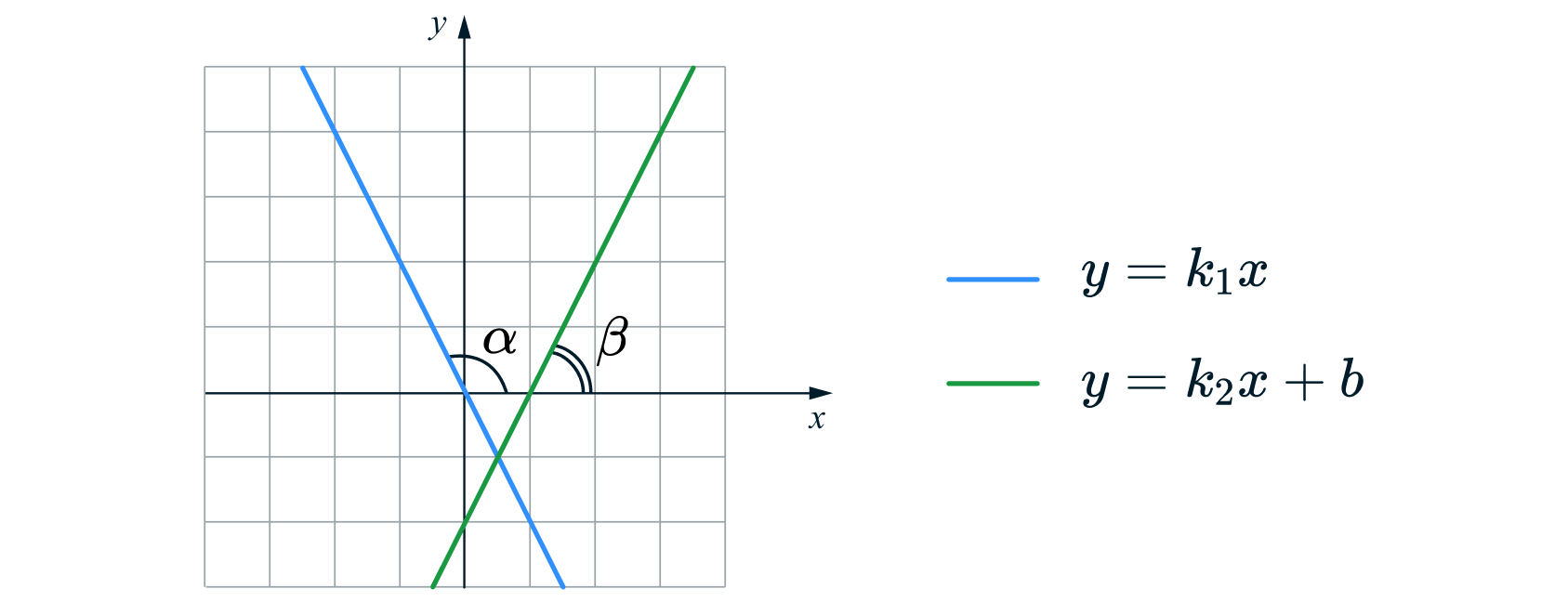
Так, на картинке выше $k1 = tgα,$ $k2 = tgβ.$

На этом моменте еще раз можем отметить, что при $k > 0$ прямая возрастает, так как коэффициент $k$ равен тангенсу угла наклона прямой, а если тангенс угла положительный, то угол наклона острый. Аналогично, если $k < 0,$ то тангенс угла наклона отрицательный, откуда получаем что угол наклона тупой и прямая убывает.

Свойства линейной функции

Перечислим свойства линейной функции $f(x) =kx + b$ при $k ⁄= 0.$

Область определения функции— множество всех действительных чисел. $D(f)= R.$
Множество значений функции— множество всех действительных чисел. $E(f)= R.$
Функция не ограничена и не имеет ни наибольшего, ни наименьшего значений.
При $b= 0$ функция $y = kx$ является нечетной. Тогда её график симметричен относительно начала координат.
При $b⁄= 0$ функция не является ни четной, ни нечетной.
Функция непериодическая.
График функции пересекает ось $Oy$ в точке $(0;b),$ ось $Ox$ в точке $-b (−k ;0).$
$x= − b k$ является нулем функции.
При $k > 0$ функция принимает положительные значения на промежутке $(− b ;+ ∞), k$ отрицательные — на промежутке $b (− ∞;− k).$
При $k < 0$ функция принимает положительные значения на промежутке $(−∞; − bk),$ отрицательные — на промежутке $(− b;+∞ ). k$
При $k > 0$ функция возрастает на всей области определения.
При $k < 0$ функция убывает на всей области определения.

Предыдущая справка

Следующая справка