Математика в физике

Квадратичная функция

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Математика в физике

Теоретическая справка

#886

Квадратичная функция

Квадратичной функцией называется функция вида $2 y = ax + bx+ c,$ где $a,b$ и $c$ — постоянные действительные коэффициенты, причем $a⁄= 0.$ Графиком квадратичной функции является парабола.

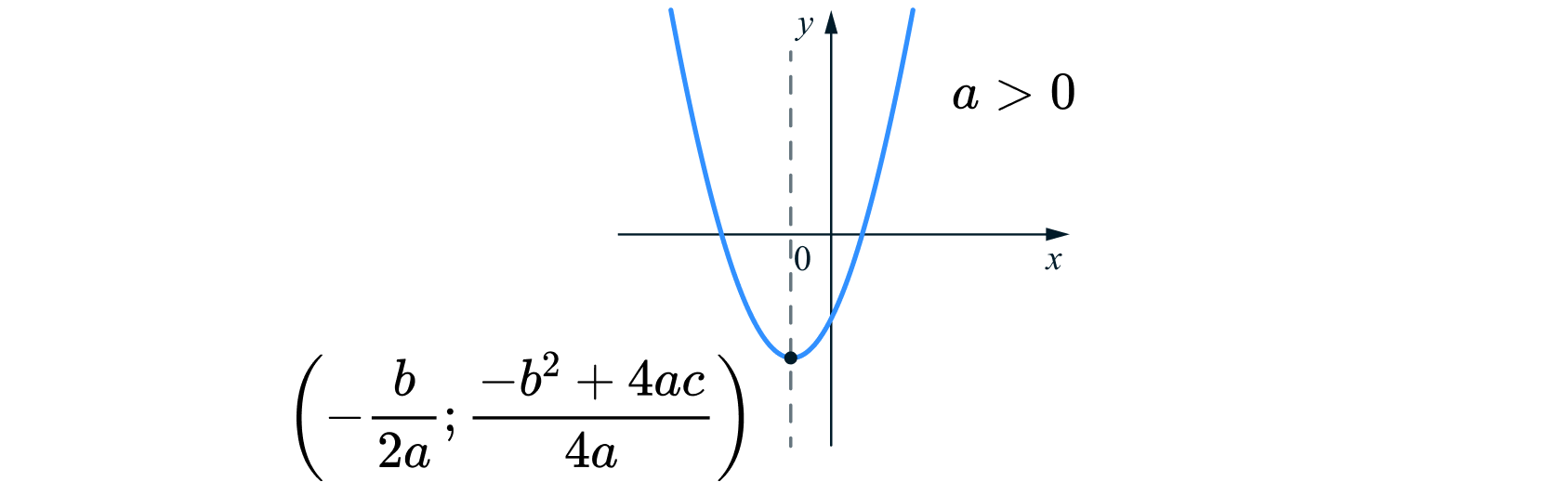
Координаты вершины параболы

Рассмотрим функцию $y = ax2+bx +c.$ Выделим полный квадрат:

b c b b b c b b2 c b − b2+ 4ac b −b2+ 4ac ax2+ bx + c= a(x2+ a x+ a)= a(x2+ 2⋅2a ⋅x + (2a )2− (2a)2+ a)== a((x+ 2a)2− 4a2 + a )= a((x+ 2a)2+---4a2---)= a(x+ 2a)2+ ---4a---

При $a> 0$ функция принимает наименьшее значение в точке $x = − b-, 0 2a$ при $a < 0$ функция принимает наибольшее значение в точке $x0 =− -b, 2a$ тогда $x0$ — абсцисса вершины параболы. Чтобы найти ординату вершины параболы, нужно найти значение функции в точке $x0,$ получаем $−b2+ 4ac y0 =---4a---.$

Таким образом, вершина параболы находится в точке $2 (− b-; −-b-+-4ac). 2a 4a$

Кроме того, если $a > 0,$ то при удалении аргумента $x$ от $x0,$ значение функции будет увеличиваться, то есть ветви параболы будут направлены вверх.

$PIC$

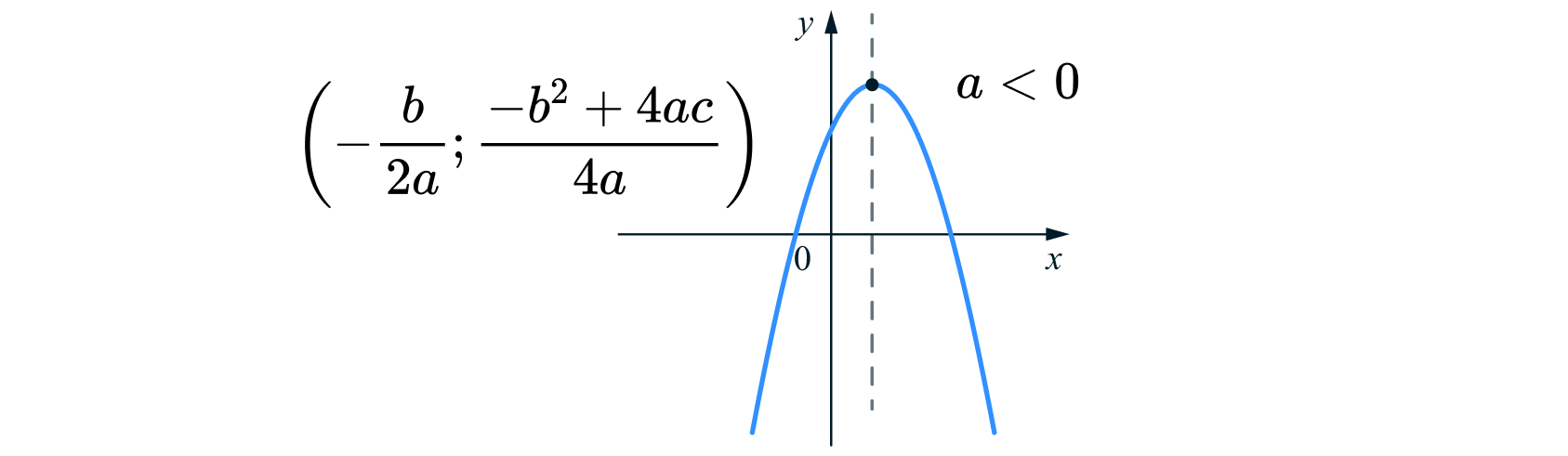
Если $a < 0,$ то при удалении аргумента $x$ от $x0,$ значение функции будет уменьшаться, то есть ветви параболы будут направлены вниз.

$PIC$

Также понимаем, что прямая $x= − b- 2a$ — ось симметрии параболы.

Пересечение параболы с осями координат

Чтобы найти точку пересечения графика функции $y = ax2+ bx+ c$ с осью $Oy,$ найдем значение функции в точке ноль:

y(0)= a⋅02+ b⋅0+ c= c

Таким образом, парабола пересекает ось $Oy$ в точке $(0;c).$

Посмотрим, как выглядят графики квадратичных функций при различных значениях $a$ и $c.$

$PIC$

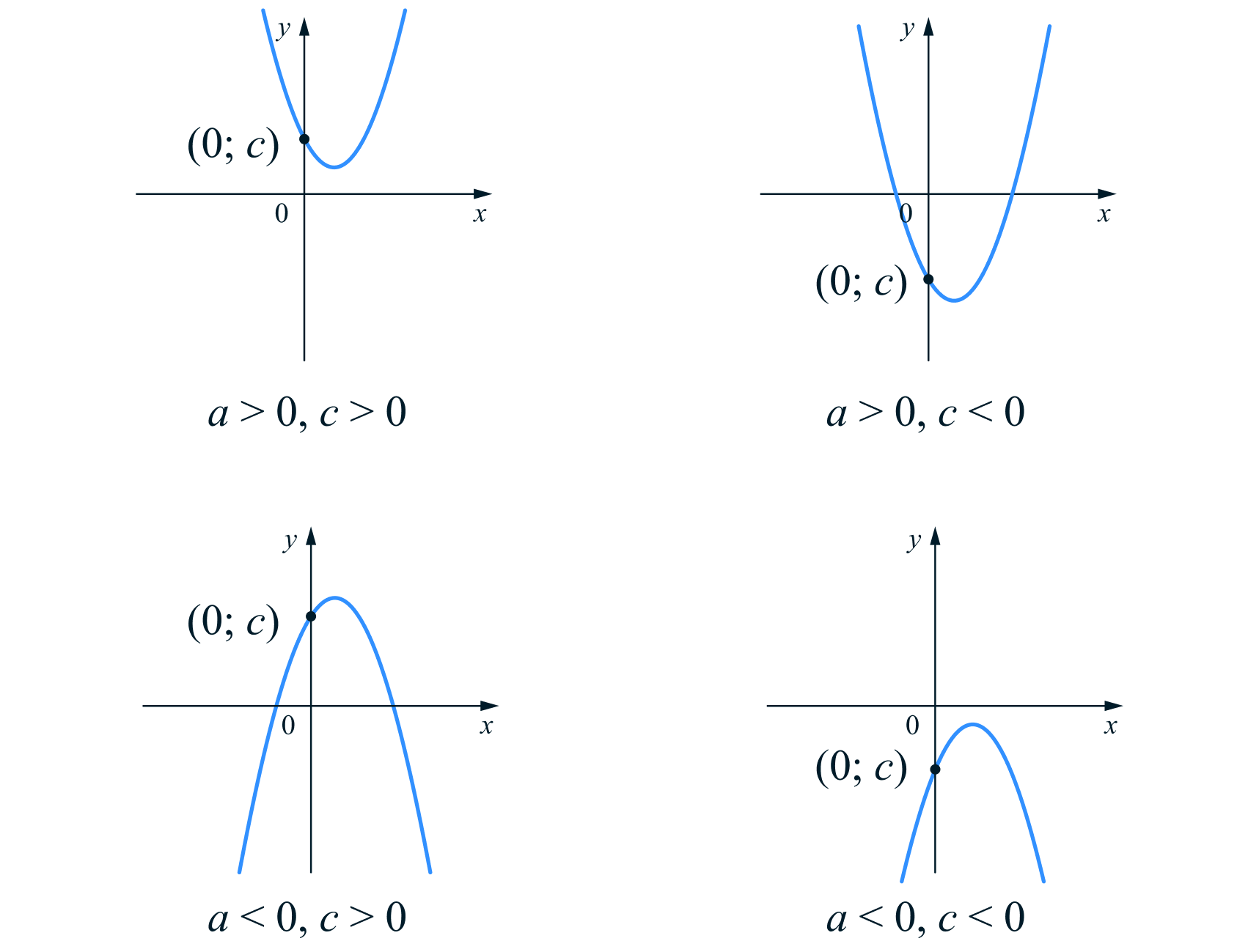
Чтобы найти точки пересечения графика с осью $Ox,$ нужно найти значения аргумента, при которых $y(x)= 0,$ то есть решить квадратное уравнение $ax2+ bx +c = 0.$

Таким образом,

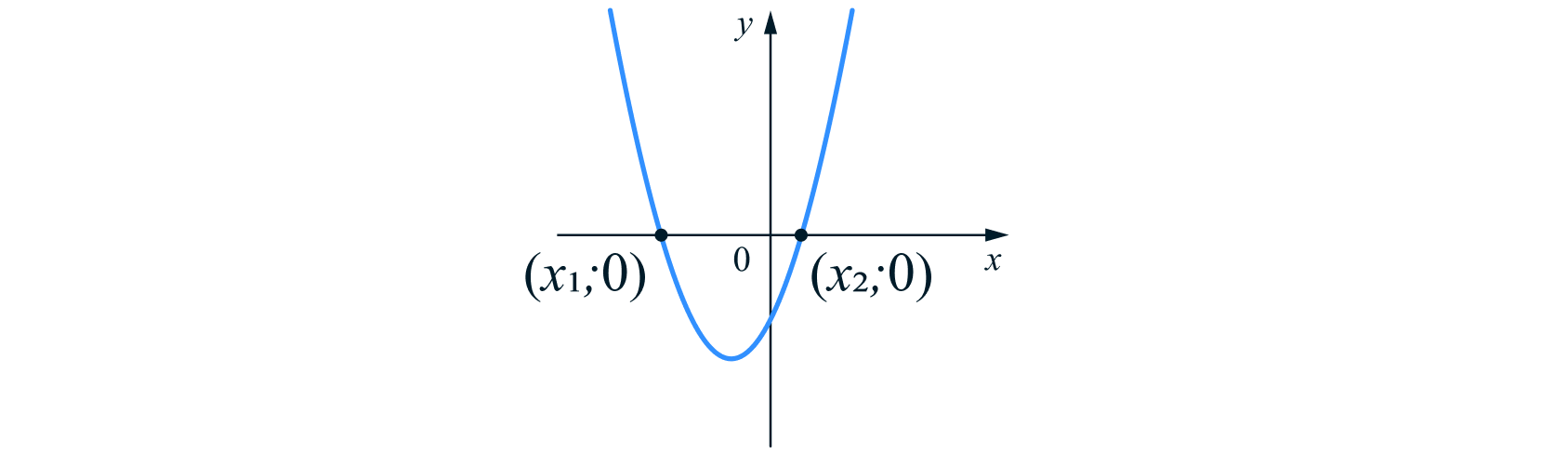
Если квадратное уравнение $2 ax + bx+ c= 0$ имеет два корня $(D > 0),$ то парабола пересекает ось $Ox$ в двух точках $(x1;0)$ и $(x2;0),$ где $x1$ и $x2$ — корни уравнения.

$PIC$
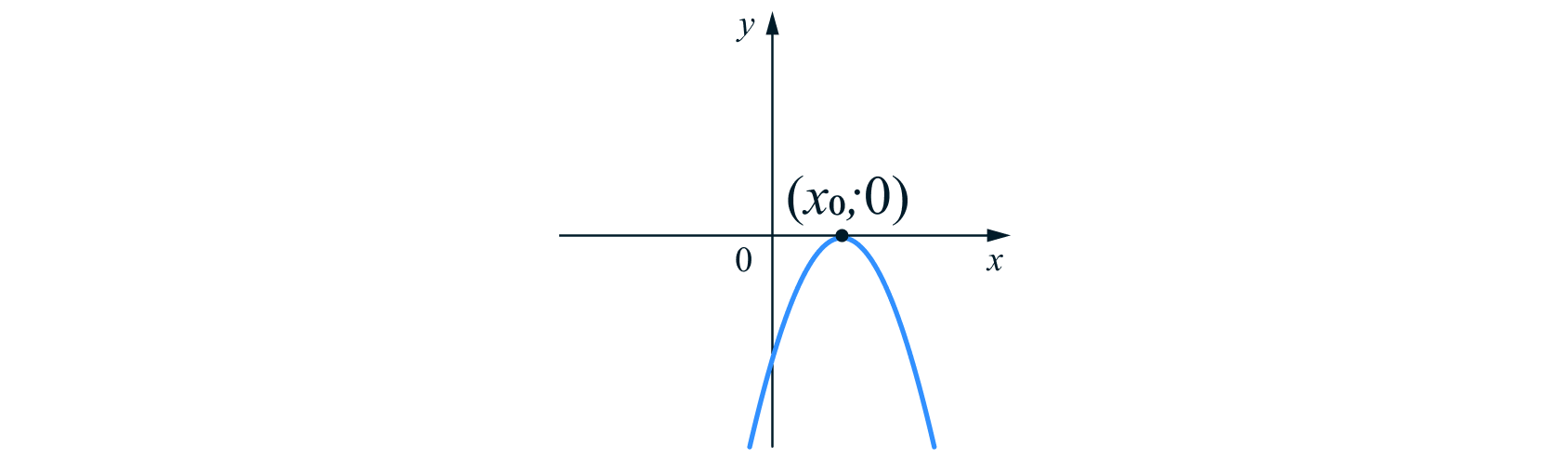
Если квадратное уравнение $2 ax +bx +c =0$ имеет один корень $(D = 0),$ то парабола касается оси $Ox$ в точке $(x0;0),$ где $x0$ — корень квадратного уравнения, он же будет вершиной параболы.

$PIC$
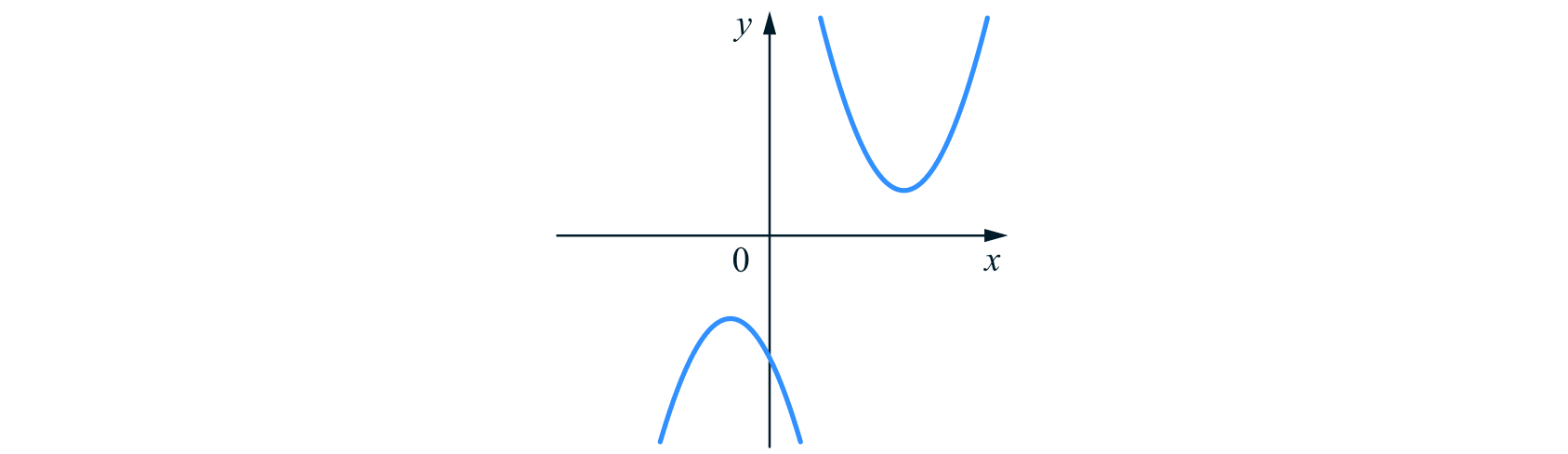
Если квадратное уравнение не имеет корней $(D < 0),$ то парабола не имеет общих точек с осью $Ox,$ то есть находится целиком выше оси $Ox$ при $a> 0$ и ниже оси $Ox$ при $a< 0.$

$PIC$

Перечислим еще раз все сведения о квадратичной функции:

$y = ax2+ bx+ c,$ где $a⁄= 0$ — квадратичная функция, её графиком является парабола.
Вершина параболы находится в точке $b −b2+ 4ac (− 2a-;--4a---).$
При $a> 0$ ветви параболы направлены вверх, при $a< 0$ ветви параболы направлены вниз.
Прямая $b x= − 2a-$ является осью симметрии параболы.
Парабола пересекает ось $Oy$ в точке $(0;c).$
Чтобы найти точки пересечения параболы с осью $Ox,$ нужно решить квадратное уравнение $ax2+ bx+ c= 0.$
При $D >0$ парабола пересекает ось абсцисс в двух точках.
При $D =0$ парабола касается оси абсцисс.
При $D <0$ парабола не имеет общих точек с осью абсцисс.

Предыдущая справка

Следующая справка