Математика в физике

Гипербола

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Математика в физике

Теоретическая справка

#888

Гипербола

Функцию вида $y = k , x$ где $k ∈ R,$ $k ⁄= 0,$ называют обратной пропорциональностью.

Графиком функции $k y = x$ является гипербола.

Свойства обратной пропорциональности

Исследуем свойства функции $f(x)= 1x ,$ а затем построим график этой функции.

Так как делить на ноль нельзя, область определения функции— множество всех действительных чисел, исключая число ноль. $D(f)= (−∞; 0)∪ (0;+ ∞ ).$
Рассмотрим любое число $a⁄= 0,$ функция примет значение $a,$ если взять $x = 1. a$ Значение $0$ функция не принимает. Тогда множество значений функции— множество всех действительных чисел, исключая ноль. $E(f)= (− ∞;0)∪ (0;+ ∞).$
Функция не ограничена, она не имеет ни наибольшего значения, ни наименьшего значения.
Функция является нечетной, так как $1 1 f(−x) = −x-= −x = −f(x).$
Тогда её график симметричен относительно начала координат.
Функция непериодическая.
Точки пересечения графика функции с осями координат:
Для того, чтобы найти точку пересечения графика функции с осью $Oy,$ нужно найти значение функции в точке $x= 0.$ Функция $y =-1 x$ не определена в точке $x= 0,$ тогда график функции не пересекает ось $Oy.$
Для того, чтобы найти точки пересечения графика функции с осью $Ox,$ нужно найти при каких значениях аргумента значение функции равно нулю, то есть решить уравнение $f(x)= 0.$ Так как уравнение $1 x = 0$ не имеет решений, то график функции не пересекает ось $Ox.$
Таким образом, график функции $y = 1 x$ не пересекает координатные оси.
У функции нет нулей.
Функция принимает положительные значения на промежутке $(0;+ ∞),$ и отрицательные значения на промежутке $(− ∞;0).$
Тогда функция $1 f(x)= x$ будет расположена в первой и третьей координатных четвертях.
Рассмотрим функцию $f(x)= 1 x$ на промежутке $(0;+ ∞).$
Если $0 < x1 < x2,$ то $1-> -1, x1 x2$ так как из двух положительных дробей с одинаковыми числителями больше та, знаменатель которой меньше.
Таким образом функция обратной пропорциональности $1 f(x)= x$ убывает на промежутке $(0;+∞ ).$
Теперь рассмотрим функцию $1 f(x)= x$ на промежутке $(−∞; 0).$
Аналогично, если $x1 < x2 < 0,$ то $1 1 x1 > x2.$
Таким образом функция обратной пропорциональности $1 f(x)= x$ убывает на промежутке $(− ∞;0).$
Функция $f(x) = 1 x$ имеет вертикальную ассимтоту $x = 0$ и горизонтальную ассимптоту $x= 0.$ Это свойство мы объясним, когда будем строить график.

Построим таблицу значений для нескольких точек:


$x$	$− 2$	$− 1$	$− 1 2$	$1 2$	1	2

$y$	$1 − 2$	$− 1$	$− 2$	2	1	$1 2$

Теперь, учитывая перечисленные свойства, можем построить график функции, через шесть найденных точек. Получаем следующий график:

$PIC$

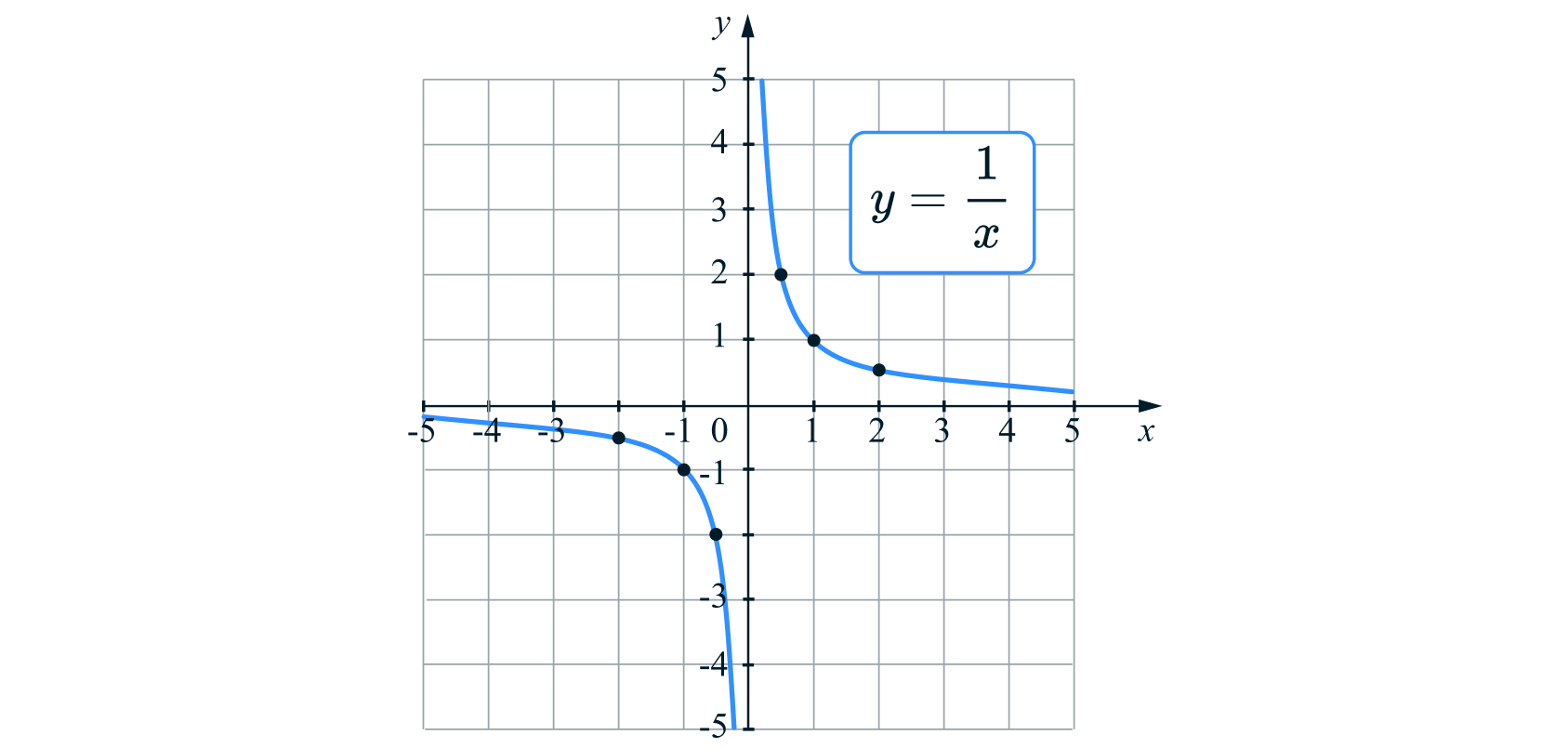
Эта кривая линия на плоскости, состоящая из двух ветвей, называется гиперболой.

Заметим, что

Если $x$ положителен и стремится к 0, то значение $1x$ стремится к $+∞.$ Так, например, при $x = 12,$ $y =2;$ при $x= -1, 10$ $y = 10;$ при $x = -1-, 100$ $y = 100$ и так далее. Тогда график прижимается к оси $Oy$ справа, то есть ось $Oy$ является вертикальной ассимтотой.
Аналогично, если $x$ отрицателен и стремится к 0, то значение $1 x$ стремится к $− ∞$ , а график прижимается к оси $Oy$ слева.
Если $x$ положителен и стремится к $+ ∞$ , то значение $1 x$ стремится к 0. Так, например, при $x= 10,$ $1 y = 10;$ при $x= 100,$ $y =-1-, 100$ при $x= 1000,$ $y = -1-- 1000$ и так далее. Тогда график прижимается к оси $Ox$ сверху, то есть ось $Ox$ является горизонтальной ассимтотой.
Аналогично, если $x$ отрицателен и стремится к $− ∞$ , то значение $1 x$ стремится к 0, а график прижимается к оси $Ox$ снизу.

Значит, прямые $x = 0$ и $y = 0$ являются асимптотами.

Предыдущая справка

Следующая справка