Механика

Работа. Энергия. Закон сохранения энергии

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Механика

Теоретическая справка

#960

Работа силы

Работа силы — скалярное произведение вектора силы на вектор перемещения. По определению скалярного произведения работа силы — произведение модуля вектора силы на модуль вектора перемещения и на косинус угла между ними.

|--------------------| A-=-F⃗⋅ ⃗S-=-F-⋅S-⋅cosα-

Единицы измерения:

$[A] = Н ⋅м = Дж$ — джоуль.

Зависимость работы от направления силы:

Мощность

Мощность — скалярная величина, характеризующая скорость совершения работы, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

|------| | A | N = t-| --------

Единицы измерения:

$[N] =$ Вт — ватт.

При неизменной силе $F⃗− const$ справедливы следующие рассуждения.

ΔA N = -Δt-

A = FS cosα

Подставляя выражение работы в выражение мощности, имеем:

Δ(F-Scosα)- ΔS- N = Δt = F cosα Δt

По определению $ΔS --- = v Δt$ , следовательно, мгновенная мощность:

|------------| -N-=-F-vcosα-|

Коэффициент полезного действия

Коэффициент полезного действия (КПД) — физическая величина, равная отношению полезной работы (мощности) к затраченной.

|--------------------------| | A-пол Pпол | η = A зат ⋅100% = Pзат ⋅100%| ----------------------------

Единицы измерения:

$[η] = %$ — проценты.

$[η] =$ доли единицы (для перевода в доли единицы необходимо проценты поделить на 100 $%$ ).

КПД показывает, какая часть энергии переводится в пользу. КПД не может быть больше 100 $%$ или 1.

Силы в природе

Силы в природе можно классифицировать на два вида:

Консервативные (потенциальные) силы — силы, сохраняющие механическую энергию замкнутой системы тел. Работа консервативных сил не зависит от формы пути между двумя точками (при перемещении тела между ними), а зависит лишь от начального и конечного положения тела. Работа потенциальной силы по замкнутой траектории равна нулю.
Примеры: сила тяжести, сила упругости, сила гравитации, сила Кулона.
Диссипативные силы — силы, которые рассеивают механическую энергию. Работа диссипативной силы зависит от траектории движения тела и по замкнутой траектории не равна нулю.
Примеры: сила трения, сила сопротивления, сила натяжения.

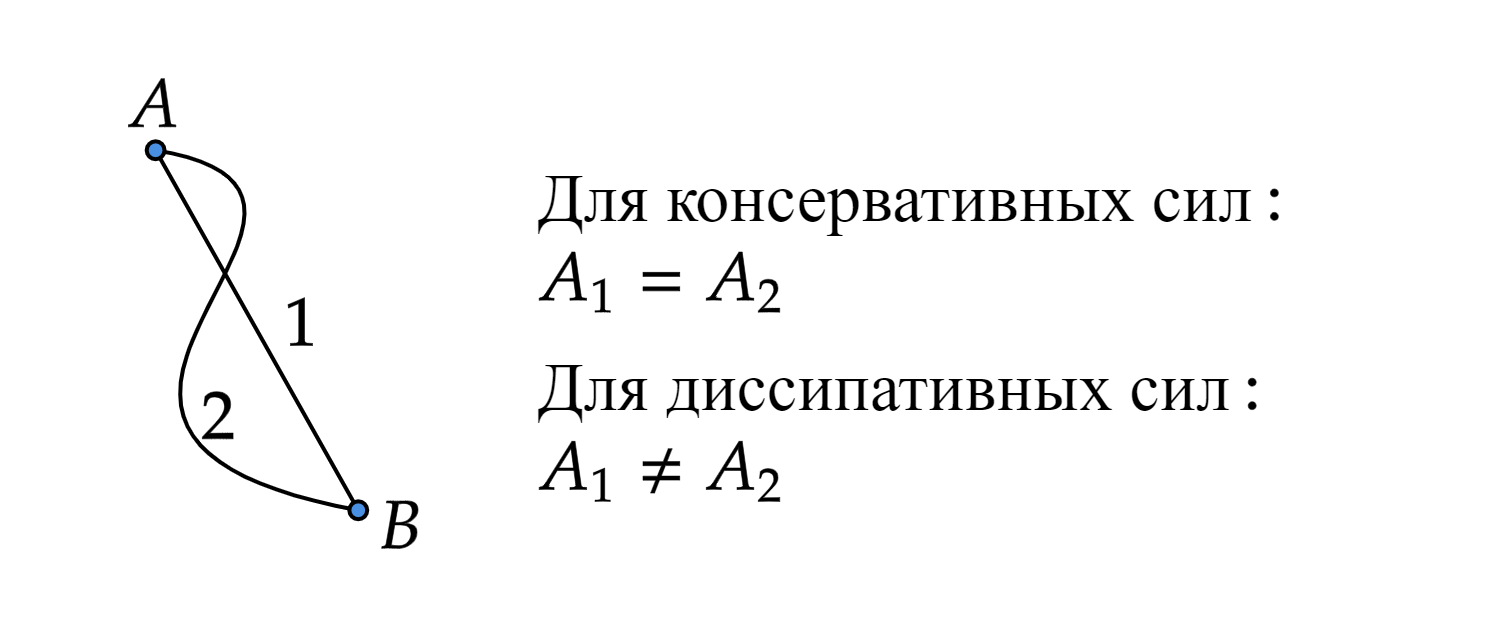
Энергия

1. Кинетическая энергия

Кинетическая энергия обусловлена движением тела.

|----------| | mv2-| E-кин-=--2---

Единицы измерения:

$[Eк] =$ Дж — джоуль.

Зная, что импульс $p = mv$ , а также домножив и поделив на $m$ , имеем:

|----------| m2v2 | p2 | Eкин = -2m--- ⇒ |Eкин = 2m-| -----------

Теорема о кинетической энергии

Формулировка: изменение кинетической энергии тела равно работе всех сил, действующих на тело.

∑n ΔE кин = AF1 + AF2 + ...+ AFi = AFi i=1

2. Потенциальная энергия

Потенциальная энергия зависит от взаимного положения тел в системе, которое изменяют консервативные силы.

|--------------------|--------------|----------------------| |Консервативная-сила-|---Форм-ула----|П-отенциальная энергия| | С ила тяж ести | Fтяж = mg | Eпот = mgh | |--------------------|--------------|-------------kx2------| |--С-ила уп-ругости---|--Fупр-=-− kx--|------Eпот =--2-------| | | M-m- | M-m- | |Гравитационная-сила-|Fграв =-G-R2--|----Eпот =-−-G-R------| | Сила Кулона |FКул =--1- Qq-| Eпот = -1--Qq- | ----------------------------4π-𝜀0-r2-------------4π𝜀0-r------

Единицы измерения:

$[Eпот] =$ Дж — джоуль.

Величина потенциальной энергии может быть определена с точностью до произвольной постоянной, значение которой зависит от выбора нулевого уровня. Нулевой уровень — положение тела, в котором потенциальную энергию, которой оно обладает, условно принимают за ноль.

В отличие от кинетической энергии, потенциальная энергия может принимать отрицательные значения, если тело находится ниже нулевого уровня.

Теорема о потенциальной энергии

Формулировка: работа потенциальной силы определяется как разность потенциальных энергий («было» минус «стало»).

|--------------------| -Aпот =-E-пот.н. −-Eпот.к.

Рассмотрим, как работает данная теорема на примере силы тяжести.

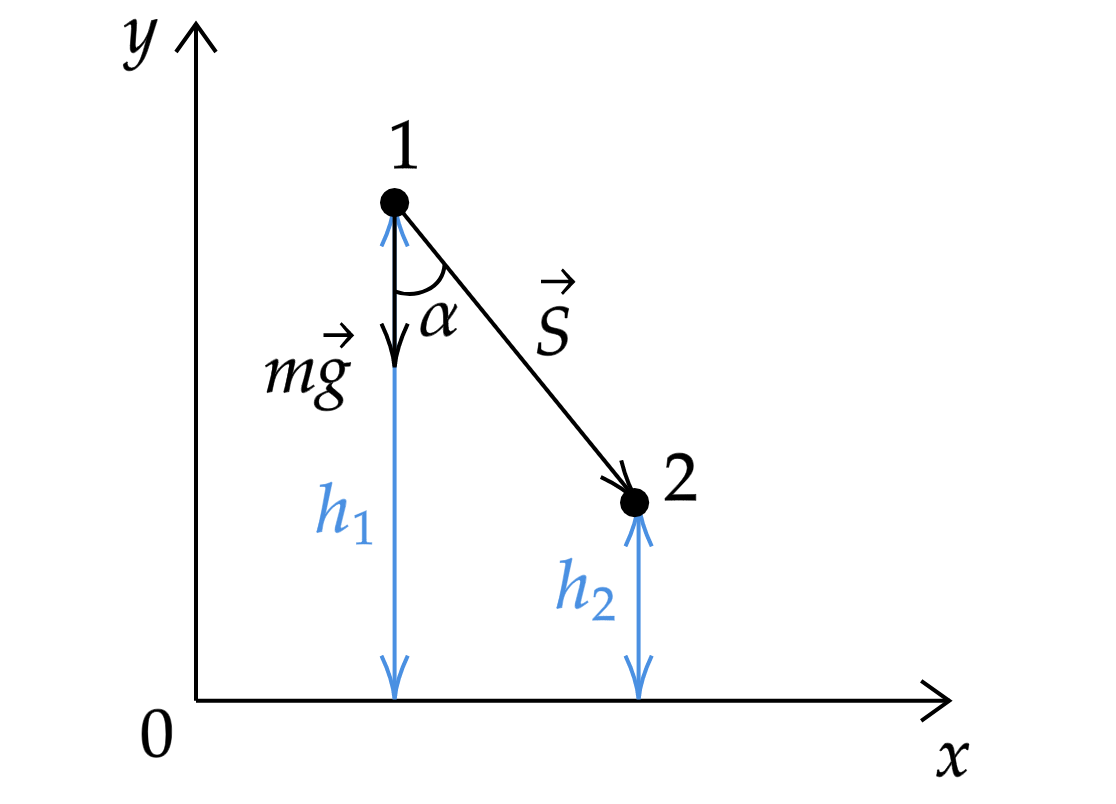
Пусть тело массой $m$ переместилось из положения 1 в положение 2. Работу силы тяжести в положении 1 можно найти по уже известной нам формуле:

Amg = mgS cosα

Теперь воспользуемся теоремой о потенциальной энергии и найдем работу той же силы тяжести с учетом того, что $E пот = mgh$ :

A = mgh − mgh = mg(h − h ) mg 1 2 1 2

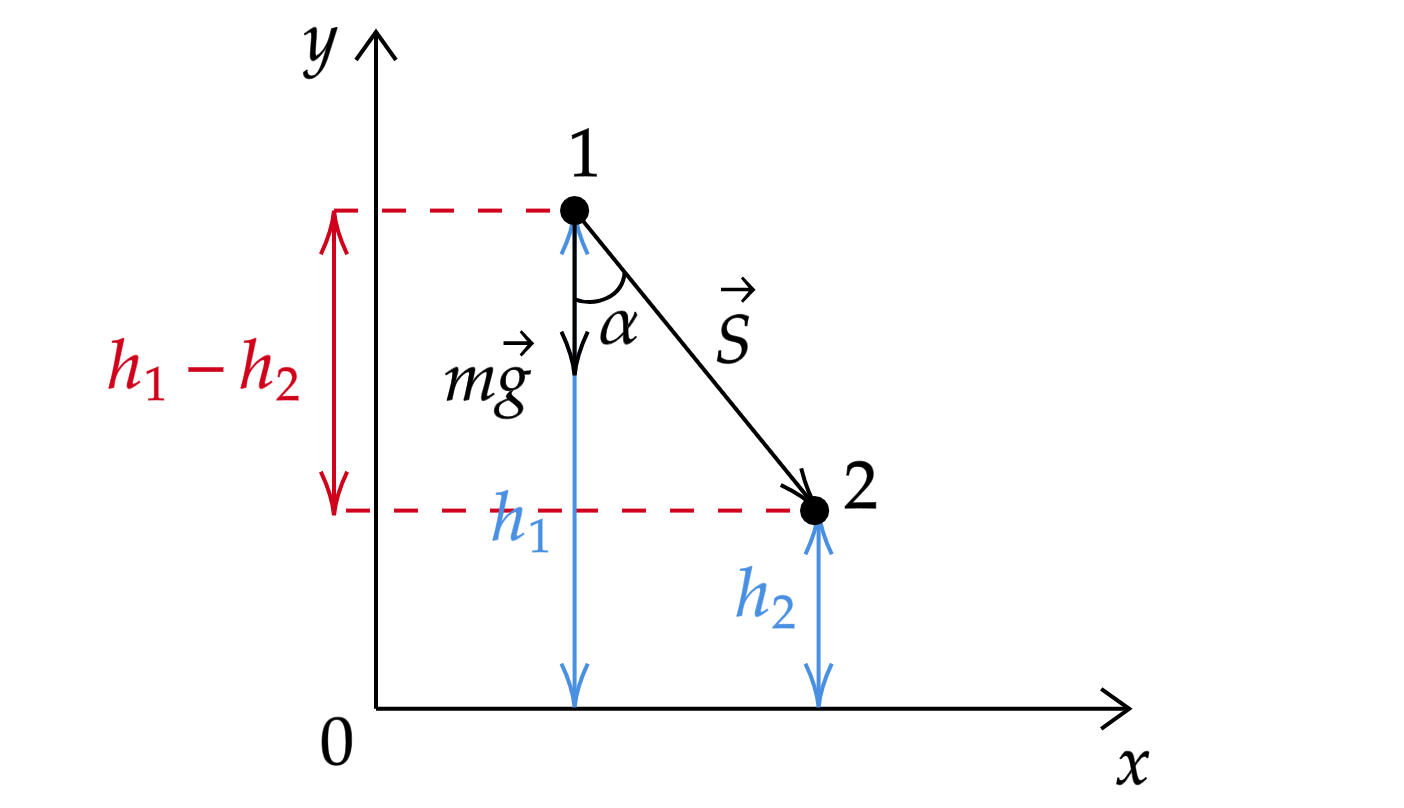
Также можно заметить, что $(h1 − h2) = Scosα$ , тогда:

Amg = mgS cosα

Таким образом, мы вывели связь между общей формулой для работы и формулой для работы потенциальных сил.

Закон сохранения механической энергии

Вспомним теорему о кинетической энергии:

n∑ ΔE кин = AFi i=1

Разобьем сумму всех сил на суммы потенциальных и непотенциальных сил:

∑n пот ∑n непот ΔE кин = A Fi + A Fi i=1 i=1

Если сумма работ всех непотенциальных сил равна нулю $n∑ непот A Fi = 0 i=1$ , то:

∑n пот ΔE кин = A Fi i=1

Вспомним теорему о потенциальной энергии и подставим ее в предыдущее выражение: $A пот = Eпот.н.− E пот.к.$ .

∑n ΔE кин = Eкин.к − E кин.н = (E пот.н.i − E пот.к.i) = 0 i=1

Таким образом, мы вывели закон сохранения механической энергии:

|------------------------------------------| | ∑n ∑n | E кин.к + i=1Eпот.к.i = E кин.н + i=1 Eпот.н.i = const --------------------------------------------

Формулировка: сумма кинетической и потенциальной энергии в конце равна сумме кинетической и потенциальной энергии в начале и есть величина неизменная в том случае, если работа всех непотенциальных сил равна нулю.

Предыдущая справка

Следующая справка