Механика

Импульс. Закон сохранения импульса

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Механика

Теоретическая справка

#962

Импульс — векторная физическая величина, численно равная произведению массы на скорость. Импульс есть количественная характеристика движения.

|------| ⃗p-=-m-⃗v-

Единицы измерения:

$[p] =$ кг $⋅$ м/с

Второй закон Ньютона в импульсной форме

Запишем второй закон Ньютона согласно основной его формулировке:

F⃗1 + ⃗F2 + ...+ F⃗n = m ⃗a

Распишем ускорение по определению:

Δ⃗v F⃗1 + ⃗F2 + ...+ F⃗n = m Δt

Рассмотрим отдельно правую часть. Распишем изменение скорости и раскроем скобки:

Δ⃗v- m-(⃗vк −-⃗v0) m⃗vк-− m-⃗v0 m Δt = Δt = Δt

Выражения $m ⃗vк$ и $m ⃗v0$ есть не что иное, как конечный и начальный импульс системы:

⃗pк − ⃗p0 ⃗F1 + ⃗F2 + ...+ F⃗n =-Δt---

Δ ⃗p F⃗1 + ⃗F2 + ...+ F⃗n =--- ⇒ Δ ⃗p = (⃗F1 + F⃗2 + ...+ ⃗Fn)Δt Δt

Таким образом, второй закон Ньютона в импульсной форме:

|----------| |Δ ⃗p = ⃗F Δt| -----------

Формулировка: изменение импульса тела равно векторной сумме импульсов сил.

Выражение $⃗FΔt$ называется импульсом силы.

Импульс системы тел

Рассмотрим систему из трех тел 1, 2, 3. Пусть все тела системы взаимодействуют друг с другом с некоторыми силами $⃗F12$ , $F⃗13$ , $⃗F21$ , $⃗F23$ и $F⃗31$ , $⃗F32$ .

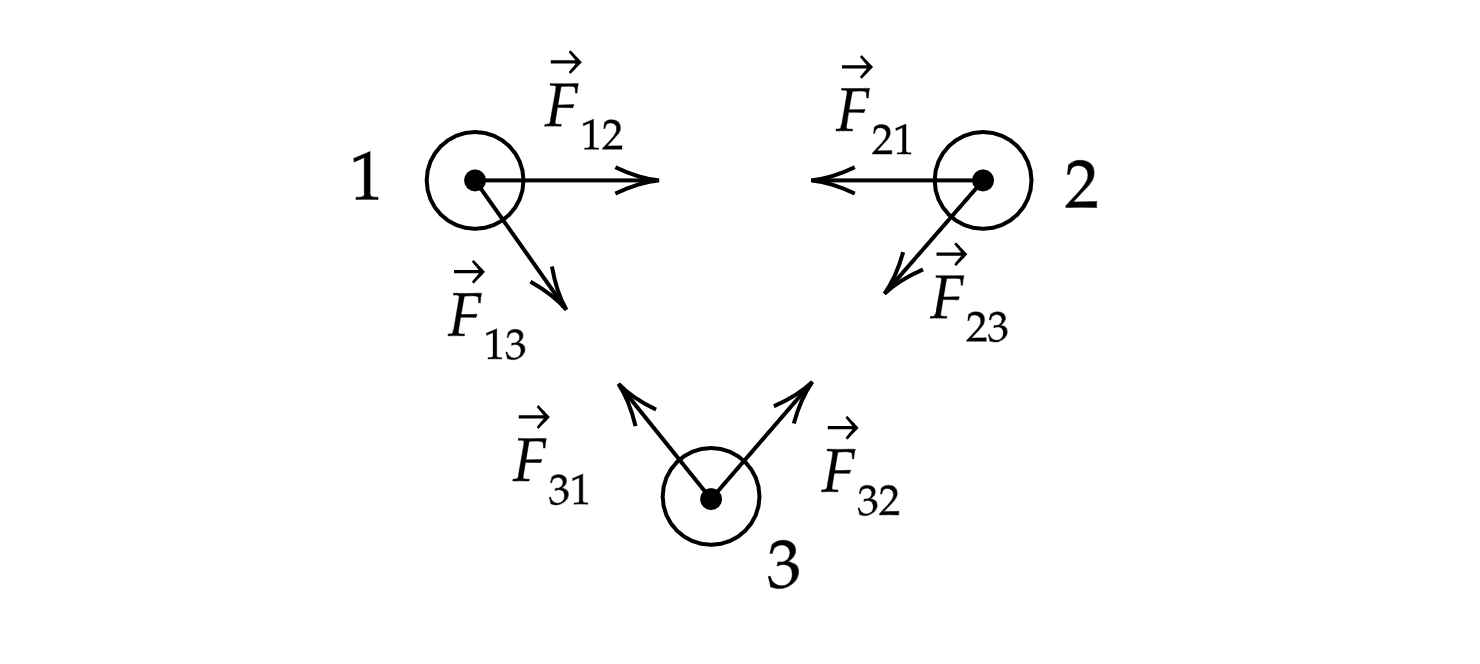
Выберем систему «поменьше», состоящую из тел 1 и 2. Внутренние силы — силы, которые появляются в результате взаимодействия тел внутри системы. Внешние силы действуют на тела системы со стороны внешних объектов. В данном случае $⃗F12$ и $⃗F21$ — внутренние силы, $⃗F13$ , $F⃗23$ — внешние силы.

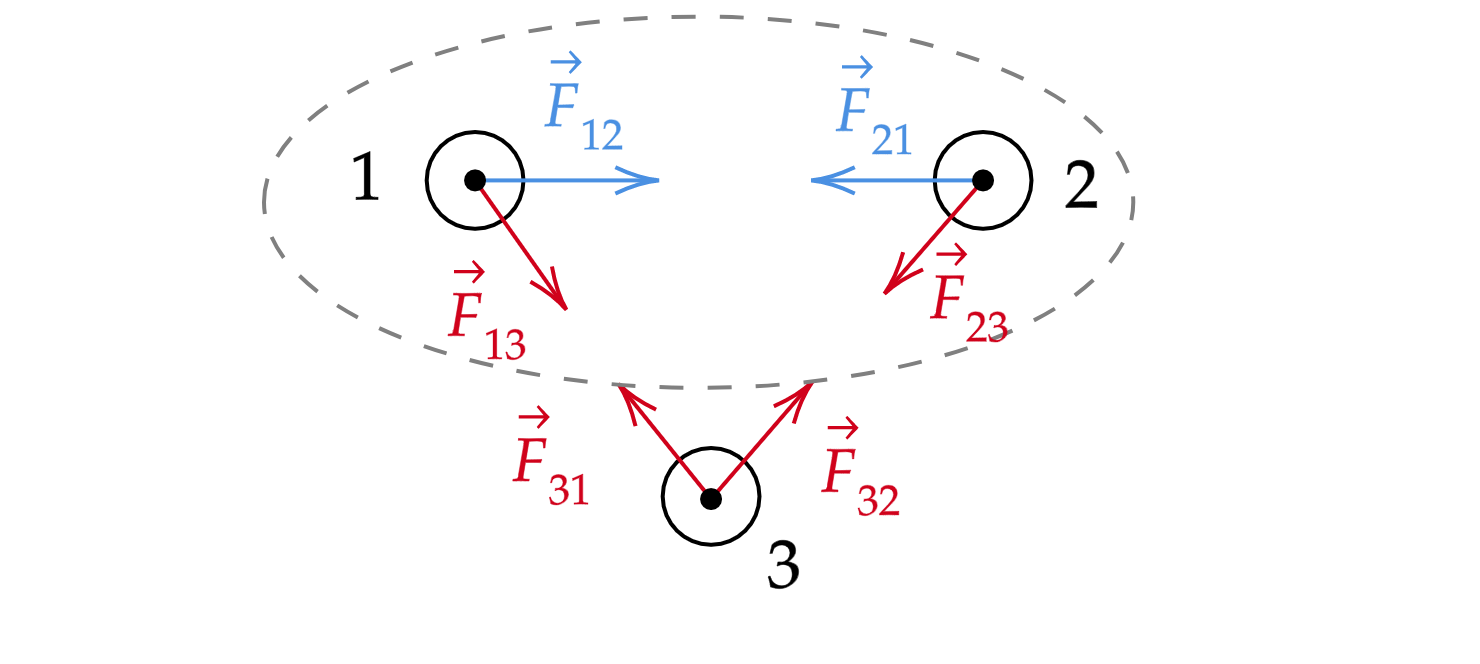
Запишем второй закон Ньютона в импульсной форме для тела 1 и 2 и просуммируем полученные уравнения.

Для первого тела: $Δ⃗p1 = (F⃗12 +F⃗13)Δt$ .

Для второго тела: $Δ⃗p2 = (F⃗21 +F⃗23)Δt$ .

Сумма: $Δ ⃗p1 + Δ⃗p2 = (⃗F12 + ⃗F13 + ⃗F21 + ⃗F23)Δt$ .

По третьему закону Ньютона векторная сумма внутренних сил $⃗ F12$ и $⃗ F21$ равна нулю. Величину $Δ⃗p1 + Δ⃗p2$ назовем изменением импульса системы $Δ ⃗pсист$ . С учетом этого: $Δ⃗pсист = (⃗F13 + ⃗F23)Δt$

В общем виде:

|--------∑-----------| |Δ ⃗pсист = ⃗Fвнеш ⋅Δt | ---------------------

Формулировка: изменение импульса системы равно векторной сумме импульсов внешних сил.

Закон сохранения импульса

Формулировка: импульс системы тел есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

|--------------------------| Δ ⃗pсист =⃗0 ⇒ ⃗pсист = co⃗nst ----------------------------

Закон сохранения импульса выполняется в следующих случаях:

1. Если векторная сумма внешних сил, действующих на систему, равна нулю:

F⃗ + ⃗F + ...+ ⃗F = ⃗0 внеш 1 внеш 2 внеш n

2. Если сумма проекций векторов внешних сил, действующих на систему тел, на некоторую ось равна нулю. Тогда импульс системы остается неизменным вдоль этой оси:

F1x + F2x + ...+Fnx = 0

3. Если на малом интервале времени внешние силы конечные и импульс этих сил за время действия во много раз меньше по величине импульса системы
$| | | | ||∑i ⃗Fi||Δt << ||⃗Pc(t)||$ , то следует, что приращение $ΔP⃗с$ импульса системы мало, т. е. на рассматриваемом интервале времени сохраняется импульс системы. Можно сказать и по-другому: если на малом интервале времени внешние силы во много раз меньше сил внутренних, то действием внешних сил можно пренебречь.

Предыдущая справка

Следующая справка