03 Динамика
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
На горизонтальной поверхности неподвижно закреплена абсолютно гладкая полусфера радиусом С её верхней точки из
состояния покоя соскальзывает маленькое тело. В некоторой точке тело отрывается от сферы и летит свободно.
Найдите время свободного падения тела от момента отрыва до падения на поверхность. Сопротивлением воздуха
пренебречь.
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень горизонтальной поверхности.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм ускорением, направленным к центру окружности вращения.
Решение
Во время скольжения тела по полусфере на него действуют сила тяжести и сила реакции
направленная вдоль
продолжения радиуса.Т.к. тело движется по окружности, то оно обладает центростремительным ускорением
направленное
к центру полусферы,
– скорость в какой-либо точке полусферы. Выберем удобные нам оси
и
Сделаем рисунок с указанием
сил, действующих на тело:
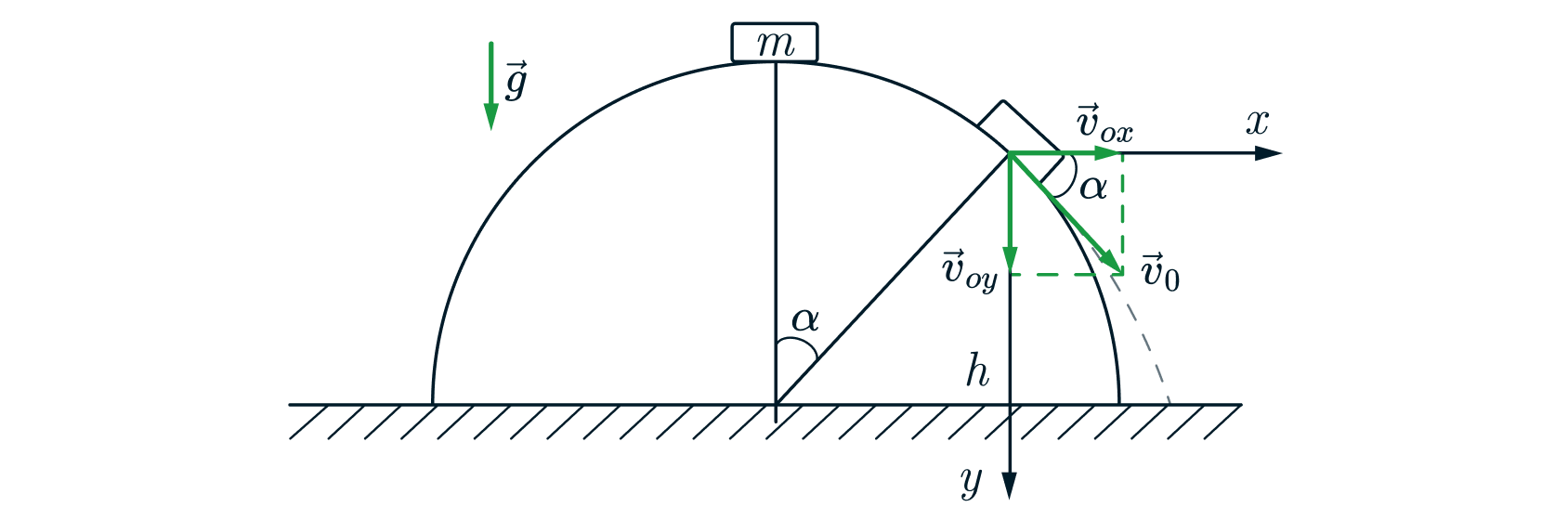
Спроектируем силы на ось по второму закону Ньютона получаем:
| (1) |
Так как скорость тела возрастает, то в некоторой точке обратится в ноль, т.е. тело оторвется от поверхности
полусферы.
Пусть высота, на которой происходит отрыв, равна Полная механическая энергия тела в верхней точке движения
. Полная механическая энергия в точке отрыва:
Так как трения нет, то полная механическая энергия
тела сохраняется:
| (2) |
Из рисунка найдём косинус угла :
| (3) |
Подставим значения и
из уравнений (2) и (3) в уравнение (1), получим:
В момент отрыва скорость тела:
C помощью тригонометрических формул найдём синус угла :
Теперь рассмотрим задачу с точки зрения кинематики. Сделаем рисунок с указанием начальных скоростей тела:
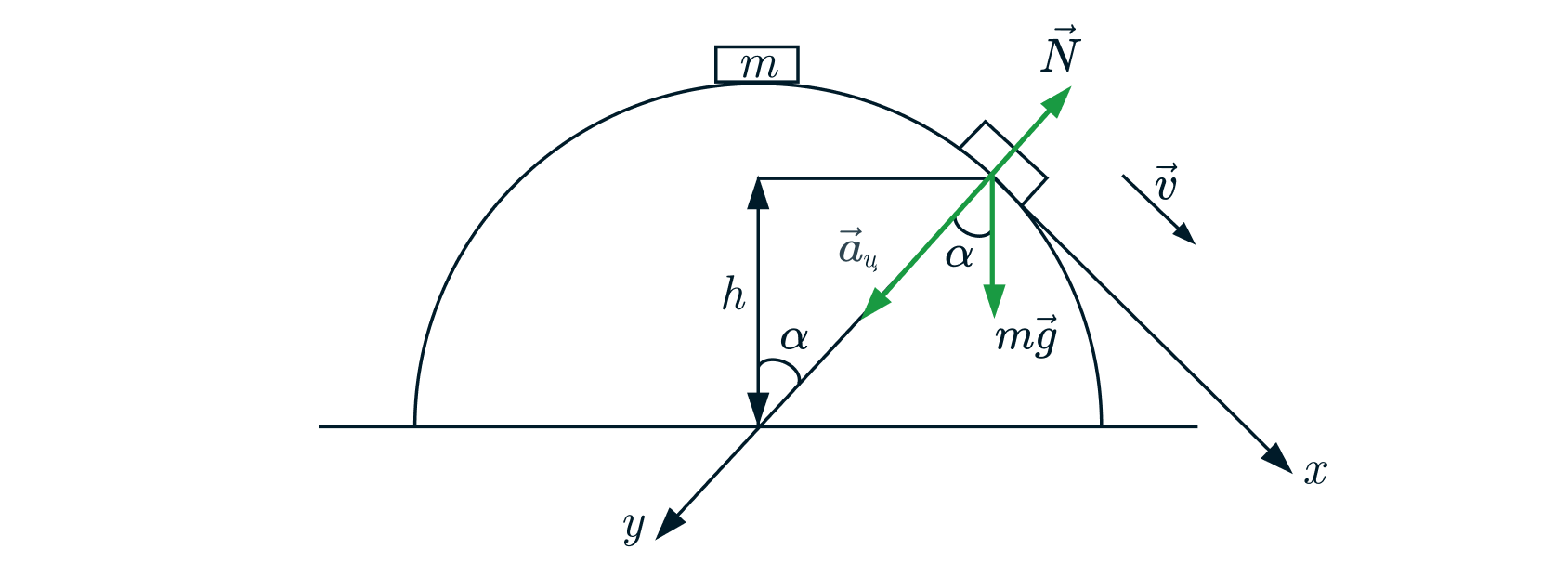
После отрыва от полусферы движение происходит только под действием силы тяжести, причем скорость тела сначала
направлена под углом
к горизонту. Значит, тело движется по параболе.
Начальные координаты тела:
Начальные скорости:
Закон движения по оси
:
В момент падения , где
- искомое время. Получаем квадратное уравнение:
корни которого:
Берем положительный корень:
Ошибка.
Попробуйте повторить позже
На горизонтальном столе доска массой на которую поместили брусок массой
Брусок и доска соединены
через идеальный блок (лёгкий, гладкий) лёгкой и нерастяжимой нитью. Брусок тянут с силой
Коэффициент трения
между доской и бруском равен
, а поверхность стола гладкая. Определите длину доски, если спустя время
брусок
соскальзывает с доски. Изначально брусок находился на краю доски. Обоснуйте применимость законов, используемых для решения
задачи.
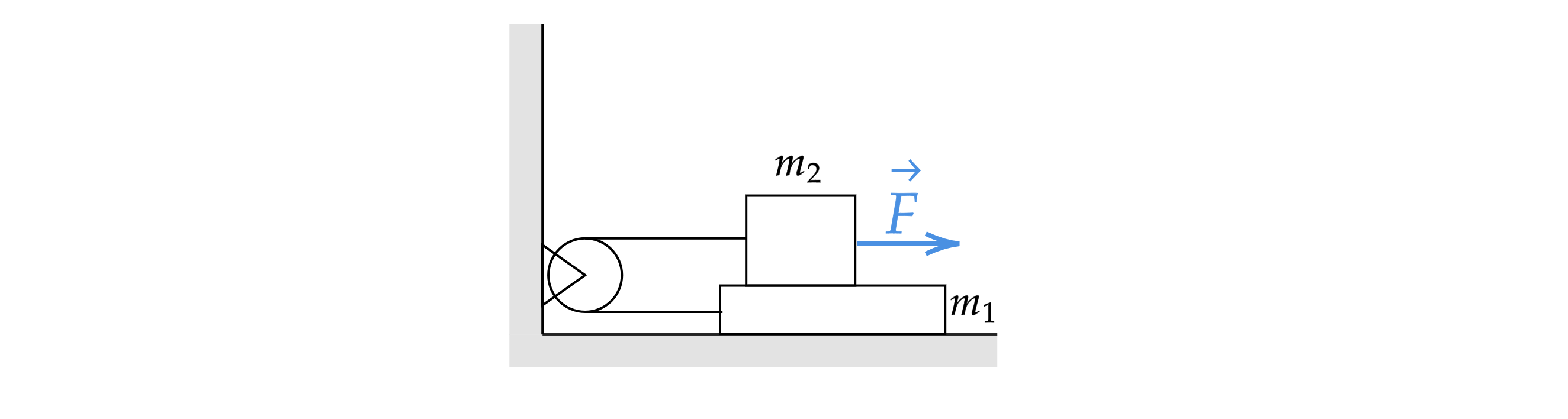
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Поскольку тела связаны нерастяжимой нитью их ускорения равны.
3. Поскольку тела связаны легкой нитью, блок идеальный и трение отсутствует, модули сил натяжения нитей, действующих на тела равны.
4. Поступательное движение тел в ИСО будем описывать при помощи законов Ньютона.
Рассмотрим задачу с точки зрения динамики:
Бруски движутся под действием сил, которые изображены на рисунке
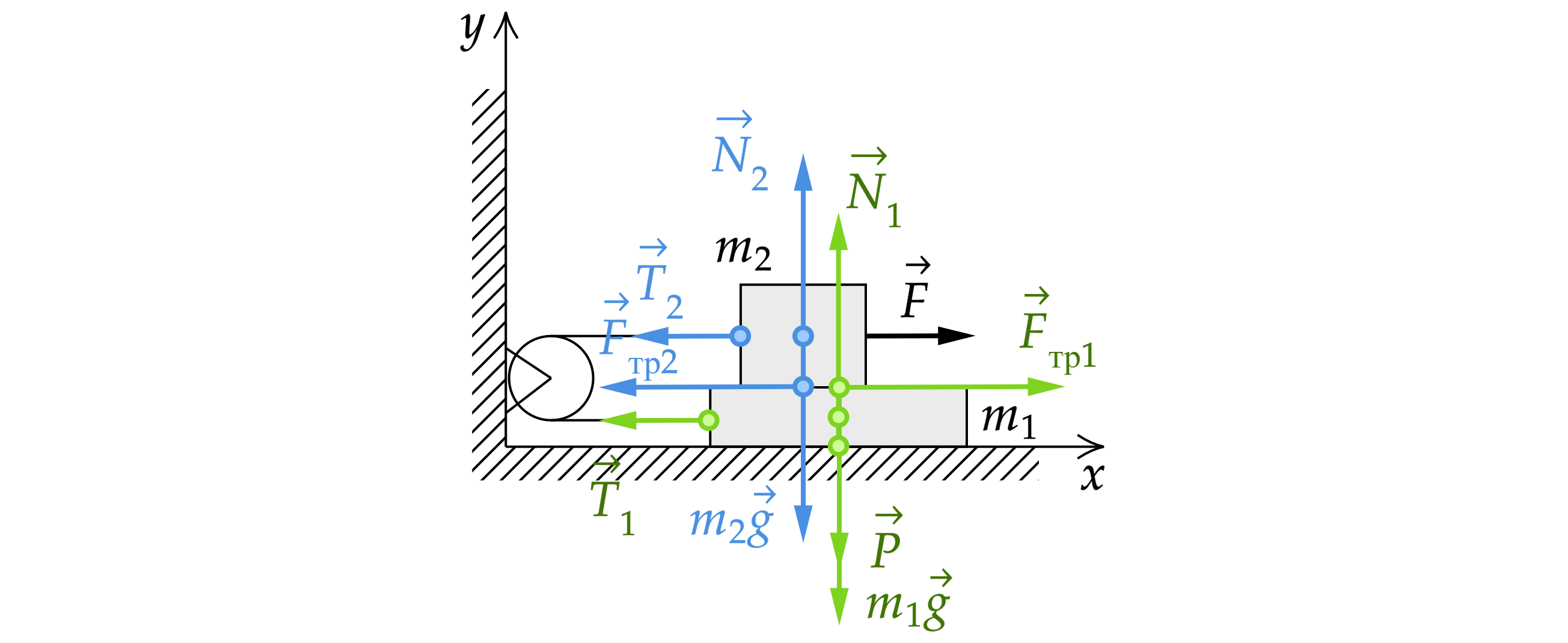
где и
– модули силы натяжения нити,
и
– модули силы трения,
и
– сила тяжести,
– сила
реакции опоры стола,
– сила реакции доски,
– вес бруска.
Запишем второй закон Ньютона для бруска и доски
Так как нить нерастяжимая, то . По третьему закону Ньютона
,
и
.
Спроецируем (1) на оси
и
|
|
Аналогично для (2)
|
|
Сила трения же равна
Тогда
|
|
Сложим два уравнения
Теперь применим кинематический подход:
Брусок двигается относительно доски равноускоренно и прямолинейно, тогда его движение описывается законом:
где – момент времени,
– координата бруска в момент времени
,
– скорость бруска в начальный момент времени,
–
ускорение бруска относительно доски (
).
В момент времени уравнение приобретёт вид:
Подставим формулу для ускорения в формулу для силы:
|
|
Ошибка.
Попробуйте повторить позже
Две гири массами 7 кг и 11 кг висят на концах нити, которая перекинута через блок. Через какое время после начала движения гирь каждая из них пройдет путь 10 см? Сделайте схематичный рисунок с указанием сил, действующих на брусок и груз. Обоснуйте применимость законов, используемых для решения задачи.
Источники:
Обоснование
1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.
2. Все тела движутся поступательно, поэтому их можно считать материальными точками.
3. Так как грузы являются материальными точками, то описывать их движение в ИСО будем, используя законы Ньютона.
4. Учитывая, что нить нерастяжима, блок идеальный, делаем вывод, что все тела движутся с одинаковым ускорением
5. Учитывая, что нить невесома, блок идеальный, делаем вывод, что силы натяжения, приложенные к телам, равны по модулю.
6. Так как тела движутся с ускорением, то описывать их движение будем с использованием формул кинематики равноускоренного движения.
Решение
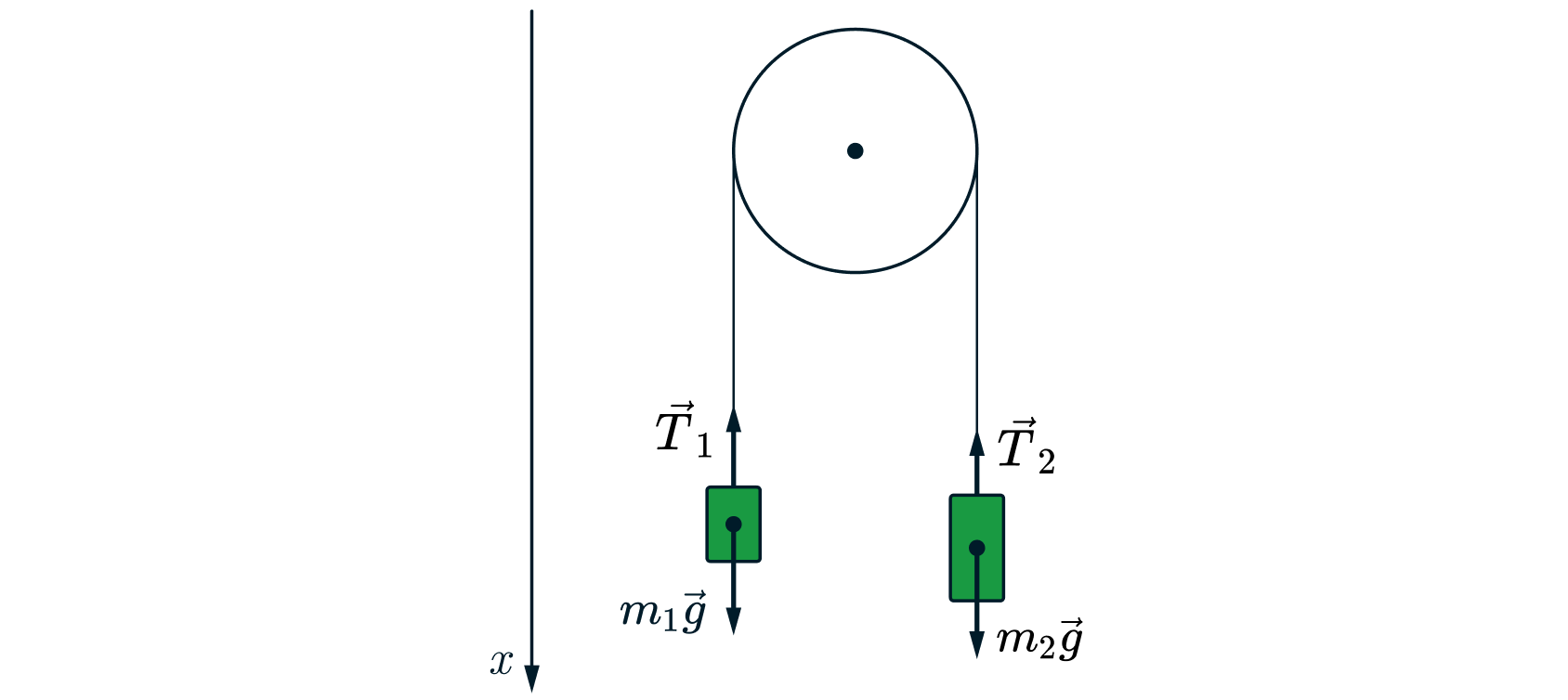
Запишем второй закон Ньютона для обоих тел в проекции на вертикальную ось:
Выразим в обоих случаях и приравняем:
Ускорение равно:
Пройденное расстояние равно:
Откуда выразим время:
Ошибка.
Попробуйте повторить позже
На горизонтальной гладкой поверхности стола покоится доска массой (см. рисунок). На доску со скоростью
въезжает шайба
массы
. Какой должна быть длина доски, чтобы шайба не соскользнула с неё? Коэффициент трения скольжения между шайбой и
доской равен
, размер шайбы мал по сравнению с длиной доски. Обоснуйте применимость законов, используемых для решения
задачи.

Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Шайба движется поступательно, поэтому её можно считать материальной точкой.
3. Так как шайба является материальной точкой, то описывать её движение в ИСО будем, используя второй закон
Ньютона.
4. Поскольку система является замкнутой и внешние силы на нее не действуют, применим закон сохранения импульса для описания
взаимодействия тел
5. На шайбу действуют потенциальная сила тяжести, сила реакции опоры и непотенциальная сила трения. Поскольку шайба
описывается моделью материальной точки, то работа силы трения равна изменению механической энергии
Решение
Когда шайба находится на доске на неё действует сила трения, направленная против скорости шайбы относительно доски.
Чтобы шайба не соскользнула с доски относительная скорость должна быть равна нулю, при этом длина доски
минимальна, если относительная скорость становится равной нулю в момент, когда шайба находится на краю доски.
Если относительная скорость равна нулю в конечный момент, значит скорости шайбы и доски равны в этот момент.
Пусть конечная скорость шайбы и доски – . По второму закону Ньютона для шайбы в проекции на вертикальную
ось:
Тогда сила трения, действующая на шайбу:
Путь, пройденный шайбой до остановки относительно доски, равен длине доски , поскольку останавливается она на краю
доски. Тогда работа силы трения:
Запишем закон сохранения проекции импульса на горизонтальную ось для системы тел "шайба+доска проекция импульса на эту ось сохраняется поскольку сила трения внутренняя сила для этой системы, внешние силы вдоль этой оси на систему не действуют:
Отсюда конечная скорость:
Запишем теорему об изменении кинетической энергии для той же системы тел:
Подставляя конечную скорость и выражая длину доски, получим:
Ошибка.
Попробуйте повторить позже
Призма находится на горизонтальной поверхности шероховатого стола (см. рисунок). На поверхность призмы, наклонённую под
углом к горизонту, положили брусок массой
и отпустили. Он стал соскальзывать, а призма осталась в покое. Коэффициент
трения скольжения между бруском и призмой равен
. Найти силу трения между призмой и столом. Обоснуйте применимость
законов, используемых для решения задачи.

Обоснование
1) Систему отсчета, связанную с Землей, будем считать инерциальной.
2) Движение бруска поступательное. Следовательно, его можно считать материальной точкой.
3) Движение призмы по горизонтальной поверхности поступательное. Следовательно, его можно описать моделью материальной
точки.
4) В ИСО для обоих тел (мат. точек) выполняется второй закон Ньютона.
5) Силы трения между бруском и призмой — парные, по третьему закону Ньютона эти силы равны по модулю в
ИСО. Вес бруска по третьему закону Ньютона равен силе реакции опоры, действующей на него со стороны призмы.
Решение
На брусок действуют: сила тяжести на брусок, сила трения со стороны призмы и сила нормальной реакции опопры призмы. На
призму действуют: сила тяжести на призму, сила давления со стороны бруска, сила трения со стороны бруска, сила нормальной
реакции опоры стола и сила трения со стороны стола. Запишем второй закон Ньютона для бруска в проекции на ось
перпендикулярно призме:
Сила трения между призмой и бруском:
По третьему закону Ньютона сила давления на призму со стороны бруска равна по модулю силе нормальной реакции опоры на брусок со стороны призмы. Запишем второй закон Ньютона для призмы в проекции на горизонтальную ось:
где – сила трения на призму со стороны стола.
Отсюда:
Ошибка.
Попробуйте повторить позже
Некоторое тело массой перемещают вверх по наклонной шероховатой плоскости с силой
. Какое ускорение будет у тела, если
сила направлена горизонтально (см.рисунок), угол наклона плоскости
, а коэффициент трения между плоскостью и телом
составляет
? Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.
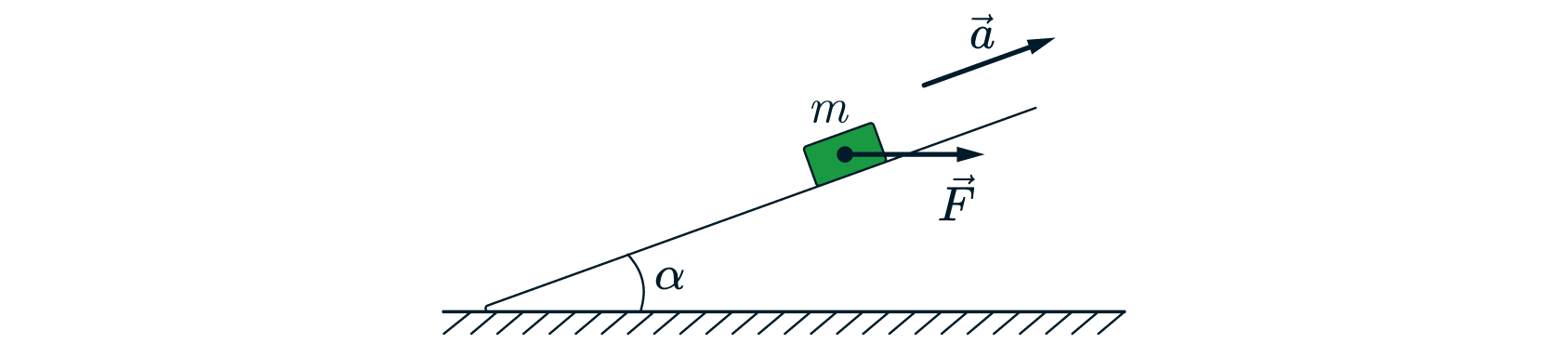
Источники:
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, можно считаеть его материальной точкой.
3. Так как тело является материальной точкой, то описывать нго движение в ИСО будем, используя законы Ньютона.
Решение
Обозначим все силы и оси на рисунке:
.png)
Запишем второй закон ньютона:
Спроецируем на оси:
Добавив формулу для силы трения скольжения, получим следующую систему:
Выразим из второго уравнения силу реакции опоры и подтавим в уравнение силы трения, получим:
Откуда выразим ускорение:
Ошибка.
Попробуйте повторить позже
На горизонтальном неподвижном столе лежит доска массой . На доске находится маленький брусок массой
.Брусок и доска связаны невесомой нерастяжимой нитью, перекинутой через невесомый блок, который закреплён на стене
(отрезки нити, не лежащие на блоке, горизонтальны). Коэффициент трения между бруском и доской
, между столом и
доской
. Доску тянут вправо горизонтальной силой
. Чему равен модуль силы
, если модуль ускорения бруска
относительно стола
? Трением в оси блока пренебречь. Сделайте рисунок с указанием сил, действующих на тела

Обоснуйте применимость законов, используемых для решения задачи.
Источники:
Обоснование 1. Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью стола.
2. Тела движутся поступательно, поэтому будем их описывать моделью материальной точки. Следовательно, можно использовать
второй закон Ньютона, сформулированный для материальных точек. Силы, действующие на тела, постоянны, поэтому движение
бруска и доски равноускоренно.
3. Так как нить нерастяжима, ускорения бруска и доски относительно стола равны по модулю и противоположны по
направлению:
4. Так как блок и нити невесомы и трением в оси блока можно пренебречь, то силы натяжения нити, действующие на доску и брусок, одинаковы:
5. Силы трения, действующие на брусок и доску, равны друг другу и противоположны по направлению по третьему закону Ньютона:
6. Модули сил нормальной реакции доски и давления бруска на доску
также равны друг другу по третьему закону
Ньютона:
Решение
1) Укажем силы, действующие на брусок (красным) и на доску (синим).
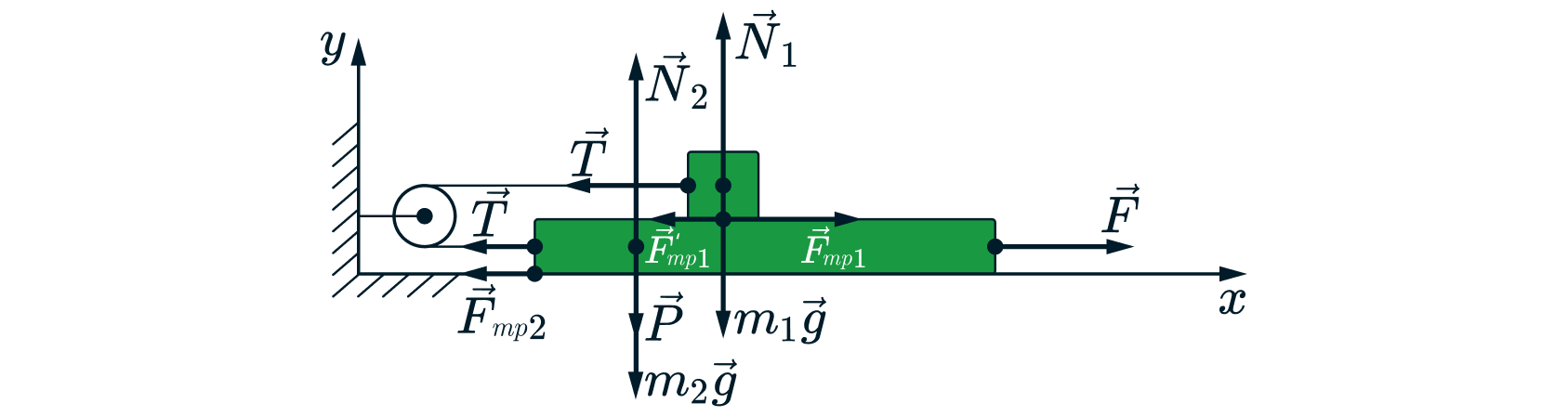
Здесь – сила натяжения нити,
– сила реакции опоры доски,
– сила реакции опоры стола,
– сила трения между
доской и бруском,
– сила трения между столом и доской.
Ускорения доски и бруска равны, так как они связаны нерастяжимой нитью.
Запишем второй закон Ньютона для доски и бруска
Здесь – ускорение,
по 3 закону Ньютона.
Сила трения равна:
Спроецируем второй закон Ньютона на вертикальную ось:
Спроецируем второй закон Ньютона на горизонтальную ось, с учётом (1):
|
|
Сложим два уравнения:
Отсюда выразим :



