Тема 11. Задачи на свойства графиков функций

11.11 Сложные комбинации нескольких графиков

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи на свойства графиков функций

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#87308

На рисунке изображены графики функций $f(x)= a|x− b|+ c$ и $g(x)= kx +d.$ Найдите абсциссу точки пересечения графиков функций $f(x)$ и $g(x).$

$xy110$

Показать ответ и решение

На рисунке видно, что вершина «уголка» модуля имеет координаты $(3;2).$ Также по картинке видно, что ветви уголка направлены вниз, значит, функция имеет вид

f(x)= a|x− 3|+ 2

При этом $a <0.$ По картинке видно, что в точке $x= − 2$ значение функции равно 0. Для того, чтобы попасть в точку $(− 2;0)$ из вершины с координатами $(3;2),$ нужно сместиться на 5 влево и на 2 вниз. Тогда понятно, что перед нами график функции $2 y = −5|x|,$ вершину которого сместили из точки $(0;0)$ в точку $(3;2).$ Значит, теперь мы полностью восстановили нашу функцию, она имеет вид

f(x)= − 2⋅|x− 3|+ 2 5

На рисунке видно, что график прямой $g(x)$ проходит через точки $(5;0)$ и $(2;−2).$ Тогда имеем систему:

$pict$

Значит, функция имеет вид

2 10 g(x)= 3x− 3

На рисунке видно, что график $g(x)$ пересекает график $f(x)$ при $x> 3.$ Значит, нужно искать корень уравнения

− 2(x − 3) +2 = 2x− 10 5 3 3 − 2 x+ 6+ 10 = 2x − 10 5 5 5 3 3 16-+ 10= 2 x+ 2x 5 3 3 5 48+ 50= 10x+ 6x 98= 16x x = 6,125

Ответ: 6,125

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#39634

На рисунке изображены графики функций $f(x) =ax2 +bx+ c$ и $---- |g(x)|= k√x +r,$ которые пересекаются в точках $A(−1;0),$ $B (0;− 2),$ $C (3;−4)$ и $D (x0;y0).$ Найдите $y0.$

$xy110ABC$

Показать ответ и решение

Найдем уравнения каждой функции. Пусть $---- g1(x)= k√x+ r,$ $---- g2(x)= −k√x + r$ — функции, задающие второе уравнение условия. Тогда график $g2(x)$ проходит через точки $A$ и $B$ , следовательно,

{0 = −k√ −1+-r- {r = 1 −2 =− k√0+-r ⇔ k = 2

Следовательно,

√ ----- |g(x)|= 2 x+ 1

График $f(x)= ax2 +bx +c$ проходит через точки $A,B,C :$

( ( 1 |{ 0= a− b+ c |{ a= 35 |( −2= c ⇔ |( b= −3 −4= 9a+ 3b+ c c= −2

Следовательно,

f(x)= 1x2− 5x − 2 3 3

Найдем четвертую точку пересечения, то есть корень $x0 ⁄= −1; 0; 3$ уравнения $f(x)= |g(x)|.$ По картинке можно предположить, что точка $D$ — общая для графиков $f(x)$ и $g1(x).$ Тогда имеем:

x2 − 5x − 6 = 6√x-+-1 √----- √----- (x − 6)(x+ 1)= 6√x-+1-|: x +1 ⁄= 0 (x− 6) x+ 1= 6 (x− 6)2(x +1)= 36 3 2 x − 11x + 24x = 0 |:x ⁄=0 x2− 11x+ 24= 0

Корни последнего уравнения $x =3; 8.$ Мы ищем корень $x0 = 8.$ Тогда

√ ---- y0 = g1(8)= 2 8+ 1= 6

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 3#75429

Даны функции $f(x)= −2x3− x2+ x− 2$ и $g(x)= 0,5(x− 2)2+ b.$ Определите, при каком значении $b$ графики $f(x)$ и $g(x)$ касаются в точке с положительной абсциссой.

Показать ответ и решение

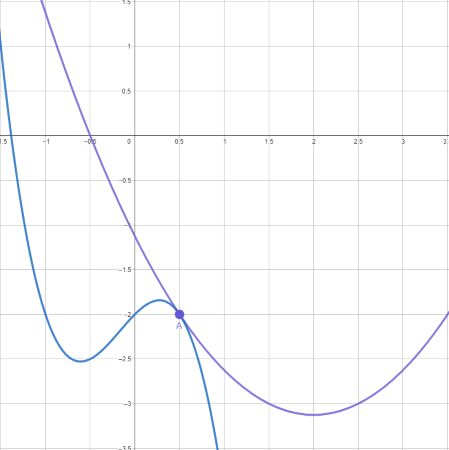
Пусть графики функций пересекаются в точке $A.$ Тогда для выполнения касания в ней нам требуется записать систему из трёх условий — о равенстве значений функций в точке $A$ и равенстве значений производной в этой же точке (ну и помним про положительность абсциссы):

$pict$

Рассмотрим последнее уравнение системы отдельно:

−2 ⋅3 ⋅x3−1 − 2 ⋅x2−1+ 1⋅x1−1− 0= 0,5⋅2⋅(x− 2)2−1, 2 − 2x − x + 1= 0, −(x− 0,5)(x + 1) =0.

Помня об условии $x >0,$ оставляем корень $x = 0,5.$ Подставим его во второе уравнение системы и получим ответ:

3 2 2 −2⋅(0,5) − (0,5) +0,5− 2= 0,5⋅(0,5− 2)+ b, b= −3,125.

$PIC$

Ответ: -3,125

Ошибка.
Попробуйте повторить позже

Задача 4#80087

Даны функции $f(x)= (x− 6)2− 2,$ $g(x)= x− 2$ и $p(x)= x− 6.$ Графики $f(x)$ и $g(x)$ пересекаются в точках $A$ и $D.$ Графики $f(x)$ и $p(x)$ пересекаются в точках $B$ и $C.$ Найдите площадь четырехугольника $ABCD.$

Показать ответ и решение

Найдём координаты точек пересечения $f(x)$ и $g(x):$

(x− 6)2− 2 = x− 2, 2 x − 13x+ 36= 0. D =132− 4⋅1 ⋅36 = 25 = 52, 13+ 5 13− 5 x1 =--2-- = 9, x2 =--2--= 4.

Тогда

y1(x1)= 9− 2= 7, y2(x2)= 4− 2= 2.

Таким образом, $A (4;2)$ и $D(9;7).$

Найдём координаты точек пересечения $f(x)$ и $p(x):$

(x− 6)2− 2 = x− 6, x2− 13x+ 40= 0. 2 2 D = 13 − 4⋅1⋅40= 9= 3 , x3 = 13+-3 = 8, x4 = 13−-3= 5. 2 2

Тогда

y3(x3)= 8− 6= 2. y4(x4)= 5 − 6 = −1.

Таким образом, $B (5;−1)$ и $C (8;2).$

Рассмотрим рисунок на координатной плоскости:

$PIC$

Найдём площадь фигуры $ABCD$ по формуле Пика ( $B$ — количество точек с целочисленными координатами внутри фигуры, а $Γ$ — количество точек с целочисленными координатами на контуре фигуры):

Γ S = B+ -2 − 1, 10 S = 12+-2 − 1 = 16.

Ответ: 16