03 Газовые процессы в трубках - Каталог заданий по Олимпиадной физике в Школково

Ошибка.
Попробуйте повторить позже

Задача 21#29411Максимум баллов за задание: 10

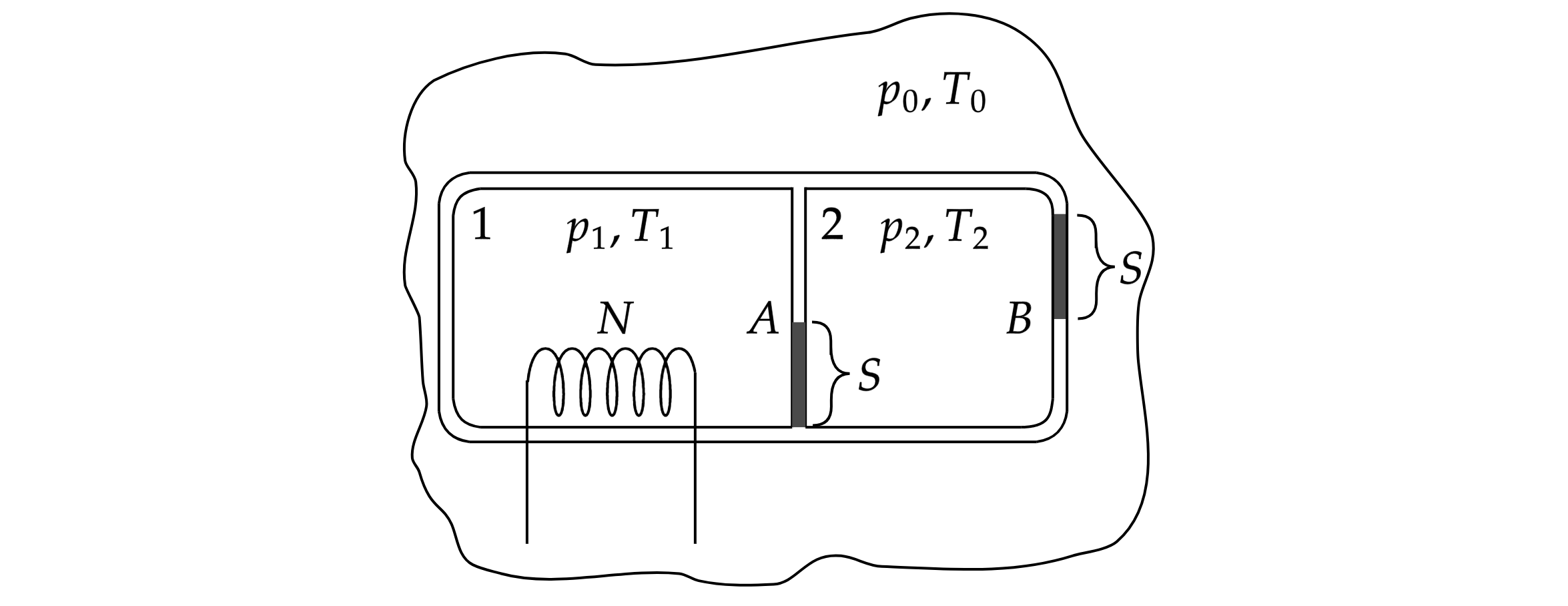
Теплоизолированный сосуд разделён на две части теплонепроницаемой перегородкой A. В перегородке A и в одной из стенок B имеется большое количество маленьких отверстий общей площадью $S$ в каждой. В первой части сосуда включили нагреватель мощности $N$ (рис.). Сосуд заполнен аргоном и помещён в атмосферу аргона. Внешнее давление $p0$ и температура $T0$ поддерживаются неизменными. Оцените установившиеся значения давлений ( $p1$ и $p2$ ) и температур ( $T1$ и $T2$ ) в обеих частях сосуда. Сделайте числовые оценки при $N = 20 В т$ , $S = 10 м м2$ , $p0 = 105 П а$ , $T0 = 300 К$ . Молярная масса аргона $−3 μ = 40 ⋅ 10 кг/м оль$ ; универсальная газовая постоянная $R = 8,3 Д ж/ (моль ⋅ K)$ .

(Всеросс., 1998, финал, 11 )

Источники: Всеросс., 1998, финал, 11

Показать ответ и решение

Среднеквадратичная скорость молекул в газе равна

∘ ----- -- 3kT v = ---- (1) m

Число ударов молекул о стенку сосуда площадью $S$ за единицу времени

dN--= 1nvS, (2) dt 6

где $n$ – концентрация молекул.
В установившемся режиме должно выполняться равенство потоков молекул сквозь перегородку $A$ (и стенку $B$ ). Тогда для перегородки $A$ имеем

1- -- 1- -- 6n1v1S = 6 n2v2S (3)

для стенки $B$ :

1 -- 1 -- -n2v2S = --n0v0S (4) 6 6

Аналогично, мощность переносимая молекулами, уходящими из части 1 сосуда сквозь поры перегородки, равна мощности $P$ нагревателя и мощности, переносимой молекулами приходящими из части 2.

( --2) d- m-v1- 1- -- 3- 1- -- 3- dt N1 2 = 6 n1v1S2 kT1 = P + 6n2 v2S2 kT2 (5)

Решая систему уравнений (3)-(5), получим,

∘ --- p1 = p0 T1-= 1,36 ⋅ 105 П а T0

∘ --- p2 = p0 T2-= 1,09 ⋅ 105 П а T0

( ∘ -----) 4N-- --μ--- T2 = T0 1 + p0S 3RT0 = 354 К

T1 = 2T2 − T0 = 408 К

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 22#29412Максимум баллов за задание: 10

В секции 1 сосуда находится смесь гелия с водородом. Давления водорода и гелия одинаковы, газы разрежены. В секции 2 сосуда вакуум. На короткое время в перегородке открывают маленькое отверстие А. Определите отношение давления гелия к давлению водорода, которое установится в секции 2.

Показать ответ и решение

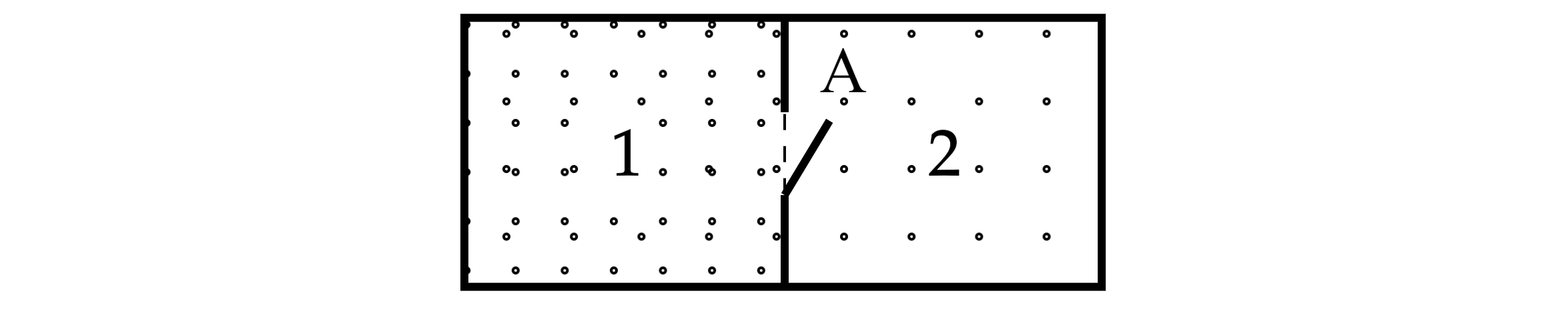
Количество молекул, сталкивающихся с площадкой $S$ , вычисляется по формуле

1- Z = 2nSvx Δt,

где $vx$ – среднее значение модуля проекции скорости на ось X, направленную перпендикулярно площадке.
Таким образом, если $S$ – площадь отверстия, то за промежуток времени $Δt$ из одной части сосуда вылетает $Z0 = 1n0Sv0x Δt 2$ молекул, а влетает $Z = 1nSvx Δt 2$ .
Так как $Z0 = Z$ , то

nH vHx = nHevHex ⇒ nH--= vHex- nHe vHx

Но $vHex$ и $vHx$ – пропорциональны среднеквадратичной скорости молекул, равной

∘ ----- 3kT v = ----, m0

где $m0$ – масса молекулы, а $T$ – температура.
Таким образом,

∘ ---- 1 vHx(vHex) ∼ v ∼ m-- 0

Давление газа в секции

p = nkT

Следовательно,

p n v ∘ m---- √ -- -H--= -H--= -Hx--= --He-= 2 pHe nHe vHex mH

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 23#29413Максимум баллов за задание: 10

В сосуде с воздухом поддерживается температура $T0$ . Температура и давление воздуха вне сосуда равны $T$ и $p$ соответственно. Чему равно давление воздуха внутри сосуда, если в стенке имеется небольшое отверстие? Воздух разрежен.

Показать ответ и решение

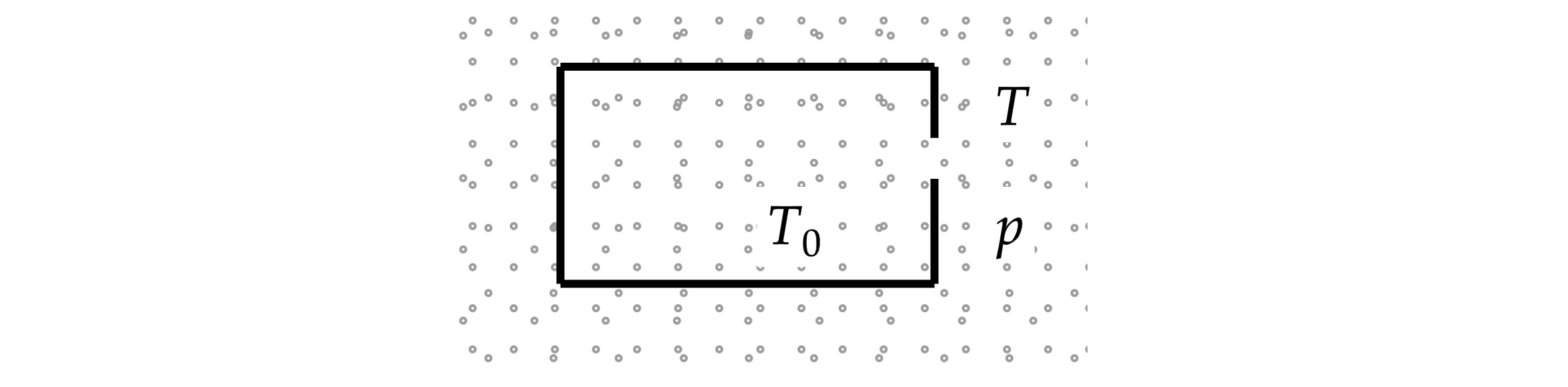
Давление газа $py$ в сосуде можно выразить, используя уравнение, в которое входит концентрация молекул $n0$ . Получаем $py = n0kT0$ . Аналогично давление газа вне сосуда $p = nkT$ , где $n$ – концентрация молекул вне сосуда. Разделив первое равенство на второе, получим

py n0 T0 n0T0 ---= ------⇒ py = p ----- (1) p n T nT

В равновесном состоянии число молекул, влетающих в сосуда за любой промежуток времени $Δt$ , равно числу молекул, вылетающих из этого сосуда. Как было показано при выводе основного уравнения MKT, количество молекул, сталкивающихся с площадкой $S$ , вычисляется по формуле

1 Z = -nSvx Δt, 2

где $vx$ – среднее значение модуля проекции скорости на ось X, направленную перпендикулярно площадке.
Таким образом, если $S$ – площадь отверстия, то за промежуток времени $Δt$ из сосуда вылетает $1- Z0 = 2n0Sv0x Δt$ молекул, а влетает $1- Z = 2nSvx Δt$ . Так как $Z0 = Z$ , то

n v = nv ⇒ n0-= vx- 0 0x x n v0x

Но $v 0x$ и $v x$ – пропорциональны среднеквадратичной скорости молекул, равной

∘ ----- 3kT v = ----, m0

где $m0$ – масса молекулы, а $T$ – температура.
Таким образом,

√ -- v0x(vx) ∼ v ∼ T

Следовательно,

∘ --- vx-= -T- v0x T0

А значит

∘ --- n0 vx T ---= --- = --- n v0x T0

Подставляя отношение концентраций в формулу (1) находим

∘ --- ∘ --- -T-T0- T0- py = p T0 T = p T

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 24#29414Максимум баллов за задание: 10

Два сосуда одинакового объема $V$ соединены узким каналом. В сосудах находится небольшое число частиц $N$ (т.е. частиц так мало, что они почти не сталкиваются друг с другом). Сколько частиц окажется в каждом из сосудов, если температура газа в одном сосуде равна $T 1$ , а во втором – $T2 > T1$ ? В соединительный канал поместили легкий флажок. В какую сторону он отклонится?

Показать ответ и решение

В равновесном состоянии число молекул, влетающих в сосуда за любой промежуток времени $Δt$ , равно числу молекул, вылетающих из этого сосуда. Как было показано при выводе основного уравнения MKT, количество молекул, сталкивающихся с площадкой $S$ , вычисляется по формуле

Z = 1nSv Δt, 2 x

где $vx$ – среднее значение модуля проекции скорости на ось X, направленную перпендикулярно площадке.
Таким образом, если $S$ – площадь отверстия, то за промежуток времени $Δt$ из сосуда вылетает $1 Z0 = -n0Sv0x Δt 2$ молекул, а влетает $1 Z = -nSvx Δt 2$ .
Так как $Z0 = Z$ , то

n1 v2x n1v1x = n2v2x ⇒ ---= --- n2 v1x

Но $v1x$ и $v2x$ – пропорциональны среднеквадратичной скорости молекул, равной

∘ ----- 3kT- v = m0 ,

где $m0$ – масса молекулы, а $T$ – температура.
Таким образом,

√ -- v1x(v2x) ∼ v ∼ T

Следовательно,

∘ --- v2x- T2- v1x = T1

А значит

∘ --- n1-= v2x = T2- n2 v1x T1

Так как концентрации равны

N1 N2 n1 = --- n2 = ---, V V

где $N1$ и $N2$ – искомые величины.
А также $N1 + N2 = N$ , имеем

∘ --- N1 n1 T2 N1 = n1V, N2 = n2V --- = ---= --- N1 n2 T1

Откуда

∘ --- ( √ --- √ --) √ --- N + T1-N = N ⇒ N --T1√-+---T2 = N ⇒ N = N √-----T2√---- 1 T2 1 1 T2 1 T1 + T2

∘ --- √ --- N2 = N1 T1-= N √----T1√--- T2 T1 + T2

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 25#29415Максимум баллов за задание: 10

Оцените подъемную силу пластины площадью $1 м2$ , нижняя поверхность которой находится при температуре $∘ 100 C$ , а верхняя – при температуре $∘ 0 C$ . Температура воздуха $∘ 20 C$ , давление $0,1 П а$ .
Указание: считайте, что в разреженном газе молекулы, уходящие с поверхности твердого тела, имеют среднеквадратичную скорость, соответствующую температуре твердого тела.

Показать ответ и решение

Налетающие на пластину молекулы воздуха имеют среднеквадратичную скорость, равную

∘ ------ -- 3kT0 v = ----, m

где $T0$ – температура воздуха, $m$ – масса молекулы.
Среднее значение абсолютных величин проекций скоростей молекул на ось Oy, перпендикулярную к поверхности пластины, равно

-- ∘ ---- --- -v-- kT0- vy ≈ √3--= m

При столкновении с пластиной "температура"молекул становится равной температуре пластины. Это означает, что после отражения от нижней поверхности пластины

∘ ---- --- kT1 vy′= ---- m

А после отражения от верхней поверхности

∘ ---- v′′= kT2- y m

В результате проекция $py$ импульса молекулы, попадающей на нижнюю поверхность пластины, меняется при соударении на величину

( ∘ ---- ∘ ----) ′ kT0- kT1- Δp y = m m + m

А молекулы, попадающей на верхнюю поверхность, - на величину

( ∘ ---- ∘ ----) ′′ kT0- kT2- Δp y = m m + m

За время $Δt$ на каждую из поверхностей попадают молекулы, находящиеся от пластины на расстоянии, равном $--- vyΔt$ . Число этих молекул равно

--- N = n vySΔt,

где $n$ – число молекул в единице объема, $S$ – площадь пластины.

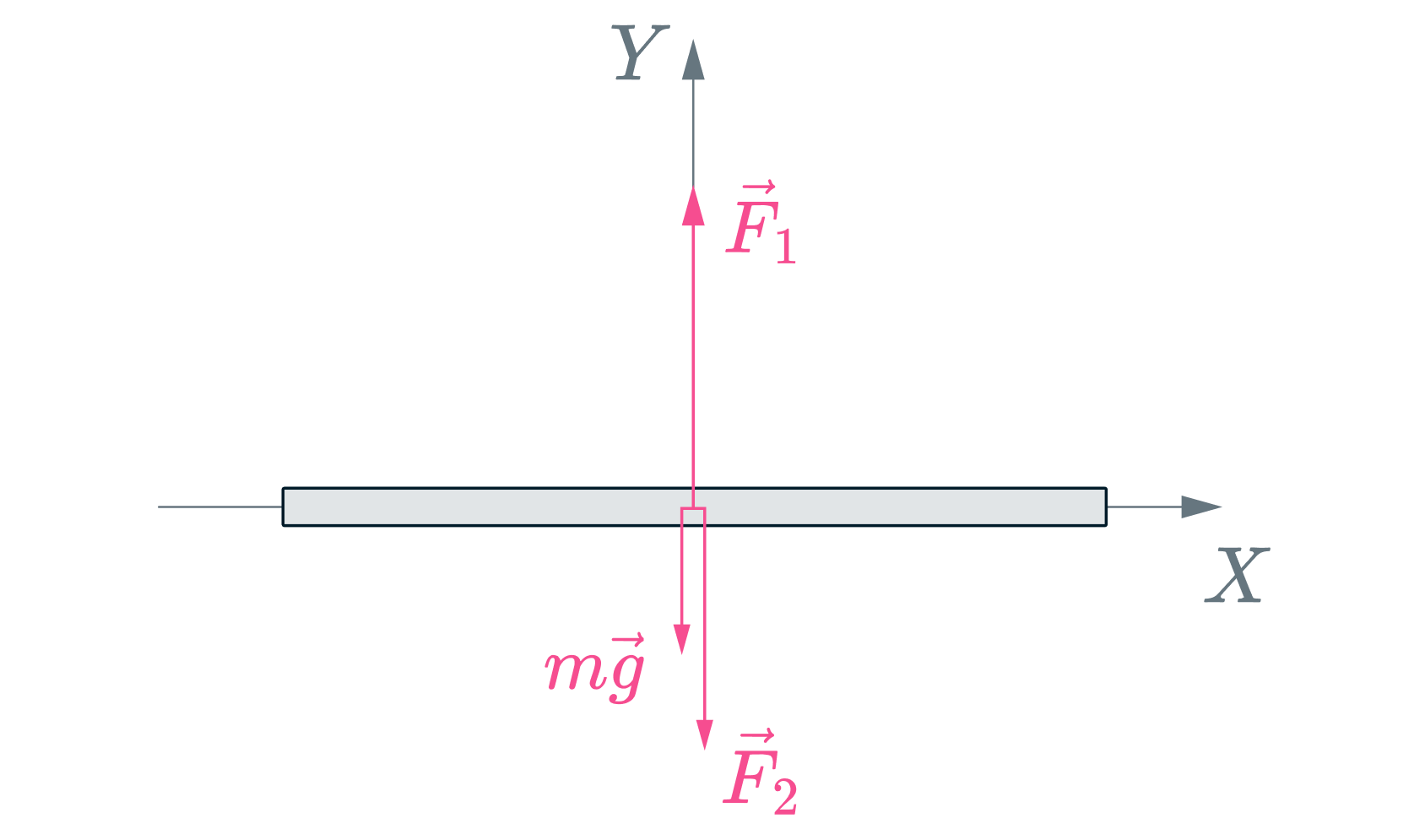
В соответствии со вторым и третьим законами Ньютона на пластину в вертикальном направлении действуют силы, равные по абсолютным величинам изменениям проекций импульсов молекул в единицу времени. На нижнюю поверхность пластины действует направленная вверх сила (рис.)