Тема АЛГЕБРА

Системы уравнений и неравенств

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела алгебра

Разделы подтемы Системы уравнений и неравенств

Арифметические операции над системой

Замены переменных

Оценки в системах

Симметрия или цикличность в системе

Однородные и сводящиеся к ним

Сведение системы к квадратному

Системы неравенств

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#104695Максимум баллов за задание: 7

Решите систему уравнений

(| 1- 1- 4- |||{ x2 + y2 + z2 = 9 | x2+ 9y2 +z2 = 4 |||( √ - √- 2 3x − 6y+ 3z = 2

Источники: ОММО - 2025, номер 5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Обратите внимание на два первых уравнения. Это же просто суммы квадратов каких-то чисел. Почему бы не применить к ним какие-то рассуждения связанные с координатами?

Подсказка 2

Давайте рассмотрим векторы с координатами (1/x, 1/y, 1/z) и (x, 3y, z). Что мы про них знаем, исходя из первых двух уравнений?

Подсказка 3

Очевидно, нам известны их длины. Но также можно посчитать их скалярное произведение. Что можно сказать про их взаимное расположение?

Показать ответ и решение

Первое решение.

Заметим, что в левых частях первых двух уравнений — суммы квадратов. Так можно записать квадраты длин векторов

( 1 1 2) a= x,y,z и b =(x,3y,z).

Согласно условию, $|a|= 3,|b|=2$ . Заметим, что скалярное произведение векторов $a$ и $b$ равно

(a,b)= 1⋅x+ 1 ⋅3y + 1 ⋅z = 6 x y z

что совпадает с $|a|⋅|b|$ , а значит, вектора коллинеарны, причём $a= 3b 2$ . Поэтому

(|| 1 = 3⋅x (|| x =± √√2 { x1 = 29⋅y ⇐⇒ { y =± √32 ||( y2 = 23⋅z ||( z = ± 32√ z 2 3

Подставим эти значения в третье уравнение (выбор знака перед каждым слагаемым независим):

√- √- ±2 2 ∓2 2 ±3= 3

Равенство возможно только в двух случаях: $( √- √- ) √23,32, 2√3$ или $( √- √- ) −√23,− -23 ,√23$ .

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Умножим на 4 и 9 первое и второе равенство в системе соответственно и сложим их:

( ) ( ) ( ) 9x2+ 4- + 81y2 +-4 + 9z2+ 16 = 72 x2 y2 z2

По неравенству о средних получаем, что

(| 2 -4 ||||| 9x + x2 ≥12 |{ 2 4- ||| 81y + y2 ≥ 36 ||||( 2 16 9z + z2 ≥ 24

Тогда

( 2 4 ) ( 2 4) ( 2 16) 9x + x2 + 81y + y2- + 9z +z2 ≥ 72

Следовательно, равенство достигается тогда и только тогда, когда в каждом из неравенств выполняется равенство, то есть

(|| ( 2)2 ||||| 3x − x = 0 ||{ ( 2)2 || 9y − y = 0 ||||| ( )2 ||( 3z − 4 = 0 z

Откуда получаем

- (|| √6- ||||| x =± 3 |{ √2- ||| y =± 3 ||||| 2√3 ( z =± 3

Подставим полученные значения в третье уравнение:

√- √- ±2 2 ∓2 2 ±2= 2

Чтобы избавиться от иррациональности слева необходимо чтобы $x$ и $y$ были одного знака, а равенство превращается в тождество при $2√3- z =--3 .$ Таким образом, получаем 2 решения: $( √6 √2 2√3-) -3 ;-3-;-3$ и $( √6 √2 2√3) −-3-;− -3 ;-3$

Ответ:

$(√6 √2- 2√3) ( √6 √2 2√3) -3 ;-3-;-3 , − -3 ;− 3-;-3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#105456Максимум баллов за задание: 7

Решить систему уравнений

{ x2+ xy+y2 =3 x3+y3 7- x5+y5 = 31

Подсказки к задаче

Подсказка 1

Хотелось бы привести числитель и знаменатель дроби к виду, похожему на первое уравнение!

Подсказка 2

Многочлены x+ y и xy являются простейшими симметрическими многочленами, а любой симметрический многочлен от x и y можно представить в виде многочлена от u и v, где u = x + y, v = xy. Преобразуем числитель и знаменатель дроби, используя это знание)

Подсказка 3

Отлично, теперь нас получилась система относительно u и v! Давайте её преобразуем, чтобы свести к одному уравнению ;)

Подсказка 4

7v² - v - 30 = 0! Осталось лишь разобрать случаи, то есть порешать системы ;)

Показать ответ и решение

Многочлены $x+ y$ и $xy$ являются простейшими симметрическими многочленами, а любой симметрический многочлен от $x$ и $y$ можно представить в виде многочлена от $u$ и $v$ , где $u= x+ y,v = xy$ .

При решении симметрических систем часто приходится выражать через $u$ и $v$ многочлены вида

n n Sn = x + y

Суммы $S ,S ,S ,S 2 3 4 5$ выражаются через $u= x+ y$ и $v = xy$ следующим образом:

S2 =x2 +y2 = u2− 2v 3 3 3 S3 =x +y = u − 3uv S4 =x4 +y4 = u4− 4u2v+ 2v2 S5 =x5 +y5 = u5− 5u3v+ 5uv2

________________________________________________________________________________________________________________________________________________________________________________________________________

Эти формулы можно легко получить самостоятельно. Докажем формулу

Sn = uSn− 1− vSn−2,

позволяющую последовательно выразить через $u$ и $v$ суммы $S3,S4$ , $S5,S6$ и т.д. Для этого заметим, что

( n−1 n−1) n n ( n−2 n−2) uSn−1 = (x+ y)x + y =x +y + xy x + y .

______________________________________________________________________________________________________________________________________________________

Используя формулы, система из условия примет вид

{ u2 = v+ 3 ---u3−3uv-- = 7- u5−5u3v+5uv2 31

Так как $u⁄= 0$ (при $u =0$ второе уравнение системы теряет смысл), то, разделив числитель и знаменатель дроби на $u$ и исключая из системы $u2$ , преобразуем второе уравнение к виду

7v2− v− 30 =0,

откуда $v1 = −2,v2 = 157$ .

Если $v = −2$ , то $u= ±1$ , а если $v = 157$ , то $√- u =± 677$ . Поэтому исходная система равносильна совокупности следующих четырёх систем:

{ x+y =1, { x+ y = −1, xy =− 2; xy = −2; { 6√7- { 6√7 x+y =15- 7 , x+ y =15− 7 , xy = 7 ; xy = 7 .

Первая система имеет решения $(−1;2)$ и $(2;− 1)$ , вторая — решения $(−2;1)$ и $(1;− 2)$ , третья и четвертая системы не имеют действительных решений.

Ответ:

$(−1;2), (2;−1), (−2;1), (1;−2)$

Ошибка.
Попробуйте повторить позже

Задача 3#105457Максимум баллов за задание: 7

Решите систему уравнений

{ 3x2+y2 = 7x2y 2 41 2 2xy− y = 6xy

Подсказки к задаче

Подсказка 1

Работать одновременно с двумя переменными неудобно, так что хотим в перспективе ввести замену. Как можно получить такую замену?

Подсказка 2

Попробуем почленно разделить уравнения из системы. Есть ли какие-то ограничения на это? Если есть, проверяем, являются ли они тоже решениями!

Подсказка 3

Получили новое уравнение с учётом ранее найденных ограничений. Кажется, что здесь уже можно заметить замену. Какую?

Подсказка 4

Введем замену t = x/y. В правой части равенства всё очевидно, а в левой до замены разделим числитель и знаменатель на y². Решаем полученное уравнение.

Подсказка 5

Теперь выполняем обратную замену и, используя изначальную систему, находим значения x и y. При этом не забываем ранее найденные решения, которые не подходят под ограничения после замены!

Показать ответ и решение

Если $x =0$ , то из данной системы получаем, что $y = 0$ , т. е. $(0;0)$ — решение системы.

Пусть $xy ⁄=0$ , тогда разделив уравнения почленно, находим

3x2+ y2 21 x 2xy−-y2-= 2-⋅y

После домножения на знаменатели тут легко можно заметить однородное уравнение, поэтому после надлежащей замены $t= xy$ получаем

2 3t-+-1= 21t 2t− 1 2

простое квадратное уравнение

36t2− 21t− 2= 0, (∗)

которое имеет корни $t1 = 23,t2 =− 112$ .

Заметим, что при $xy ⁄= 0$ полученное уравнение (*) вместе с первым уравнением из условия образует систему, равносильную исходной.

Если $t= 23$ , т. е. $x= 23y$ , то из первого уравнения с учётом условия $x ⁄=0$ получаем $y =3$ и поэтому $x= 2$ .

Если $t=− 112$ , то $y = −12x,x =− 7,y = 84$ .

Ответ:

$(0;0), (2;3), (−7;84)$

Ошибка.
Попробуйте повторить позже

Задача 4#107057Максимум баллов за задание: 7

Для попарно различных вещественных чисел $a,b,c,d,e$ оказалось, что

(| ab+ b= ac+a, |||{ bc+ c= bd+ b, | |||( cd+ d= ce+c, de+ e= da+ d.

Докажите, что $abcde= 1.$

Подсказки к задаче

Подсказка 1

Нам сказали, что числа различны, то есть их разности не 0. Полезно перенести слагаемые в разностях из условия, чтобы возникли разности: например a(b-c)=a-b.

Подсказка 2

Так можно написать 4 выражения. Слева и справа встречаются почти все попарные разности, так что хочется перемножить все эти выражения, но одного не хватает. Где его взять?

Подсказка 3

Для этого можно перемножить все выражения из условия и сократить их! Только стоит не забывать, что делить на 0 нельзя.

Показать доказательство

Пусть какая-то переменная равна $0,$ например, $a.$ Но тогда и $b=0,$ что противоречит условию. Таким образом, все переменные ненулевые. Пусть какая-то переменная равна $− 1,$ например, $a.$ Тогда $c= −1,$ противоречие с условием. Значит, $− 1$ среди переменных тоже нет.

Давайте перемножим все равенства. С учётом рассуждений, описанных выше, мы можем сократить в полученном равенстве одинаковые множители и получить равенство $e(b+ 1)=a(e+ 1).$ Теперь запишем четыре равенства из условия и только что полученное равенство в следующем виде: $a(b− c)= a− b,$ $b(c− d)=b− c,$ $c(d− e)=c− d,$ $d(e − a)= d− e,$ $e(a− b)= e− a.$ Если их перемножить и сократить на одинаковые множители, получим требуемое.

Ошибка.
Попробуйте повторить позже

Задача 5#107202Максимум баллов за задание: 7

На координатной плоскости изображена фигура $Φ(α)$ , состоящая из всех точек, координаты ( $x;y$ ) которых удовлетворяют системе неравенств

{ √- √- (x2− 322 sinα)(y− 3 2cosα)≤0 x + y ≤25

Найдите максимальное значение $M$ периметра (длины границы) фигуры $Φ(α)$ и укажите все значения $α$ , при которых оно достигается.

Источники: Физтех - 2025, 11.6 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Давайте разберёмся, как графически выглядит фигура. Второе неравенство задаёт круг с центром в начале координат и радиусом 5. Чтобы понять, какую область задаёт первое, нужно нарисовать две прямые x = 3√2sin a, y = 3√2cos a и подумать.

Подсказка 2

Итак, в первом неравенстве подойдут области, в которых у скобочек разные знаки. То есть либо область правее первой прямой и ниже второй, либо левее первой и выше второй. Осталось понять, где находится точка пересечения прямых относительно круга и можно делать выводы про область, которую задаёт система?

Подсказка 3

Итак, чтобы найти периметры этих частей круга, нужно отдельно посчитать длины дуг и хорд. Кажется, что длины дуг как-то связаны с углом между хордами, которые из высекают.

Подсказка 4

Для поиска и минимизации суммы длинн отрезков хорд, отсекающий области круга, вам понадобятся координаты точки пересечения прямых и неравенство о средних.

Показать ответ и решение

$PIC$

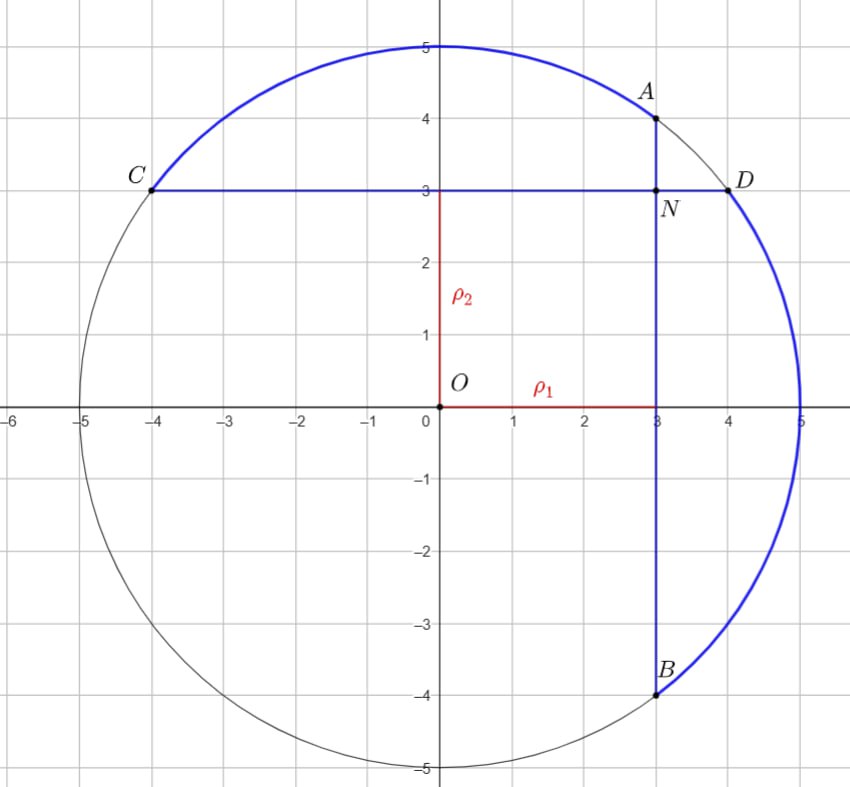
$Φ(α)$ — это две части круга $ω$ с центром в точке $O(0;0)$ и радиуса $R = 5$ , отсекаемые хордами $AB$ и $CD$ , лежащими на прямых с уравнениями $√ - x =3 2sinα$ и $√- y = 3 2cosα$ соответственно. Хорды пересекаются в точке $√ - √- N (3 2sinα;3 2cosα )$ , которая принадлежит $ω$ , так как $√- √ - |ON |2 = (3 2sinα)2+ (3 2cosα)2 = 18 <25 =R2$ . Эта точка $N$ является единственной общей точкой двух частей $Φ(α)$ .

Периметр $Φ (α)$ равен $Σ1+ Σ2$ , где $Σ1$ — сумма длин дуг $AC$ и $BD,Σ2$ — сумма длин хорд $AB$ и $CD$ . Угол между $AB$ и $CD$ равен $π2$ , поэтому

Σ1 = 2⋅ π⋅R = 5π 2

Расстояния от точки $O$ до $AB$ и $CD$ равны $ρ1 =|3√2sinα|$ и $ρ2 = |3√2cosα|$ соответственно, поэтому, используя неравенство $∘ ----- a+2b ≤ a2+2b2$ о среднем квадратическом и среднем арифметическом, получаем

∘R2-− ρ2+ ∘R2-−-ρ2 ∘ --2----√-----2---√------2 Σ24 = ------12-------2-≤ 2R-−-(3-2sinα)2-−-(3-2-cosα)-= 4.

Равенство достигается при

∘R2-−-ρ2-=∘R2-−-ρ2 ⇔ ρ1 = ρ2 ⇔ |sin α|= |cosα| ⇔ |tgα|= 1 ⇔ α = π+ πn,n∈ ℤ 1 1 4 2

Тогда $Σ2 = 16$ , а $M = max(Σ1 +Σ2)= 5π+ 16$ .

Ответ:

$5π+ 16 при α = π+ πn, где n ∈ℤ 4 2$

Ошибка.
Попробуйте повторить позже

Задача 6#116308Максимум баллов за задание: 7

Какие наибольшее и наименьшее значения может принимать произведение двух чисел при условии, что их сумма принадлежит отрезку $[a;b],$ а разность — отрезку $[c;d],$ где числа $a,b,c,d$ положительны?

Показать ответ и решение

Пусть $x$ и $y$ — числа, удовлетворяющие условию задачи, то есть

{ 0< a≤ x+ y ≤ b 0< c≤ x− y ≤d

Так как все числа положительные, можно возвести в квадрат и получим

{ a2 ≤ (x+y)2 ≤ b2 −d2 ≤(x− y)2 ≤ −c2

Откуда имеем

a2 − d2 ≤ (x +y)2− (x − y)2 ≤b2− c2

a2− d2 ≤4xy ≤ b2− c2

2 2 2 2 a-−-d-≤ xy ≤ b-− c 4 4

Наибольшее значение произведения $b2−4c2$ достигается при

{ x+ y = b x− y = c

{ x= b+2c y = b−2c

Аналогично наименьшее значение $2 2 a−4d--$ достигается при $x = a+2d; y = a−2d.$

Ответ:

наибольшее $b2−c2 4$

наименьшее $a2−d2 4$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#119624Максимум баллов за задание: 7

Целые числа $x$ и $y$ связаны уравнением $2x− 3y = 1$ и имеют вид $x= 12a+ b√5,y = ba−1+ 3√5$ для некоторых чисел $a$ и $b.$ Найти $x,y$ и $a,$ если известно, что число $b$ рациональное.

Источники: Росатом - 2025, 11.4 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

В данный момент у нас есть 3 уравнения и 4 переменные. Можно ли как-то уменьшить количество переменных, использую условие?

Подсказка 2

Одно из уравнений — линейное и целочисленное. Давайте выразим его общее решение через некоторую новую переменную (например, t) и будем использовать её вместо х и у.

Подсказка 3

Итак, теперь переменных 3. Давайте посмотрим на два других уравнения. В одном есть слагаемое с a, а в другом с числом, обратным а. Не возникает ли у вас желания перенести эти слагаемые в одну сторону, остальное — в другую и перемножить уравнения? Останется всего лишь две переменные.

Подсказка 4

Теперь давайте вспоминать про рациональность b. Посмотрите внимательно на равенство, которое получилось. В левой части находится выражение вида m + n√5 = h, где m, n, h — рациональные, а вот √5 — не очень рациональный. Какие соотношения для m, n, h должны выполняться, чтобы равенство было верным?

Показать ответ и решение

Общее решение в целых числах уравнения $2x − 3y = 1$ имеет вид $x= 3t− 1$ , $y = 2t− 1$ , где $t$ – целое число. Перепишем уравнения:

{ √- 3t− 1− b√5= 12a− 1 2t− 1− 3 5= ba

Перемножим эти два уравнения:

√ - √- (3t− 1− b 5)(2t− 1− 3 5)= 12b

(3t− 1)(2t− 1)+ 15b− √5(3(3t− 1)+ b(2t− 1))= 12b

Из рациональности $b$ следует, что равенство возможно только если

{ 3(3t− 1)+b(2t− 1)= 0 (3t− 1)(2t− 1)+ 15b= 12b

Выразим $b$ из каждого уравнения:

3(3t−-1) (3t− 1)(2t−-1) b= − 2t− 1 = − 3

(2t− 1)2 =9

[ t= 2 t= −1

Рассмотрим возможные варианты.

Случай 1. $t =2$ :

{ x= 3t− 1= 5 5(1+ √5) y = 2t− 1= 3 ⇒ b=− 5⇒ a= ---12---

Случай 2. $t =− 1$ :

{ √- x= 3t− 1=− 4 ⇒ b= −4 ⇒ a= -5−-1 y = 2t− 1 =− 3 3

Ответ:

$x = 5, y = 3, a = 5(1+-√5); x =− 4, y = −3, a = √5−1 1 1 1 12 2 2 2 3$

Ошибка.
Попробуйте повторить позже

Задача 8#119867Максимум баллов за задание: 7

Найти все пары действительных чисел $a$ и $b,$ удовлетворяющих системе уравнений.

{ a= -6- b= a+5b- 3a−b

Источники: Всесиб-2025, 11.1(см. sesc.nsu.ru)

Подсказки к задаче

Подсказка 1

От знаменателей точно нужно избавляться, но не забудьте про ОДЗ.

Подсказка 2

Равенства получились не очень удобные. Одну переменную через другую не выразить. Зато можно попробовать сложить или вычесть, вдруг получится что-то хорошее?

Показать ответ и решение

Первое уравнение эквивалентно $a2+ ab= 6,$ второе: $3ab− b2 =5.$ Вычтем второе уравнение из первого, получим $a2 − 2ab+ b2 = (a− b)2 = 1,$ откуда $a= b± 1.$

1.: $a =b− 1.$ Подставим в первое уравнение: $2 2b− 3b− 5 =0,$ $−-3±√49 b= 4 .$ Тогда $3 a= 2;−2.$ Обе пары подходят.
2.: $a =b+ 1.$ Подставим в первое уравнение: $2 2b+ 3b− 5 =0,$ $− 3±√49 b= ---4--.$ Тогда $3 a= 2,−2.$ Обе пары подходят.

Ответ:

$±(2,1),±(3,5) 2 2$

Ошибка.
Попробуйте повторить позже

Задача 9#120666Максимум баллов за задание: 7

Найдите все тройки вещественных чисел $x,y,z,$ для которых справедливо равенство множеств:

{ x− y y− z-z-− x} {x,y,z}= y− z ,z− x,x − y

Источники: Курчатов - 2025, 11.6 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Попробуйте рассмотреть, какими могут быть искомые вещественные числа: положительными или отрицательными.

Подсказка 2

Если перемножить xyz в левой части равенства множеств, мы увидим, что оно равно 1, так как равно перемноженной правой части. Тогда попробуйте рассмотреть несколько случаев, связанных с сравнением между собой переменных и 0.

Подсказка 3

Попробуйте составить систему уравнений, руководствуясь сравнением дробей с нулем и друг между друг другом. Попробуйте рассмотреть их числители и знаменатели.

Показать ответ и решение

Заметим, что $xyz = x−-y⋅ y−z⋅ z−x =1, y− z z−x x−y$ поэтому среди чисел $x,$ $y$ и $z$ либо два отрицательных и одно положительное, либо все положительные. Без ограничения общности будем считать, что число $x$ — наибольшее, тогда ясно, что числа $x−y- y−z$ и $y−-z z− x$ имеют разные знаки, значит, $x >0 >y,z.$ Разберем два случая.

Случай 1. $x> 0> y > z$ . В этом случае легко видеть, что $y−z x−-z x−z < x− y$ (числитель меньше числителя, знаменатель больше знаменателя, и все разности положительны). Поэтому $y−z z−-x 0 >z−x > x−y$ и

( |||{ xy − xz =x− y | yz − yx= y− z ||( zx − zy = z− x

Домножая на знаменатели, получаем систему из трех уравнений:

( ||| xy − xz =x− y { yz − yx= y− z |||( zx − zy = z− x

Заметим, что сумма трех этих равенств равна $0,$ поэтому можно рассматривать только первые два. Выражая из второго равенства переменную $y,$ находим $-z--- y = x− z+1.$ Подставляя это выражение в первое равенство и упрощая, получаем:

−1− x − 1 z =--x--, y =1-+x

Когда переменная $x$ будет пробегать все возможные положительные значения, эти две формулы будут описывать соответствующие значения переменных $y$ и $z.$

Заметим, что мы рассматривали случай, когда переменная $x$ — наибольшая. Если придать переменной $x$ отрицательные значения, полученные формулы будут давать ответ в ситуациях, когда наибольшей является переменная $y$ или $z.$ Таким образом, первая серия ответов выглядит следующим образом:

( ) (x,y,z)= t,−--1-,− 1+-t , t∈ℝ ∖{0,−1} t+ 1 t

Случай 2. $x > 0> z > y.$ В этом случае мы получаем аналогичную серию равенств:

x = y− z-, y = x−-y, z = z− x z− x y− z x− y

Домножая на знаменатели, получаем систему из трех уравнений:

( |||{ xz− x2 =y− z | y2− yz = x− y ||( zx − zy = z− x

Складывая эти равенства, получаем формулу $(x− y)(x+ y− 2z)= 0.$ Учитывая, что $x ⁄=y,$ находим $2z = x+ y.$ Тогда $z− x =y − z,$ и первое уравнение нашей системы переписывается в виде $x(z− x)= z− x.$ Вновь вспоминая, что $x⁄= z,$ находим $x =1.$ Остается решить несложную систему:

( {z− yz = z− 1 ( y+ 1= 2z

Решая ее, находим ответ $y = −2$ и $z = − 1 2$ (мы учитываем, что $z >y).$

Вновь циклически переставляя найденные ответы, получаем еще три тройки:

( 1) ( 1 ) ( 1 ) 1,−2,−2 , − 2,1,−2 , −2,−2,1

Ответ:

$(x,y,z)= (t,−-1-,− 1+t), t∈ ℝ∖ {0,−1} t+1 t$

$( 1) ( 1 ) ( 1 ) 1,−2,−2 , − 2,1,−2 , −2,−2,1$

Ошибка.
Попробуйте повторить позже

Задача 10#126183Максимум баллов за задание: 7

Ненулевые числа $x,y,z$ удовлетворяют системе уравнений

(| xy =3z+ z2 { yz =3x+ x2 |( 2 zx =3y+ y

Найдите все возможные значения выражения $(x+ 3)2+ (y+3)2+ (z+ 3)2,$ если известно, что система имеет хотя бы одно решение в ненулевых числах.

Источники: Физтех - 2025, 10.1 ( см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Когда мы видим подобные системы, нередко хочется сложить все уравнения, но пока что не очень понятно, что нам это может дать – всё-таки нам хочется как-то выделить выражения х + 3, у + 3 и z + 3 (или хотя бы выразить квадраты наших переменных), можно ли как-то это сделать?

Подсказка 2

Ага, если преобразовать правые части уравнений, как раз получатся нужные нам скобочки! Но сильно легче от этого не стало, ведь мы даже не можем ничего сократить, в каждом уравнении все еще есть все три переменные :( Давайте тогда получим одно длинное уравнение таким образом, чтобы справа и слева какие-то части можно было сократить.

Подсказка 3

Перемножим наши уравнения, разделим результат на xyz (так как числа ненулевые, мы с чистой совестью можем это сделать), раскроем скобочки и по возможности упростим результат, видим, что в полученном уравнении есть сумма попарных произведений чисел х, у и z, которую очень просто можно выразить через исходную систему, каким образом можно это сделать?

Подсказка 4

Конечно же, просто сложив наши уравнения! Теперь в нашем равенстве есть сумма квадратов и сумма самих переменных, остается понять, что нужно добавить к равенству, чтобы получилось интересующее нас выражение.

Показать ответ и решение

Перемножим левые и правый части уравнений:

2 2 2 xy⋅yz⋅zx =(3z+ z)(3x +x )(3y+ y )

xy⋅yz⋅zx= xyz(3+ z)(3+ x)(3+y)

$x,y,z$ — ненулевые числа. Разделим обе части на $xyz :$

xyz =(x+ 3)(y+ 3)(z+ 3)

Раскроем скобки:

xyz = xyz+ 3xy+ 3xz +3yz+ 9x +9y+ 9z+ 27

(xy +yz+ zx)+3(x+ y+z)= −9

Сложим три уравнения системы:

xy+ yz+xz =3(x+ y+ z)+ x2+ y2 +z2

Подставим в предыдущее равенство:

x2+y2+ z2+ 6(x+ y+ z) =− 9

В итоге получим

2 2 2 2 2 2 (x+ 3) +(y+ 3) + (z +3) = x +y + z + 6(x+ y+ z)+27= 18

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 11#126311Максимум баллов за задание: 7

Найти все тройки действительных чисел $a,b,c$ , удовлетворяющих системе уравнений:

(| ab− c=3 { a+ bc=4 |( 2 2 a + c =5

Источники: Всесиб - 2025, 10.2 ( см. sesc.nsu.ru)

Подсказки к задаче

Подсказка 1

А как обычно решаются системы? Что-то складываем, что-то вычитаем... Есть ли в задаче намёк на то, как и что следует сложить?

Подсказка 2

3² + 4² = 5².

Подсказка 3

Получим, что b = ±2. Рассмотрим оба случая. Вам останется только решить системы с 2 неизвестными.

Показать ответ и решение

Сложим первое и второе уравнения, возведя их в квадрат:

2 2 2 2 (ab− c) + (a +bc) =3 + 4

2 2 2 2 2 2 2 2 2 2 2 a b − 2abc+c + a +2abc+ bc = (b + 1)(a +c )= 3 +4 = 25

Из 3 уравнения знаем, что $a2+ c2 = 5,$ тогда

5(b2+1)= 25

b= ±2

1) $b=2$

Из первого уравнения

c= 2a − 3

Подставим это в третье уравнение:

5a2− 12a+ 4= 0

2 a= 2;5

Имеем 2 кандидата на решение:

a= 2; b= 2; c= 1

2 11 a= 5; b= 2; c=− 5

Первая тройка второму уравнению удовлетворяет, а при подстановке второй во второе уравнение получим в левой части $− 4,$ следовательно, первая тройка является искомым решением.

2) $b=− 2$

Из первого уравнения

c= 2a − 3

Подставим это в третье уравнение:

2 5a + 12a+ 4= 0

a =− 2;− 2 5

Имеем 2 кандидата на решение:

a =− 2; b= −2; c= 1

a= − 2; b= −2; c= − 11 5 5

Вторая тройка второму уравнению удовлетворяет, но, при подстановке первой во второе уравнение, получим в левой части $− 4,$ следовательно, вторая тройка является искомым решением.

Итого получаем

a= 2; b= 2; c= 1

a= − 2; b= −2; c= − 11 5 5

Ответ:

$a =2;b= 2;c= 1$ и $a= 2;b= −2;c=− 11 5 5$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#128581Максимум баллов за задание: 7

Решите систему уравнений

(| 1 ||||| a+ b =1 ||||| b+ 1 =4 { c , |||| c+ 1 =1 ||||| d ||( d+ 1 =4 a

если $a >0,b> 0,c> 0,d> 0$ .

Источники: Звезда - 2025, 10.3 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

У нас уравнения с 4 переменными и обратными к ним, а давайте все перемножим!

Подсказка 2

Система большая, целых 4 уравнения, было бы неудобно как-то их складывать или вычитать. Может, подумаем в сторону неравенств?

Подсказка 3

Воспользуйтесь неравенством о средних.

Подсказка 4

Все неравенства обернулись в равенства. Когда такое может быть?

Показать ответ и решение

Первое решение.

Используем неравенство о средних:

1 ∘ a- 1 ∘ b- 1 ∘c- 1 ∘ d- a+ b ≥2⋅ b, b+ c ≥2 ⋅ c, c+d ≥ 2⋅ d, d+ a ≥ 2⋅ a

Перемножим неравенства:

( ) ( ) ( ) ( ) a + 1 ⋅ b+ 1 ⋅ c + 1 ⋅ d+ 1 ≥24 = 16 b c d a

Из условия, произведение левых частей исходной системы равно $1 ⋅4 ⋅1 ⋅4 =16,$ следовательно, все неравенства превращаются в равенства:

1 1 1 1 a= b, b= c, c= d, d = a

Тогда, после подстановки в изначальную систему, получаем

1 1 a= 2, b= 2, c= 2, d=2

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Вычтем из первого уравнение третье, а из второго четвертое.

( ||{ a− c+ 1− 1= 0 | 1b d1 |( b− d +-c − a = 0

( ||{a− c+ d−-b= 0 | abd− c |(b− d+ -ac-= 0

Из второго уравнения системы выразим

d− b = a− c ac

Подставим в первое:

a− c+ a−-c= 0 abcd

( ) (a− c) 1 +--1- = 0 abcd

Так как $a,b,c,d >0,$ то произведение $abcd$ не может быть равно $− 1.$ Следовательно, $a− c =0,$ то есть $a= c.$ Тогда и $d− b= 0,$ то есть $d= b.$ Получаем систему:

(|| a+ 1= 1 { b ||( b+ 1= 4 a

(||a = b− 1 { b ||(b +--b- =4 b− 1

Решая второе уравнение:

b(b− 1)+ b= 4(b− 1)

b2− 4b+ 4= 0

(b− 2)2 = 0

Следовательно,

1 1 b= 2, d= 2, a= 2, c= 2

Ответ:

$a = 1 ,b= 2,c= 1,d =2 2 2$

Ошибка.
Попробуйте повторить позже

Задача 13#139258Максимум баллов за задание: 7

Решите систему уравнений

{ x3− y3 =7, 2 2 xy − xy = 2.

Показать ответ и решение

Вычтем из первой строчки утроенную вторую, получим что

3 3 x − y − 3xy(x− y)= 1

2 2 (x− y)(x + xy+ y)− 3xy(x− y)= 1

(x− y)(x2 − 2xy+ y2) =1

(x− y)3 = 1

Получили такую систему, которая следствие исходной

{ x− y = 1 xy(x− y)= 2

Сделаем замену $t= −y$ и воспользуемся тем, что $(x − y)= 1$ во второй строчке

{ x+ t=1 xt=− 2

Это теорема Виета для уравнения $2 a − a− 2= 0.$ Его корни $2$ и $− 1,$ делая обратную замену, получаем решения $(2;1)$ и $(− 1;−2).$ После подстановки в исходную систему, получаем что оба решения подходят.

Ответ:

$(2;1)$ и $(−1;− 2)$

Ошибка.
Попробуйте повторить позже

Задача 14#79602Максимум баллов за задание: 7

Про действительные числа $a,b,c$ известно, что

{ ac− 2= 9b2; 3bc− 2= a2

Найдите все значения, чему может быть равно $ab$ .

Подсказки к задаче

Подсказка 1

Во-первых, система не кажется достаточно приятной, чтобы работать с ней в её начальном виде. Как же преобразовать? Свободные коэффициенты и соответствующие коэффициенты перед a и b равны! Значит, надо…

Подсказка 2

Надо вычесть из первого уравнения второе — полученное выражение будет раскладываться на скобки. Достаточно ли нам этого? Давайте проверим, может ли каждая из скобок быть равна 0. Лучше начать с подстановки самой неприятной скобки, ведь вдруг она не может быть равна 0 и с ней не надо разбираться. Чему тогда равно произведение ab, и что может его ограничивать?

Подсказка 3

Одна из скобок не равна 0, а значит, a = 3b, а тогда ab = 3b². Теперь понятно, как ограничено выражение ab. Как тогда понять, достигается ли каждое из предполагаемых нами значений, или же существуют некоторые выколотые точки или даже удалённые интервалы? Верно, предъявить значения параметров, при которых достигается любой элемент из предполагаемого множества значений!

Показать ответ и решение

Вычтем из первого уравнения второе:

c(a− 3b)= (3b− a)(3b+ a)

(a− 3b)(a +3b+ c)= 0

Если $a+ 3b+ c= 0$ , то $a= −3b− c$ и первое уравнение системы

27b2- (3b )2 4 + 2 +c = −2,

не имеет решений. Значит, $a= 3b$ и система сводится к одному уравнению

3bc= 9b2 +2,

которое имеет решение относительно $c$ при всех $b⁄= 0:$

2 c= 9b-+-2 3b

Таким образом, $ab= 3b2 > 0$ , при этом любое положительное значение $d> 0$ произведение $ab$ может принять: достаточно взять

∘ -- d 9b2+2- b = 3,a= 3b,c= 3b

Ответ:

$(0,+ ∞)$

Ошибка.
Попробуйте повторить позже

Задача 15#80763Максимум баллов за задание: 7

Решите систему уравнений

{ √x+-3− √4−-x−-z+5 =2∘y-+-x−-x2-+z; |y+ 1|+ 3|y − 12|=√169-− z2.

Источники: Физтех 2024, 4.2 (olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Первое уравнение выглядит не очень приятным, так что попробуем разобраться со вторым уравнением. Тут у нас ограниченный корень и сумма модулей. Чем можно воспользоваться?

Подсказка 2

Правильно, оценкой. Аккуратно оценим обе части уравнения и подумаем при каких условиях достигается равенство.

Подсказка 3

Отлично, у нас получилась единственная пара (y,z), которую можно подставить в первое уравнение и найти x.

Подсказка 4

Чтобы не возводить в много раз в квадрат уравнение, сделаем замену корней на a и b. Тогда можно записать систему и найти x.

Показать ответ и решение

Рассмотрим второе уравнение системы. Правая часть не больше 13, так как

∘------2 √--- 169− z ≤ 169=13

Попробуем оценить левую часть второго уравнения. Рассмотрим $|y+ 1|+ |y − 12|,$ которое не меньше $13,$ так как $|a|+|b|≥ a+ b,$ где $a =y+ 1, b= 12− y.$ В итоге имеем

|y+ 1|+|y− 12|≥ 13

Прибавим к последнему неравенству $2|y− 12|,$ тогда получим

|y+1|+ 3|y− 12|≥ 13+ 2|y− 12|

Из последнего выражения делаем вывод, что левая часть второго уравнения системы не меньше $13.$ В итоге, получили, что левая часть не меньше $13,$ а правая часть не больше $13.$ Следовательно, чтобы достигалось равенство необходимо, чтобы $y = 12, z = 0.$ Подставим полученные значения $y$ и $z$ в первое уравнения системы для нахождения $x.$

√x+-3− √4−-x−-0+ 5= 2∘12-+-x−-x2+0

---------- √x-+-3− √4-−-x+5 − 2∘ (x +3)(4− x)= 0

Сделаем замену

{ √ ---- a =√-x+-3, a≥ 0, b= 4 − x, b ≥0

Заметим, что $2 2 a + b =7.$ Запишем систему

{ a−2 b+25− 2ab= 0 a + b =7

(| b−-5- ||{ a= 1− 2b || ( )2 |( 1b−− 52b + b2 =74x4− 4x3− 26x2+18x+ 18

4 3 2 4b-− 4b-−-26b-+2-18b-+18= 0 (1 − 2b)

Рассмотрим, когда числитель становится равным 0

4b4− 4b3− 26b2+18b+ 18 =0 ⇐ ⇒ 2(b2+b− 3)(2b2− 4b− 3)=0

Из последнего уравнения получаем совокупность решений

√-- ⌊ b= −1±--13- || 2 |⌈ 2± √10 b= --2---

С учетом ограничений получаем следующие $b$

⌊ √-- b= −1+--13- ||| 2 ⌈ 2+-√10 b= 2

Тогда сделаем обратную замену

⌊ √-- √4-− x-=-13−-1 ||| 2 ⌈ √ ---- 2+√10- 4− x = 2

⌊ √-- √-- | x= 4− 7−2-13= 1+-213 ||⌈ √-- √-- x= 4− 7+-2-10= 1−-2-10 2 2

Ответ:

$(1+ √13 ) (1− 2√10 ) ---2--;12;0 , ---2---;12;0$

Ошибка.
Попробуйте повторить позже

Задача 16#81371Максимум баллов за задание: 7

Каким наибольшим может быть значение выражения $A +B$ , если $A$ и $B$ – числа, удовлетворяющие следующей системе неравенств

( 3A +5B ≤11 |{ |( 4A +3B ≤10 7A +4B ≤18

Источники: Миссия выполнима - 2024, 11.2 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Давайте для начала поймём, что нам неудобно работать с величинами A и B. Так как нам нужно максимизировать не их, а их сумму (это не всегда одно и то же, если мы максимизируем каждое по отдельности, у нас может получиться оценка, которая не достигается), то давайте обозначим за S = A + B сумму этих чисел и заменим везде в неравенствах, чтобы в них фигурировало только S и A (система с тремя переменная - это совсем грустно). Тогда чтобы решить задачу, нам остаётся дать оценку на A снизу через S, так как тогда два вторых получившихся неравенства дадут нам выбор из минимумов

Подсказка 2

Подставляя оценку A >= (5S - 11) / 2. в два оставшихся неравенства, у нас получается оценка на S сверху. Значит, остаётся выбрать то, что даёт минимальную. И всё?

Подсказка 3

Конечно, нет. Нам нужно привести пример. Однако здесь, чтобы привести пример, достаточно просто «развернуть» наши действия, посмотреть в какой точке достигается равенство и так найти, чему должно быть равно А.

Показать ответ и решение

Обозначим за $S =A +B$ , тогда систему можно переписать в виде:

( 5S − 2A ≤11 |{ |( 3S +A ≤10 4S +3A ≤18

Представим первое неравенство, как $A ≥ 5S−11, 2$ тогда получаем

(| 5S−-11-≤A { 11S2−11≤ 3S+ A≤ 10 |( 23S2−33≤ 4S+ 3A≤ 18 2

Откуда получаем оценку

( ) S ≤min 2⋅10-+11,18⋅2+-33- = 31 11 23 11

При этом равенство достигается в точке области

17 14 A= 11,B =11

(являющейся точкой пересечения прямых $3A +5B = 11,4A+ 3B =10$ ).

Ответ:

$31 11$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#82780Максимум баллов за задание: 7

Решите систему уравнений

{ (xy+ 3x− y − 3)|y− x− 9|=(x− 4)|xy+3x − y− 3|; √y-−-x+9-=y − 4.

Источники: Ломоносов - 2024, 11.3 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Надо понять, какие есть возможности выполнения 1-го уравнения. Имеется одинаковая скобка справа и слева, на неё можно сократить (не забывая про модуль), когда она не равна нулю. Следовательно, можно отдельно рассмотреть случаи равенства и неравенства нулю этой скобки, также не забывая про ОДЗ.

Подсказка 2

Когда ни одна из скобок первого уравнения не равна нулю, учесть модули можно довольно просто — их наличие равносильно тому, что произведение всех скобок без модулей положительно (поскольку, если оставить все модули в одной стороне, а скобки без модулей перенести в другую, то дробь без модулей обязана быть положительной). Далее уже сложностей не остается — нужно лишь аккуратно поделить всё на случаи и довести их до конца, учитывая ОДЗ.

Показать ответ и решение

Из второго уравнения следует, что $y ≥ 4$ , так как корень неотрицателен.

Пусть первое уравнение выполняется из-за того, что $(xy+ 3x − y− 3)= 0$ . Условие равносильно $(x− 1)(y +3)= 0$ . Решение $y = −3$ не подходит, а при $x= 1$ получаем:

({ ∘y+-8= y− 4 ⇐⇒ y ≥ 4, ⇐⇒ y = 8 (y2− 9y+8 =0.

Пусть теперь $(xy +3x− y− 3)⁄=0$ , но $(x− 4)= 0$ , и $(y − x − 9)= 0$ . Тогда $x= 4,y = 13$ , но такой вариант не подходит под второе уравнение.

При остальных $x,y$ система равносильна системе:

( ( |||{ (x − 1)(y +3)(x − 4)> 0, |||{(x− 1)(y+ 3)(x− 4)>0, y− x− 9= ±(x − 4), ⇐⇒ y =13 или y = 2x+ 5, |||( √y−-x+-9= y− 4 |||(√y-−-x+-9= y− 4

При $y = 13$ решением будет $x= −59$ , при $y = 2x+ 5$ получим уравнение:

√----- ({ x≥ 0.5, x+ 14= 2x +1 ⇐ ⇒ ( 2 4x +3x− 13= 0

Откуда $−3+√217- x= 8$ , тогда $17+√217- y = 4$ . Последняя пара не удовлетворяет условию $(x − 1)(y +3)(x − 4)> 0$ .

Ответ:

$(1,8),(−59,13)$

Ошибка.
Попробуйте повторить позже

Задача 18#88246Максимум баллов за задание: 7

Решите систему

{ 6x − 2⋅3y = 2; 6x ⋅3y =12.

Показать ответ и решение

Обозначим $6x = a, 3y = b$ . Тогда

{ a− 2⋅b=2 a⋅b= 12

Выразив $a= 2+2b$ и подставив во второе уравнение, получим

b(2 +b)= 12 ⇐ ⇒ (b− 2)(b+3)= 0

Причем $b= −3$ не подходит, так как $b= 3y > 0$ . Итого, $b= 2, a= 6$ . Делая обратную замену, получаем $6x = 6, 3y = 2 =⇒ x =1, y = log32$

Ответ:

$(1,log 3) 2$

Ошибка.
Попробуйте повторить позже

Задача 19#92117Максимум баллов за задание: 7

Найдите все тройки положительных чисел $x,y,z$ удовлетворяющие системе уравнений

{ (x2+ xy +y2)(y2+yz+ z2)(z2+ zx+ x2) =xyz (x4+ x2y2+ y4) (y4+ y2z2+ z4)(z4+ z2x2+x4)= x3y3z3

Источники: ДВИ - 2024, вариант 243, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Уравнения в системе довольно схожие, правая часть второго делится на правую часть первого. А можно ли что-то такое отметить и для левых частей?

Подсказка 2

Попробуйте разделить второе уравнение на первое!

Подсказка 3

(x⁴ + x²y²+ y⁴) = (x² + xy + y²)(x²- xy + y²)

Подсказка 4

Теперь мы умеем представлять x²y²z² в виде произведения трёх скобок. Давайте подумаем, а на что похожи выражения в скобках? Как можно оценить каждую из них?

Подсказка 5

Вспомните, что a² + b² ≥ 2ab!

Показать ответ и решение

Поделим второе уравнение на первое (так как обе части первого уравнения положительны). Отношение первых скобок равно

x4+x2y2+ y4 (x4+ x2y2+y4)(x2− y2) x2-+xy+-y2-= (x2-+xy+-y2)(x−-y)(x+-y) =

6 6 = ---x-−-y----= x2− xy+y2 (x +y)(x3− y3)

Аналогичное равенство имеет место для второй и третьей скобок, тогда после деления получим:

( 2 2) (2 2) ( 2 2) 2 22 x − xy +y ⋅ y − yz+ z ⋅ z − zx +x = x yz

С учетом того, что $a2+ b2 ≥2ab, ∀a,b ∈ℝ$ и того, что все числа положительные (тогда мы можем перемножать неравенства), получим:

2 22 ( 2 2) ( 2 2) (2 2) x y z = x − xy+ y ⋅ y − yz+ z ⋅z − zx+ x ≥

≥ xy⋅yz⋅zx= x2y2z2

А значит, наше равенство выполняется только в случае $a2 +b2 = 2ab,$ то есть в случае равенства всех переменных. Тогда подставляя $y =x,z = x$ в первое уравнение, получим