Системы уравнений и неравенств

Функция двух переменных и называется симметрической, если . В системах уравнений, содержащих симметрические функции, часто удобнее решать относительно переменных и .

Выразим через :

Тогда изначальная система в будет выглядеть:

Подставим второе уравнение в первое:

Единственный корень . Тогда .

Остаётся решить систему

Подставляя первое уравнение во второе, получаем , откуда выходит два решения:

Вычтем из первого уравнения второе:

Случай 1:

Подставляем в : . Тогда получаем два решения:

Прямая подстановка в условие показывает, что оба решения подходят.

Случай 2:

Подставляем в :

Так как , то здесь нет решений.

Функция двух переменных и называется однородным многочленом второй степени, если она имеет вид Для решения системы из однородных уравнений надо сложить уравнения с такими коэффициентами, чтобы получить в правой части 0.

Сразу отметим, что

Запишем уравнение :

Заменим на получим:

Случай 1:

Перепишем Откуда получаем два решения:

Прямая подстановка в условие показывает, что оба решения подходят.

Случай 2:

Перепишем Откуда получаем два решения:

Прямая подстановка в условие показывает, что и эти решения подходят.

Поделим первое уравнение на второе

Теперь перемножим уравнения исходной системы

Воспользуемся, что

Тогда

Проверив, получаем, что решение —

Заметим, что Домножим второе уравнение на

Теперь подставим первое равенство во второе

Рассмотрим два случая:

1) Пусть тогда

Проверив, получаем, что — решение.

2) Пусть тогда

При

Значит, такого быть не может. При

Проверив, получаем, что — решения.

Подставим второе уравнение в первое

Сделаем замену тогда

Теперь сделаем обратную замену

В итоге получаем решения

Данная система неравенств эквивалентна следующим:

Первое неравенство задаёт полосу между параллельными прямыми и а второе — полосу между прямыми и Их пересечением является параллелограмм. Найдем его вершины, решив соответствующие системы линейных уравнений:

Аналогичным образом находим, что параллелограмм имеет вершины в точках

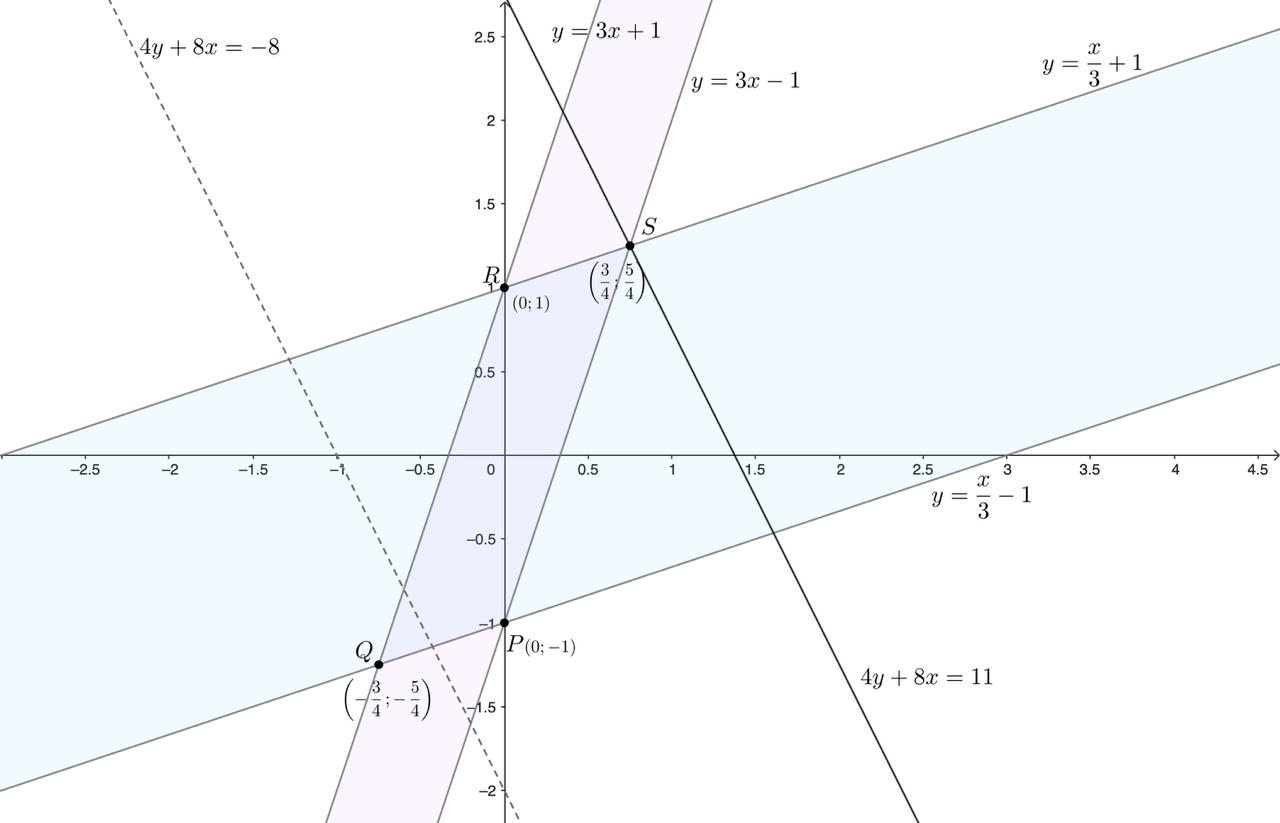
Рассмотрим уравнение где — некоторая константа. Оно задаёт прямую на плоскости, причём в любой точке прямой значение выражения постоянно и равно Если изменить значение получится некоторая другая прямая, на которой выражение принимает новое значение. Нам необходимо определить максимальное значение при котором прямая пересекает параллелограмм. Несложно увидеть, что при увеличении прямая движется вверх на плоскости, и самое большое получается, когда прямая проходит через точку Это значение равно:

Запишем второе уравнение системы в виде

Введем функцию

Теперь можем переписать это уравнение в виде Функция строго возрастает на всей своей области определения, как сумма трёх возрастающих при функций. Отсюда следует, что каждое своё значение она принимает единственный раз. Значит, Подставляя в первое уравнение, получаем

Обозначим Возводя обе части в квадрат, получаем

Отсюда

Уравнение принимает вид

Значит,

Если то

Возведя в квадрат обе части и упростив, получаем:

Это уравнение равносильно системе:

Подходит только корень

Если то

Левая часть этого уравнения — возрастающая функция, а правая — убывающая. Из второго уравнения следует, что Значит, минимальное значение левой части равно а максимальное значение правой — (оба значения принимаются при Следовательно, в этом случае решений нет. Итак, система имеет единственное решение

Умножим обе части системы на

Вычтем из первого уравнение второе

Откуда или или Этим двум случаем соответствуют решения или

Несмотря на то, что при виде условия хочется плакать, можно домножить первое уравнение на , второе на и сложить все три уравнения, чтобы избавиться от и выделить

В первом случае получаем систему

В зависимости от знака оно принимает значения , откуда и получаем второе уравнение. Рассмотрим оба случая

• . Но тогда левая часть неотрицательная, а правая — отрицательна, решений нет.
• . Получаем решение , далее сократим на скобку , получим . Заметим, что в левой части монотонная функция, поэтому решений не более одного. Нетрудно угадать, что подойдёт только .

Итак, , при этом (нам подошёл второй случай), откуда .

Вернёмся к случаю . Отсюда получаем

Из первого уравнения , подставляем

• , в этом случае решений нет.
• , здесь . Отсюда сразу же находим . Наконец, найдём .

Заметим, что

Тогда для каждого имеем откуда

Окончательно получим

Значит, для каждого выполнено

откуда

Отсюда несложно получаем, что тогда один из равен а все остальные равны

Разложим каждое уравнение в произведение скобок

Решение последней системы:

Первое решение.

Если тройка является решением, то решениями являются . В силу этой цикличности системы мы можем не умаляя общности считать наибольшим.

Вычтем из первого уравнения второе и третье:

Если то поэтому должно достигаться равенство

Если то поэтому должно достигаться равенство

Таким образом, система может иметь решение только при При подстановке в любое из уравнений системы получаем

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Заметим, что в любой тройке, являющейся решением, все переменные одного знака: они либо все неотрицательны, либо все неположительны. Это следует из того, что нечётная степень числа имеет тот же знак, что и само число. Действительно, среди переменных две имеют одинаковый знак, тогда правая часть уравнения, содержащего эти переменные, имеет тот же знак, значит и левая часть, а с ней и третья переменная имеют тот же знак. Кроме того, если одна из переменных равна то левая часть соответствующего уравнения равна значит сумма двух чисел одного знака в правой части тоже равна поэтому каждое из этих чисел равно

Внесём эту тройку в ответ. Тогда дальше можно считать, что все переменные не равны При умножении решения системы на снова получаем решение, следовательно, дальше можно считать, что а потом внести в ответ тройку с противоположными знаками.

Сложим все три уравнения и перенесем правую часть в левую:

Теперь рассмотрим функцию Нетрудно понять, что при значении функции отрицательно, а при положительно, а также при оно равно Отсюда следует, что все переменные не могут быть одновременно больше или одновременно меньше Так как иначе ведь в левой части стоит сумма трёх чисел одного знака, поэтому они все должны равняться откуда следует, что при этом

Итак, остались два случая, и

Если тогда — это не решение.

Если — это тоже не решение.

Таким образом доказано, что других решений, кроме уже найденных, нет.

При условии того, что обе переменные не равны нулю, имеем:

Значит:

Пусть

Тогда получим:

Докажем, что наибольший корень реализуется. Действительно, из обоих уравнений получаем подставляя Они подходят, так как наши преобразования были равносильны с учетом того, что

Домножим второе уравнение на и сложим с первым, тогда получим:

Тогда из последнего уравнения следует, что Проверяем полученный ответ:

Вычтем последнее уравнение системы из первого:

По условию все числа различны, значит скобка не равна нулю. Отсюда то есть Получается, наша система равносильна следующей:

Так как числа и положительны, то Тогда

Прибавим к первому уравнению два других и выделим полные квадраты по каждой переменной:

Следовательно, единственное возможное решение. Проверим это подстановкой в уравнения системы:

Вычтем из первого уравнения второе и получим равносильную систему:

В итоге получаем две пары и пишем ответ.

Эту задачу легче всего решат те, кто хорошо знает формулу квадрата суммы трех чисел: . При этом ее надо узнавать справа налево, т.е. сложить все три уравнения системы, раскрыть скобки и убедиться, что слева стоит полный квадрат выражения .

Справа будет число . Отсюда имеем два случая: и

1) . Применим формулу разности квадратов к каждому из уравнений системы. Получим, что

Подставив вместо число , будем иметь простую систему

которая легко решается: .

2) . Этот случай разбирается в точности так же, как и предыдущий, с заменой соответствующих знаков на минусы.

Сложим уравнения:

Осталось проверить решения, подставив их в первое уравнение, откуда получаем ответ.