Тема АЛГЕБРА

Системы уравнений и неравенств

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела алгебра

Разделы подтемы Системы уравнений и неравенств

Арифметические операции над системой

Замены переменных

Оценки в системах

Симметрия или цикличность в системе

Однородные и сводящиеся к ним

Сведение системы к квадратному

Системы неравенств

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 81#96524Максимум баллов за задание: 7

Напряжённость электрического поля в точке $(x,y)$ описывается функцией

( )x2+y2 E(x,y)= 2201 .

Найдите максимальное значение напряжённости в области, задаваемой неравенствами

|ax+ y|≤b, |ax− y|≥ b,

где $a$ и $b$ — фиксированные вещественные числа.

Подсказки к задаче

Подсказка 1

Рассмотрим f(x, y) = x² + y². Как эта величина связана со значениями E(x, y)? Как выразить отсюда максимум E?

Подсказка 2

Правильно, нам необходимо найти минимум f(x, y) в области из условия. Для этого рассмотрим различные значения a и b. На какие части можно условно разделить эту подзадачу?

Подсказка 3

Случай b < 0 очевиден, как и b = 0. В случае b > 0 рассматриваем возможные значения a, представляем полученные ограничения на плоскости. Можно подумать, что в этом случае задает f, какие фигуры/расстояния нам нужно найти и из этого выражать минимум.

Показать ответ и решение

Функция $E (f)= (20)f 21$ монотонно убывает при $f ∈ [0,∞ ).$ Рассмотрим величину $f(x,y)= x2+ y2,$ если переменные удовлетворяют неравенствам

|ax+ y|≤b, |ax− y|≥ b.

Максимум $E$ соответствует минимуму $f.$

1. Если $b <0$ , то множество решений системы неравенств пусто. Функция не определена.

2. Если $b =0$ , то неравенства равносильны уравнению $ax +y = 0$ , откуда $f(x,− ax)= g(x) =(1+ a2)x2$ . Максимум $E(x,y)$ будет достигаться в начале координат и будет равен $1.$

3. Пусть $b> 0,a= 0.$ Тогда система неравенств равносильна уравнению $|y|= b$ и $2 2 2 f(x,y)= f(x,|b|)=x +b ≥ b.$ Максимум равен $(20)b2 21 .$

4. Пусть $b> 0,a> 0.$ Тогда получаем систему ограничений

−b− ax ≤y ≤b− ax, (y ≤ ax− b или y ≥ ax+ b).

Она задает на плоскости область между двумя параллельными прямыми $y = −b− ax$ и $y = b− ax$ и вне ромба с вершинами $(0;±b),(±b∕a;0).$ Функция $f$ есть квадрат расстояния от начала координат до точки области. Точки с одинаковым расстоянием от $O$ образуют окружность. Минимум расстояния имеют точки касания сторон ромба со вписанной в ромб окружностью. Найдем ее радиус $r.$

$PIC$

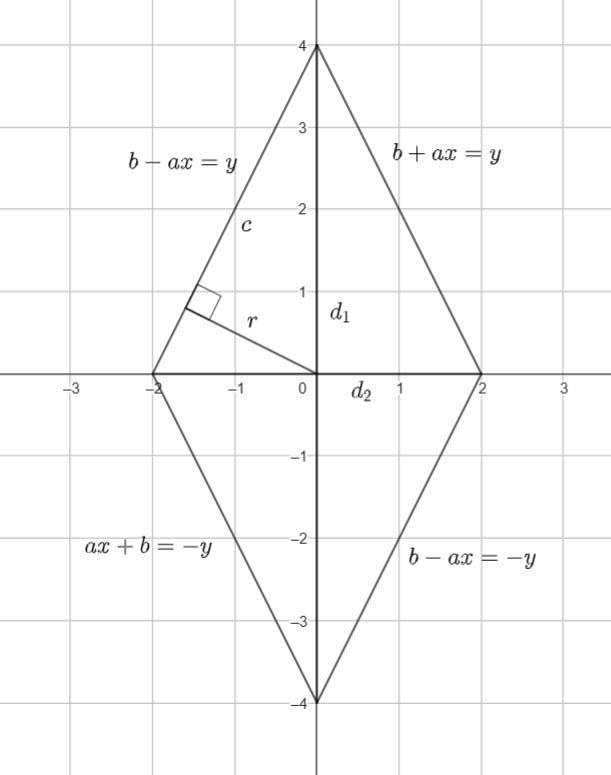
Рассмотрим площадь ромба $S =d1d2∕2.$ Его диагонали имеют длины $d1 =$ $2b∕a,d2 = 2b,S = 2b2∕a,$ сторона $− c= ∘b2-+(b∕a)2 = b√a2-+1∕a.$

Рассмотрим площадь прямоугольного треугольника с катетами $b∕a,b,$ составляющего четверть ромба:

SΔ = S∕4 =b2∕(2a)= (1∕2)cr= b∘a2+-1∕(2a)

Отсюда

--b--- 2 -b2-- r = √a2+-1, fmin = r = a2+1

5. Случай $b >0,a< 0$ аналогичен предыдущему и приводит к такому же результату.

Объединяя результаты $3 − 5$ , получаем короткий ответ.

Если $b< 0,$ то функция $f$ не определена. Если $b≥ 0,$ то

2 E =( 20)ab2+1 max 21

Ответ:

$(20)ab22+1 21$ при $b ≥0$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 82#31169Максимум баллов за задание: 7

Решите систему уравнений

{ xy − z2 = 9, x2 +y2+ z2 = 18.

Источники: по мотивам ОММО - 2020

Подсказки к задаче

Подсказка

Три неизвестные в двух уравнениях - плохо. Или наоборот хорошо? Можно не решать алгебраически, а смухлевать заменой: используйте первое уравнение и оценку на сумму квадратов во втором неравенством о средних

Показать ответ и решение

Система равносильна

{ 2xy = 18+ 2z2, x2 +y2 = 18− z2.

Так как $x2+ y2 ≥ 2xy$ , то

18− z2 ≥18+ 2z2 =⇒ z2 ≤ 0=⇒ z = 0

В итоге получим систему

( |{ z = 0; | x2+ y2 =2xy; ( xy = 9.

То есть $x= y = ±3,z =0,$ откуда и получаем ответ.

Ответ:

$(−3,−3,0),(3,3,0)$

Ошибка.
Попробуйте повторить позже

Задача 83#31185Максимум баллов за задание: 7

Решите систему

({ ∘ x- ∘-y -7- √y + x = √xy√ +-1; ( x xy+ 78= −y xy.

Источники: ПВГ-2020

Подсказки к задаче

Подсказка 1

Перенеся во втором уравнении правую часть налево, а 78 - направо, подумаем, что нужно сделать, чтобы сверху тоже получилось это выражение.

Подсказка 2

Конечно, напрашивается умножить на ху первое уравнение, только нужно рассмотреть два случая: когда 1) x>0 y>0 или 2) x<0 y<0, чтобы верно произвести умножение с корнями

Подсказка 3

Важно подметить, что в 1 случае sqrt(х^2) будет равен х, а во втором этот же корень равен -х. Эти два случая приведут к квадратным уравнениям относительно t = sqrt(xy), к решениям которых мы потом применим обратную замену и найдем ответ.

Показать ответ и решение

Область определения системы распадается на две подобласти: $1) x,y > 0$ и $2) x,y < 0$ .

При умножении первого уравнения на $xy ⁄= 0$ , получаем

∘ x- ∘ y- √-- x⋅(y⋅ y)+ y⋅(x⋅ x)= 7 xy+ xy

В подобласти $(1)$ верно $∘-- √-- y = y2,x = x2$ , то есть мы можем занести под корень и сократить:

{ √-- √-- √-- x xy+ y-xy =7 xy +xy x√xy+ 78= −y√xy

откуда следует, что число $√ -- t= xy$ удовлетворяет квадратному уравнению $t2 +7t+ 78 =0$ , которое решение не имеет.

В подобласти $(2)$ же из-за того, что $∘ -- √ -- y = − y2,x= − x2$ при занесении под корень в левой части появляются минусы перед корнями:

{ √ -- √ -- √ -- − x xy−√y-xy = 7 xy+√ xy; x xy +78= −y xy,

откуда следует, что число $√ -- t = xy$ удовлетворяет квадратному уравнению $2 t +7t− 78 =0$ , решениями которого являются $t1 = −13,t2 = 6$ .

Так как $t> 0$ , то с учетом исходной системы получаем $x⋅y =36,x+y = −13.$ В итоге имеем две пары решений $(− 9;−4),(−4;−9)$ .

Ответ:

$(−9;−4),(−4;−9)$

Ошибка.
Попробуйте повторить позже

Задача 84#33593Максимум баллов за задание: 7

Найдите количество пар целых чисел $(x,y)$ , удовлетворяющих системе неравенств

{ y > 2x+ 3⋅265 y ≤ 70+(264− 1)x

Ответ должен быть представлен в виде алгебраической суммы не более двух слагаемых.

Источники: Физтех - 2020, 11.7 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Так как мы хотим "зажать" y между двумя графиками, имеет смысл порассуждать об их точках пересечений и о том, как графики выглядят.

Подсказка 2

Один из графиков выпуклый вниз, а другой — линейный. Сколько у таких графиков точек пересечений? Попробуем их подобрать ;)

Подсказка 3

У графиков ровно две точки пересечения, абсциссы у них — 6 и 70. Тогда где находятся нужные нам значения y?

Подсказка 4

Нам нужны целочисленные точки, которые лежат "между графиками". Попробуем тогда посчитать целочисленные точки под каждым из графиков (и над осью x), а затем подумать, как же связаны эти величины с ответом!

Показать ответ и решение

Пусть $f(x)=2x +3⋅265,g(x)=70+ (264− 1)x$ . В силу того, что $f(x)$ выпукла вниз, а $g(x)$ - линейная, графики функций $f(x)$ и $g(x)$ могут иметь не более двух общих точек (достаточно взять вторую производную разности). Координаты обеих точек легко подобрать. Действительно, $6 65 64 ( 64 ) f(6)=2 + 3⋅2 =64+ 6⋅2 =70+ 2 − 1 6= g(6)$ и $70 65 6 64 64 (64 ) f(70)= 2 + 3⋅2 =2 ⋅2 + 6⋅2 = 70+ 2 − 170= g(70)$ . На промежутке $6< x< 70$ график $f(x)$ лежит ниже графика $g(x)$ . Поэтому система имеет целочисленные решения только при целых $x∈ [7;69]$ (так как первое неравенство системы строгое, точки пересечения графиков не являются решениями системы).

Заметим, что на отрезке $[7;69]$ графики функций $f(x)$ и $g(x)$ лежат выше оси $x$ . Поэтому искомое количество целочисленных точек мы получим, если из количества $S1$ целочисленных точек с неотрицательными ординатами, лежащих под графиком $g(x)$ на отрезке $[7;69]$ , вычтем количество $S2$ целочисленных точек с неотрицательными ординатами, лежащих под графиком $f(x)$ на отрезке $[7;69]$ . При этом мы учтём, что первое неравенство системы строгое, а второе — нет.

Найдём $S1$ . Так как на отрезке $[7;69]$ лежат $69− 7+ 1= 63$ целочисленные точки, то

( ) ( ) S1 =70⋅63+ 264− 1 (7+ 8+ ...+ 69)= 70⋅63+ 264− 1⋅38⋅63=

= 32⋅63+ 264⋅38⋅63= 2016+ 265⋅1197

Найдём $S2 :$

( 7 65) (8 65) (69 65) S2 = 2 + 3⋅2 + 2 + 3⋅2 + ...+ 2 + 3⋅2 =

7 8 69 65 70 7 65 5 65 65 65 = 2 +2 + ...+ 2 + 3⋅2 ⋅63= 2 − 2 + 3⋅2 ⋅63 =2 ⋅2 − 128+ 189⋅2 = 221 ⋅2 − 128

Искомое количество равно

S1− S2 = 2016+ 265⋅1197− (221⋅265 − 128)=

= 2144+ (1197− 221)⋅265 =2144+ 976⋅265 = 2144+ 61⋅269

Ответ:

$61⋅269+2144$

Ошибка.
Попробуйте повторить позже

Задача 85#77810Максимум баллов за задание: 7

Решите систему уравнений

{ 12x2+ 4xy+ 3y2+ 16x= −6 4x2 − 12xy+ y2 +12x− 10y =− 7

Источники: ОММО - 2020, номер 5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Видим, что уравнения представляют из себя многочлены степени 2 от двух переменных и не понимаем, что с ними делать. Самое простое и приятное - попытаться выделить полные квадраты. Нам дана система, поэтому можно пробовать комбинировать 2 уравнения, как нам удобно.

Подсказка 2

Подсказка, если не догадались, как скомбинировать уравнения: нужно сложить первое*(3) и второе! И дальше уже магия выделений квадратов, у вас все получится!

Показать ответ и решение

Сложим первое уравнение, умноженное на $3$ , и второе. Получим,

2 2 40x +10y + 60x − 10y = −25

после деления на $10$ и преобразований, получаем: $4(x+ 3)2+(y− 1)2 = 0. 4 2$ Сумма двух квадратов может равняться нулю только в случае, когда каждый из этих квадратов равен нулю. Поэтому, ничего кроме $x= − 3,y = 1 4 2$ не может являться решением нашей системы.

Для окончания решения необходимо проверить, что найденные числа подходят:

{ 12⋅(− 3)2+4 ⋅(− 3)⋅ 1+ 3⋅(1)2+ 16⋅(− 3)= −6 4⋅(− 34)2− 12 ⋅(− 43)⋅2(1) +122⋅(− 3)− 104⋅ 1= −7 4 4 2 4 2

Ответ:

$x =− 3,y = 1 4 2$

Ошибка.
Попробуйте повторить позже

Задача 86#77814Максимум баллов за задание: 7

Найти все решения системы уравнений в действительных числах:

(| xy+ z+ t=1 |||{ yz+ t+x =3 | |||( zt+ x+ y = −1 tx+ y+z =1

Источники: Всесиб-2020, 11.1 (см. sesc.nsu.ru)

Подсказки к задаче

Подсказка 1:

Хмм... Сразу видно, что все уравнения в системе очень похожи друг на друга... На что намекают свободные коэффициенты и вид уравнений?

Подсказка 2:

Левые части соседних уравнений отличаются сдвигом переменных по циклу. При этом каждое уравнение содержит произведение и сумму двух переменных... Можно ли это как-то использовать?

Подсказка 3:

Конечно! Давайте вычтем уравнения друг из друга по циклу! Что можно сказать про их разности? К какому виду их левые части можно привести?

Подсказка 4:

Верно! Разность первого и второго уравнений выглядит так: xy-yz+z-x=-2. Заметим, что в левой части можно вынести (x-z). Получаем: (x-z)(y-1)=-2. Приведём к такому виду все полученные уравнения. Что можно заметить?

Подсказка 5:

Из второго уравнения следует, что (y-t) ≠ 0. Чему тогда равен x?

Подсказка 6:

Верно! x=1. Тогда из (x-z)(y-1) =-2 и (z-x)(t-1)=-2 следует, что y=2-t! Осталось только подставить выражения в изначальные уравнения и найти значения переменных!

Показать ответ и решение

(|xy+ z+t =1 (1) |||{yz+ t+x =3 (2) | |||(zt+x +y =−1 (3) tx+y +z =1 (4)

Сделаем следующие действия: $(1)− (2), (2)− (3), (3)− (4), (4)− (1).$ Разложим каждую разность на множители и получим:

(||(x− z)(y− 1)= −2 (5) ||{(y− t)(z− 1)= 4 (6) ||(z− x)(t− 1) =−2 (7) ||((y− t)(x− 1) =0 (8)

Из $(6)$ получаем $y− t⁄= 0,$ поэтому из $(8)$ имеем $x= 1.$ Из $(5)$ и $(7)$ получаем $x− z ⁄= 0 и y − 1 =1− t,$ откуда $y =2− t.$ Подставим найденные выражения в $(1)$ и $(2)$ и получим $z = −1,t= 2,$ откуда $y = 0.$ Таким образом, получаем единственное решение системы: $(1,0,−1,2).$

Ответ:

$(1,0,−1,2)$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 87#90858Максимум баллов за задание: 7

Найдите количество пар целых чисел $(x;y)$ , удовлетворяющих системе неравенств

{ y ≥ 90+ x− 690 y ≤ log x 6

Ответ должен быть представлен в виде алгебраической суммы не более трёх слагаемых.

Источники: Физтех - 2020, 11.7 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Давайте попробуем понять, при каких x вообще имеются решения. Для удобства давайте представим x в виде 6^t.

Подсказка 2

Используя неравенства системы, можно получить, что 90 + 6^t - 6^90 ≤ y ≤ t. Отсюда мы получаем, что 90 + 6^t - 6^90 - t ≤ 0. Что можно сказать про поведение выражения слева и как получить ограничения на t?

Подсказка 3

Давайте поймём, что для 1 ≤ x ≤ 6^90 решения есть? Кстати, сколько их при каждом каждом x? Что можно сказать про большие х?

Подсказка 4

Вопрос про количество решений при конкретном х был наводящим на конец решения. Исходя из системы неравенств это количество будет равно разности целой части логарифма и выражения 90 + x - 6⁹⁰. Осталось посчитать суммарное количество решений!

Показать ответ и решение

ОДЗ: $x> 0$

Заметим, что $t 90 90+ 6− 6 ≤y ≤t$ . Заметим, что если $t 90 f(t)= 90+ 6− 6 − t$ , то $′ t f (t)= 6ln6− 1$ и при $t> 1$ функция $f(t)$ возрастает. $f(90)= 0$ . Значит, $t≤ 90$ и $90 x ≤6$ . Заметим, что при $90 x ∈[6,6 ]$ функция $f(t)≥0,$ и значит, как минимум одно решение с таким $x$ есть. При $x ∈[1,6]$ такое решение тоже есть и это $y = 0$ .

Тогда нас интересует такая сумма

690 690 ∑ [log6x]− (90+x − 690)+1= (∑ [log6x]− x)+ (690− 89)690 x=1 x=1

Ее можно разложить на части

690 ( 89 6y+1−1 ) 89 ∑ [log6x]=( ∑ ∑ ([log6x])) +90= ∑ y(6y+1− 6y)+ 90= x=1 y=0x=6y y=0

89⋅690− 89⋅689+ 88⋅689− 88⋅688+ ...+ ⋅61− ⋅60+ 90=

690− 1 = 89⋅690 − 689− 688− ...− 1+90 =89⋅690−--5--+ 90

6∑90 90 90 x= 6-(6--+1) x=1 2

Итак,

6∑90 90 90 90 ( [log6x]− x)+(690 − 89)690 = 89⋅690− 6-− 1-+90− 6-(6-+-1) +(690− 89)690 = x=1 5 2

690− 1 690(690− 1) = −--5---+90+ ----2----

Ответ:

$− 690−1+ 90 + 690(690−1) 5 2$

Ошибка.
Попробуйте повторить позже

Задача 88#102367Максимум баллов за задание: 7

Решите систему уравнений

{ y2+ xy = 15; x2+ xy = 10.

Источники: ШВБ - 2020, 8 класс (см. olymp.bmstu.ru)

Подсказки к задаче

Подсказка 1

Хм, в обоих уравнениях слева есть общий множитель. Что можно с этим сделать?

Подсказка 2

Да, можно выразить/поделить одно уравнение на второе и аналогичные действия. Тогда получим соотношение между x и y, а значит, подставив его в одно из уравнений, получим квадратное и решим его, не забудем посчитать и вторую переменную!

Показать ответ и решение

{ y(y+ x) =15 x(x+ y) =10

Разделим первое уравнение системы на второе:

y 3 x = 2

3 y = 2x

Подставим в уравнение:

3 x2+ 2x⋅x= 10

[ x =− 2 x= 2

⌊ { | y = −3 ||| { x= −2 ⌈ y = 3 x = 2

Ответ:

$(−2;−3),(2;3)$

Ошибка.
Попробуйте повторить позже

Задача 89#102527Максимум баллов за задание: 7

Восемь чисел $a,a ,a ,a 1 2 3 4$ и $b,b,b,b 1 2 3 4$ удовлетворяют соотношениям

(| a b + ab = 1 |||{ 1 1 2 3 | a1b2+ a2b4 = 0 |||( a3b1+ a4b3 = 0 a3b2+ a4b4 = 1

Известно, что $a2b3 = 7$ . Найдите $a4b4$ .

Источники: Межвед - 2020 (см. v-olymp.ru)

Подсказки к задаче

Подсказка 1

a₄b₄мы сможем выразить через a₂b₃. Но что делать дальше?...через какое произведение хочется выразить a₂b₃?

Подсказка 2

Попробуйте доказать, что a₂b₃ = a₃b₂.

Подсказка 3

Давайте скомбинируем уравнения с помощью коэффициентов, чтобы выразить b₂ и b₃ через a₂ и a₃ ;)

Показать ответ и решение

Докажем, что $ab = a b 23 32$ . Умножим уравнение (a) исходной системы

(| ab + ab = 1 а |||{ 1 1 23 | a1b2+ a2b4 = 0 б |||( a3b1+ a4b3 = 0 в a3b2+ a4b4 = 1 г

на $b2$ и вычтем из него уравнение (б), умноженное на $b1$ . В результате получим

a2⋅Δ = b2.

Здесь $Δ = b2b3− b1b4$ . Аналогично, из (в) и (г) находим, что

a ⋅Δ = b. 3 3

Заметим, что $Δ ⁄=0$ , так как в противном случае из (3) следовало бы, что $b3 = 0$ , а значит и $a2b3 =0$ , что противоречит условию задачи. Остается выразить $a2$ и $a3$ из (2) и (3) и подставить полученные выражения в (1). Справедливость соотношения (1) будет тем самым доказана. Далее из уравнения (г) и равенства (1), следует, что $a4b4 =$ $1 − a3b2 = 1− a2b3 = −6$ .

_________________________________________________________________________________________________________________________________________________________________________________

Замечание.

Система уравнений в задаче — это покомпонентная запись матричного равенства:

( 1 0 ) ( a1 a2 ) ( b1 b2 ) A ⋅B = 0 1 , где A = a3 a4 и B= b3 b4 .

Хорошо известно, что если произведение двух матриц равно единичной, то такие матрицы коммутируют, а значит система уравнений в задаче останется справедливой, если в ней все $ai$ заменить на $bi$ и наоборот. Из этого наблюдения равенство (1) следует немедленно.

Ответ: -6

Ошибка.
Попробуйте повторить позже

Задача 90#78976Максимум баллов за задание: 7

Положительные числа $a,b$ и $c$ таковы, что выполнены равенства

2 2 2 2 2 2 a +ab+ b =1, b+ bc+c = 3, c + ca +a = 4.

Найдите $a +b+ c$ .

Подсказки к задаче

Подсказка 1

Давайте немного остановим свой взгляд на равенства из условия. Можно сказать, что нам дали идентичные выражения. Где ещё с таким видом равенств вы могли встречаться?

Подсказка 2

Точно, это же теорема косинусов для угла в 120 градусов. Так давайте же попробуем это изобразить на рисунке. Какая фигура там получается?

Подсказка 3

Верно, получается прямоугольный треугольник, а внутри него точка, из которой все стороны видны под углом 120 градусов. Причём расстояние от точки до вершин треугольника и есть наши a, b, c. А у нас просят найти их сумму. Хм, чтобы тогда хорошо сделать... Что будет с нашими отрезками, если повернуть наш треугольник на 60 градусов вокруг вершины с углом 90 градусов?

Подсказка 4

Верно, если посчитать углы и воспользоваться простым свойствами поворота, то получится, что наши отрезки "выпрямляются". То есть мы получили треугольник с известным углом и смежными сторонами, а напротив как раз то, что надо найти. Осталось только воспользоваться известной теоремой, и победа!

Показать ответ и решение

Первое решение.

Отложим из одной точки $T$ отрезки $TA, T B и TC$ с длинами $a, b и c$ соответственно так, чтобы $∘ ∠AT B = ∠BT C = ∠CT A= 120.$

Тогда по теореме косинусов при учете соотношения $∘ 1 cos120 = −2,$ получаем, что $√ - AB = 1,BC = 3,CA = 2.$ Видим, что по теореме Пифагора треугольник $ABC$ прямоугольный $∘ (∠B = 90 ),$ причем его катет $AB$ в два раза короче гипотенузы $AC,$ откуда следует равенства $∘ ∘ ∠BAC = 60 ,∠BCA =30 .$

Отметим точку $B1$ — середину гипотенузы $AC$ и точку $C1,$ что $△ABC = △AB1C1$ и точки $C1$ и $B$ по разные стороны от $AC :$

$PIC$

По построению треугольники $ABC$ и $AB1C1$ отличаются поворотом на $60∘$ с центром в точке $A.$ Отметим точку $T1$ в треугольнике $AB1C1,$ соответсвующую точке $T$ в треугольнике $ABC.$ Тогда $BT = B1T1, CT = C1T1, и AT = AT1 = TT1.$ Последнее равенство обусловлено тем, что треугольник $AT T1$ получается равносторонним, поскольку точки $T$ и $T1$ отличаются поворотом на $60∘$ с центром в точке $A.$

Осталось отметить, что точки $B, T, T1, C1$ лежат на одной прямой, поскольку $∠ATB = ∠AT1C1 = 120∘ и ∠ATT1 =∠AT1T = 60∘.$ В итоге получаем, что

a+ b+ c= AT + BT +CT = BT +T T1 +T1C1 = BC1,

а $BC1$ может быть вычислено из теоремы косинусов для треугольника $BAC1 :$

BC2 = AB2 +AC2 +AB ⋅AC = 1+ 4+1 ⋅2 =7. 1 1

Второе решение.

Вычтем из первого равенства второе. Получим $(a− c)(a+c)+ b(a− c)=− 2,$ т.е.

-−2- a +b+ c= a− c

Аналогично, вычитая из второго равенства третье и из третьего первое, получим

−2 −1 3 a+ b+ c= a−-c = b−-a = c−-b

Если обозначить $s=a +b+ c,$ то можно переписать предыдущее соотношения как

a− c=− 2s−1, b− a= −s−1, c− b= 3s−1

Теперь сложим все исходные равенства:

2a2+ 2b2+ 2c2 +ab+ bc +ca= 8

(1)

Нетрудно заметить, что левую часть можно выразить следующим образом:

2 1 2 2 2 (a+ b+c) + 2((a− c)+ (b− a) + (c− b))= 8

что означает

2 1 −2 −2 −2 s + 2(4s + s + 9s )= 8

Домножением на $s2$ получаем биквадратное уравнение

s4 − 8s2+ 7=0

корнями которого являются $2 2 s = 1 и s =7.$ Однако первое из значений явно вступает в противоречие с равенством $(1):$

2 2 2 2 2 1 1 1 s = (a+b +c) >a + b + c+ 2ab+ 2bc+ 2ca =4.

Значит, остается $s2 = 7,$ т.е. $√ - a+ b+c = 7.$

Ответ:

$√7$

Ошибка.
Попробуйте повторить позже

Задача 91#102368Максимум баллов за задание: 7

Решите систему уравнений

{ 3x − y− 3xy = −1; 9x2y2+ 9x2+ y2− 6xy =13.

Подсказки к задаче

Подсказка 1

В этой задаче стоит поработать с более простым уравнением — первым. Попробуйте его преобразовать!

Подсказка 2

Кажется, вы уже смогли разложить первое уравнение на скобки. Если нет, то обязательно разложите. Кажется, теперь задача свелась к подстановке известного значения во второе равенство и решение квадратного уравнения)

Показать ответ и решение

{ (1− y)(3x+1)= 0 9x2y2+ 9x2+y2− 6xy = 13

⌊ { 1− y = 0 || 9x2y2+9x2+ y2− 6xy = 13 ||⌈ { 3x+1 =0 9x2y2+9x2+ y2− 6xy = 13

Решим каждую систему совокупности:

{ { y =1 x =− 13 9x2 +9x2+ 1− 6x =13 или 9(− 13)2y2+ 9(− 13)2+ y2+ 6y13 = 13

( ( |{ [ y = 1 |{ [x =− 13 | x= − 23 или | y =3 ( x = 1 ( y =2

Ответ:

$(− 2;1),(1;1),(− 1;−3),(− 1;2) 3 3 3$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 92#32378Максимум баллов за задание: 7

Числа $x$ и $y$ таковы, что выполняются равенства

siny +cosx= sin3x и sin2y− sin2x= cos4x − cos2x.

Какое наименьшее значение может принимать сумма $cosy+ sinx$ ?

Подсказки к задаче

Подсказка 1

Очевидно, что задача на некие тождественные преобразования, то есть что-то выразить, куда-то подставить и получить ответ. Посмотрим на оба уравнения. Что из этого наиболее приятно для преобразований? Первое? Вряд ли, cos(x) и sin(3x) почти никак не связаны, что то общее вынести вряд ли получится. А вот второе… Да, там ,сущностно, косинусы двойного угла и обычного (2х и 4х) и синус обычного. С этим можно поработать. К примеру расписать разность косинусов.

Подсказка 2

Расписав разность косинусов, мы получим 2sin(x)3x. Но ведь в синусе двойного угла тоже есть 2sin(x). То есть можно вынести. А что останется в скобках после вынесения? Где это еще есть?

Подсказка 3

В скобках останется cos(x)-sin(3x). Но ведь мы можем подставить значение этого из первого уравнения. А еще, ведь это все мы преобразовывали равенство sin(2y)=sin(2x)+cos(4x)-cos(2x)=-2sinx*sin(y). При этом sin(y) есть и слева и справа. Значит, преобразовывая это выражение, мы получили, что либо sin(y)=0 , либо sin(x)+cos(y)=0. Второй случай сразу дает один из ответов. А что делать в первом?

Подсказка 4

Конечно, подставлять, что же тут еще делать) А куда? В первое, поскольку тогда получим уравнение на x. Выходит, что cos(x)=sin(3x). Значит, cos(x)=cos(pi/2-3x). Значит +-x=pi/2-3x+2pi*k, y=pi*n. Осталось найти значения cos(y) и sin(x) для найденных выше решений и выбрать наименьший из всех.

Показать ответ и решение

Из второго равенства

sin2y = sin2x+ (cos4x− cos2x)= 2sinxcosx− 2sin3xsinx= 2sin x(cosx− sin 3x)

Подставим $cosx− sin3x$ в первое равенство из условия

2sin ycosy =sin2y =− 2sinxsiny ⇐⇒

[ siny =0 sinx +cosy = 0

Во втором случае искомое по условию выражение равно нулю. Посмотрим, будет ли оно меньше в первом случае.

В первом случае $y =πn,n ∈ℤ$ , и тогда из первого равенства

( ) cosx− sin3x= 0⇐⇒ cosx− cos π− 3x = 0⇐⇒ 2sin(π − x)sin(π − 2x)= 0 2 4 4

То есть $x= π+ πk,k∈ℤ 4$ или $x = π+ πk,k∈ℤ. 8 2$

Минимум суммы получаем при $cosy = −1 ⇐⇒ y = π+ 2πn,n∈ ℤ$ и $x= − 3π+ 2πk,k ∈ℤ. 8$

Посчитаем синус:

( ) ∘ --√-- cos 2⋅ 3π =cos3π =− 1√--=1 − 2sin2 3π =⇒ sin 3π-=-2+--2 8 4 2 8 8 2

Тогда искомое по условию выражение равно

∘2+-√2 cosy+ sinx =−1 − --2----

Получили значение меньше, чем во втором случае (меньше нуля), поэтому оно является ответом.

Ответ:

$− 2+√2+√2 2$

Ошибка.
Попробуйте повторить позже

Задача 93#49483Максимум баллов за задание: 7

Решите систему уравнений

(| x2 = (y− z)2− 3; { y2 = (z− x)2− 7; |( 2 2 z = (x− y) + 21.

Источники: ОММО-2018, номер 5, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

хм, пока не очень понятно, что можно сделать с этими уравнениями, а давайте попробуем перенести квадрат разности в другую часть и естственно применить разность квадратов.

Подсказка 2

заметим, что множители в наших трех итоговых уравнениях частично совпадают! // для удобства можно заменить их на a, b, c. тогда у вас есть ab, bc и ac, а надо найти каждое по отдельности, для этого помогло бы узнать abc, например!

Показать ответ и решение

Перенесём в каждом уравнении квадрат разности в левую части и применим формулу для разности квадратов:

(| (x− y +z)(x +y− z)= −3 { (y− z +x)(y +z− x)= −7 . |( (z− x +y)(z +x− y)= 21

Обозначим $X = −x+ y+ z,Y = x− y+ z,Z =x +y − z$ . Тогда

(| YZ =− 3 { ZX =− 7 |( XY = 21

Перемножая все получившиеся равенства, имеем $(XY Z)2 = 3⋅7⋅21$ , откуда $XY Z =21$ или $XYZ = −21.$

Разберём случай $XYZ = 21$ . В нём $X = (XYZ)∕(YZ)= −7,Y = −3,Z =1$ ; тогда $x= Y+2Z-=$ $− 1,y =− 3,z = −5.$

Второй случай разбирается аналогично и в нём $x= 1,y = 3,z = 5.$

Ответ:

$(−1,−3,− 5),(1,3,5)$

Ошибка.
Попробуйте повторить позже

Задача 94#91381Максимум баллов за задание: 7

Решить в действительных числах систему уравнений:

{ x2+ xy+y2 = 4, 4 22 4 x + xy + y = 8.

Показать ответ и решение

Рассмотрим случаи.

1) $x= y$ , тогда $2 4 3x = 4, 3x = 8$ , откуда $2 x = 2$ , что явно не удовлетворяет обоим уравнениям. Решений нет.

2) $x= −y$ , тогда $2 4 x =4, 3x = 8$ , откуда $2 2 x = 3$ что тоже явно не удовлетворяет обоим уравнениям. Решений нет.

3) $x⁄= ±y$ . Домножим первое уравнение на $x − y$ . получим $3 3 x − y =4(x− y)$ . Домножим второе уравнение на $2 2 x − y$ , получим

( ) x6− y6 =8 x2− y2

Поделим второе уравнение на первое, получим

3 3 x +y = 2(x+y),

откуда

2 2 x − xy+ y =2.

С учётом первого уравнения, $xy = 1,x2y2 = 3.$ Заменяя $y = 1 x$ , получаем биквадратное уравнение $x4− 3x2 +1= 0$ , откуда $∘3±√5- ∘ 3∓√5- x =± 2 ,y = ± 2$ – всего 4 решения.

Ответ:

$(∘-3+√5,∘ 3−√5) 2 2$ , $( −∘-3+√5,−∘ 3−√5) 2 2$ , $(∘ 3−-√5,∘ 3+√5) 2 2$ , $(−∘ 3−√5,− ∘-3+√5) 2 2$

Ошибка.
Попробуйте повторить позже

Задача 95#31173Максимум баллов за задание: 7

Решите в действительных числах систему уравнений

(| x+ y+ 2− 4xy = 0; { y+ z+2 − 4yz = 0; |( z+ x+ 2− 4zx= 0.

Источники: ОММО-2017, номер 5, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Везде одинаковая структура прям, всё симметрично, в этот момент должно появиться желание вычесть одно из другого. Что именно? Да всё подряд!

Подсказка 2

Да, после попарного вычитания (т. е. из (1) вычли (2), из (2) - (3) и тд) получаем произведения, равные нулю. Может ли, например, 1-4z равняться нулю? Почему?

Показать ответ и решение

Попарно вычтем уравнения друг из друга, получим:

(| x+ y− 4xy− y− z+ 4yz =0 (| (x − z)(1− 4y)= 0 { y+ z− 4yz− z− x+ 4zx =0 ⇐⇒ { (y − x)(1 − 4z)= 0 |( |( z+ x− 4zx− x− y+ 4xy =0 (z − y)(1− 4x)= 0

Пусть любая из переменных равна $1∕4$ — выберем $x$ в силу симметрии, тогда из первого уравнения системы $1∕4+ y+ 2− y = 0$ - неверно, то есть все переменные не равны $1∕4$ , откуда сразу же $x =y =z$ , снова подставим в первое уравнение системы (пользуемся симметрией) и получим $2x2− x− 1= 0=⇒ x= 1±3 =− 1,1 4 2$ , откуда и получим ответ.

Ответ:

$(−1∕2,− 1∕2,−1∕2),(1,1,1)$

Ошибка.
Попробуйте повторить позже

Задача 96#49484Максимум баллов за задание: 7

Решите систему уравнений

(| √x = y+z; { √y = z+2x-; |( √- x+2y- z = 2 .

Подсказки к задаче

Подсказка 1!

1. давайте попробуем поиграться с оценками в этой задаче, так как уравнения как бы зациклены. давайте упорядочим числа, например х <= y <= z и попробуем тогда оценить корни x и z через соответсвующие переменные. то есть корень из х нам нужно оценить через х, используя уравнение из условия и наше упорядочивание. то есть два слагаемых из правой части оцениваем в соответсвии со знаками между x, y, z и получаем, что корень из х, например, больше х. тогда можно сделать вывод о том, какому промежутку х принадлежит - [0, 1] или [1, ∞].

Подсказка 2!

2. теперь попробуем это использовать - заметим, что z принадлежит [1, ∞], а х [0, 1]. тогда из первого уравнения (y+z)/2 это тоже число из [0, 1]. и аналогично рассмотрим третье уравнение, для него аналогично проводим оценку, но с числом из [1, ∞].

Подсказка 3!

3. осталось аккуратно вывести к тому, что и чисел должны быть определенные значения, чтобы все оценки сошлись!

Показать ответ и решение

Первое решение.

На ОДЗ все переменные неотрицательны. Если хотя бы одна равна нулю, то сумма остальных также нулевая и все переменные равны $0$ . Учтём это и далее будем считать, что все переменные больше нуля.

Не умаляя общности (в силу симметрии), пусть $x≤ y ≤ z$ , тогда посмотрим на первое уравнение

√- y+z x+ x x = -2--≥ -2--= x ⇐⇒ x∈ [0,1]

При этом для последнего уравнения

√ - z = x+2-y≤ z+2-z= z ⇐⇒ z ≥ 1

Итак, с одной стороны $- √x ∈[0,1]$ и $y+z2-∈[0,1] ⇐⇒ y+ z ∈[0,2] =⇒ y ∈[0,1]$ (поскольку $z ≥ 1$ ). С другой стороны, $- √z ≥ 1$ , откуда $x+2y≥ 1 =⇒ x= y = 1$ (поскольку только в этом случае возможно равенство). Отсюда сразу же получаем $z =1.$

Второе решение.

ОДЗ: $x≥ 0,y ≥0,z ≥ 0$ . Пусть, не умаляя общности, $x ≤y ≤z.$

К неотрицательным числам мы имеем право применить неравенство о средних для двух чисел:

(|{ √x= y+2z≥ √yz; √y = z+2x≥ √zx; |( √z = x+2y≥ √xy.

Перемножая неотрицательные части всех неравенств системы получаем следствие $√xyz ≥ xyz.$ Отсюда

xyz ≤ 1 (*)

Докажем, что для нетривиального ( $0,0,0)$ решения системы в этом неравенстве должно достигаться равенство.

Сложим три уравнения исходной системы:

√x+ √y +√z-= x+y +z

Нам подходит случай $x =y =z =0,$ эта тройка удовлетворяет исходной системе. Иначе из равенства выше делаем вывод, что все три числа меньше единицы быть не могут, ведь тогда левая часть равенства очевидно окажется больше правой (для $t= 0 √t =t,$ для $0 <t< 1 √t->t).$

Рассмотрим тогда случай, когда ровно два числа меньше единицы: $x ≤y <1 ≤z$ . Но тогда и третьей число оказывается меньше единицы: $√z = x+y< 1+1 =⇒ z < 1. 2 2$

Рассмотрим случай, когда ровно одно число меньше единицы: $x< 1≤ y ≤ z.$ Но это противоречие $1> √x= y+z≥ 1+1= 1. 2 2$

Остаётся случай, когда $1 ≤x ≤y ≤z.$ Но тогда $1 ≤xyz.$ Но из (*) $xyz ≤ 1$ (это было следствие системы после применения неравенства о средних). Остаётся только вариант, чтобы в неравенстве достигалось равенство, для (*) это, как известно, происходит при равенстве чисел. Из системы получаем $x= y = z = 1.$

Ответ:

$(0;0;0),(1;1;1)$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 97#36910Максимум баллов за задание: 7

Решите систему уравнений:

{ x2− xy+ y2 =19; x4+ x2y2 +y4 = 931.

Источники: ОММО-2016, номер 5, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Вы тоже это заметили? Сначала написали x²+y², а потом стало x⁴+y⁴, сначала было ху, стало (ху)² -> делаем замену!

Подсказка 2

Да, двойная замена: сумма квадратов - это а, произведение - b. Чтобы получить второе уравнение, достаточно записать a²-b². Когда станет известно, чему равны а и b, сделаем обратную замену.

Показать ответ и решение

Функция $f(x,y)$ двух переменных $x$ и $y$ называется симметрической, если $f(y,x)= f(x,y)$ . В симметрической системе можно сделать замену $2 2 2 u= (x+y) = x + y +2xy,v = xy$ , тогда система эквивалентна:

{ u− 3v =19 2 2 (u − 2v) − v = 931

{ u= 3v+19 (v+ 19)2 − v2 = 931

{ u= 3⋅15+ 19 v = 15

Обратная замена:

{ (x+ y)2 = 64 xy = 15

По обратной теореме Виета решения системы удовлетворяют одному из уравнений: $t2± 8t+15= 0$ , решая которые получаем ответ.

Ответ:

$(3,5),(−3,−5),(5,3),(− 5,−3)$

Ошибка.
Попробуйте повторить позже

Задача 98#79923Максимум баллов за задание: 7

Найдите все пары положительных чисел $(x,y)$ , удовлетворяющих системе уравнений

({ √-- ∘ y- y − 2 xy − x + 2= 0 ( 3x2y2+ y4 =84

Подсказки к задаче

Подсказка 1

Какие-то неприятные выражения с x и y... Сделайте замену!

Подсказка 2

Пусть v = √(xy), u = √(y/x).

Показать ответ и решение

Обозначим $∘ y= u, √xy-= v x$ (при этом $u> 0, v > 0$ ). Тогда $uv = ∘-y⋅√xy = ∘y2-=|y|=y x$ , $v = √xy :∘ y= √x2-=|x|=x u x$ , так как по условию $x$ и $y$ положительны. Система принимает вид

{ uv− 2v− u+ 2= 0, { (v− 1)(u− 2)= 0 4 44 ⇔ 4 4 4 3v + u v =84 3v + u v = 84

Из первого уравнения следует, что $v = 1$ или $u= 2$ . Если $v = 1$ , то $3+u4 =84$ , откуда $u= 3$ ; тогда $x= v = 1,y =uv =3 u 3$ . Если $u =2$ , то $4 4 3v + 16v =84$ , откуда $4∘-84- v = 19$ ; тогда $v 4∘21 4∘ 84- x= u = 76,y = uv = 2⋅ 19$ .

Ответ:

$(1;3),(4∘-21;2⋅ 4∘ 84) 3 76 19$

Ошибка.
Попробуйте повторить позже

Задача 99#93103Максимум баллов за задание: 7

Решите систему уравнений

{ x+ √x+-2y− 2y = 7 x2+x +2y− 4y2 =227 2

Подсказки к задаче

Подсказка 1

Попробуйте преобразовать нижнее уравнение.

Подсказка 2

Воспользуйтесь формулой разности квадратов. Можно ли сделать замену?

Подсказка 3

Пусть a = x - 2y, b = √(x + 2y).

Показать ответ и решение

Пусть $x − 2y = a,√x+-2y = b≥0$ . Тогда

(| 7 |{ a+ b= 2 (1) ||( 2 2 27 b a+ b= 2 (2)

Из $(1)$ получаем, что $7 a= 2 − b.$ Подставим во $(2):$

2( 7 ) 2 27 b 2 − b + b = 2

Домножим обе части уравнения на $2$ и раскроем скобки:

−2b3+ 7b2+2b2 = 27

2b3 − 9b2− 27 =0

Подберём корни: $b= 3$ — один из корней. Тогда вынесем $(b− 3)$ за скобки:

2 (b− 3)(2b − 3b− 9)=0

Найдём корни второй скобки: $b1 = 3,b2 = − 3 2$ — не подходит, так как $b≥ 0.$ Значит, единственное возможное значение $b$ — это $3.$

Тогда $a = 7− b= 1. 2 2$ Получаем систему:

(| 1 { x − 2y = 2 (3) |( x +2y = 9 (4)

Отсюда получаем, что $x= (3)+(4)= 19,y = (4)−-(3)= 17. 2 4 4 8$

Таким образом, система уравнений имеет единственное решение — $(19 17) 4 ;8 .$

Ответ:

$(19;17) 4 8$

Ошибка.
Попробуйте повторить позже

Задача 100#31181Максимум баллов за задание: 7

Решите систему

(| 1 + 1--= − 2-; |{ x1 y+1z- 125 ||( y1 +-x+1z = −31; z +x+y = −4.

Источники: Физтех-2015, 11.3 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Домножим на знаменатели, учитывая все ограничения, и сложим три уравнения, упростив итоговое.

Подсказка 2

Мы смогли выразить три попарных произведения через x+y+z и какой-то коэффициент. Учитывая ограничения, мы на сумму переменных запросто можем поделить, а значит выразить две каких-то буковки через третью и найти её :)

Показать ответ и решение

Домножив каждое уравнение на произведение знаменателей, получим систему

( −7,5(x+ y+ z)= xy+ xz |{ |( −1,5(x+ y+ z)= xy+ yz −4(x +y+ z)= xz+yz

Сложив почленно все три уравнения и разделив полученное равенство пополам, получаем равенство

xy+ xz+ yz =− 6,5(x+ y+z)

Вычитая из него каждое из уравнений последней системы, находим, что

(|{ − 2,5(x+ y+z)= xy (x+ y+ z)=yz |( − 5(x+ y+ z)=xz

Разделив первое уравнение на второе (это возможно, так как из ОДЗ исходной системы следует, что $xyz ⁄=0$ ), получаем, что $x =− 2,5z$ , а разделив первое на третье - что $y = 0,5z$ . Тогда второе уравнение принимает вид $− z = 0,5z2$ , откуда $z =−2,x= 5,y = −1$ .

Ответ:

$(5;− 1;−2)$

Следующая подтема