Тема АЛГЕБРА

Системы уравнений и неравенств

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела алгебра

Разделы подтемы Системы уравнений и неравенств

Арифметические операции над системой

Замены переменных

Оценки в системах

Симметрия или цикличность в системе

Однородные и сводящиеся к ним

Сведение системы к квадратному

Системы неравенств

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 101#49482Максимум баллов за задание: 7

Решите систему уравнений

{ 26x2 +42xy+ 17y2 = 10; 10x2 +18xy+ 8y2 =6.

Источники: ОММО-2015, номер 5, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

О, две формулы, похожие на квадраты суммы! Только коэффициенты какие-то лютые...

Подсказка 2

Если 26 и 10 или 17 и 8 вычесть, то получится квадрат. Да и если сложить, вообще-то тоже! Так давайте сложим и вычтем уравнения системы

Подсказка 3

Не забываем, что когда квадрат равен какому-то положительному числу, возникает два случая!

Показать ответ и решение

Складывая и вычитая два уравнения системы, получаем, что исходная система эквивалентна следующей:

({(6x+ 5y)2 = 16 2 ((4x+ 3y) = 4

Откуда получаем 4 возможных случая

{ { { { 6x +5y = 4 6x+ 5y =4 6x +5y = −4 6x+ 5y = −4 4x +3y = 2 4x+ 3y =− 2 4x +3y = 2 4x+ 3y = −2

Решая каждую из этих систем, находим 4 ответа: $(−1,2),(− 11,14),(11,−14),(1,− 2)$ .

Ответ:

$(−1,2),(− 11,14),(11,−14),(1,− 2)$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 102#70347Максимум баллов за задание: 7

Числа $x$ и $y$ удовлетворяют условиям $x2+ y2 = 1$ и $20x3− 15x =3.$ Найдите $|20y3− 15y|.$

Источники: СпбОШ - 2015, задача 11.3(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1

Не напоминает ли нам первое условие какую-нибудь теорему из области тригонометрии? Возможно, это даст нам неплохую идею для замены!

Подсказка 2

Итак, первое уравнение позволяет нам заменить одну из переменных на синус, а вторую — на косинус. Но что же делать дальше? Какую формулу напоминает второе условие, после вынесение общего множителя слева за скобки?

Подсказка 3

Удивительно! Второе условие и неизвестное выражение очень напоминают нам тригонометрические формулы для тройных углов, с точностью до умножения на коэффициент. Осталось лишь чуть-чуть повычислять, снова вспомнить об ОТТ и задача решена!

Показать ответ и решение

Первое решение.

Подберём $α$ таким образом, чтобы выполнялось равенства $x= sin(α),y = cos(α).$ Тогда $3 3 sin(3α)= 3sin(α)− 4sin (α)=3x− 4x = −3∕5.$ Следовательно,

3 3 |20y − 15y|= |20cos(α)− 15cos(α)|=

∘-----2--- = |5cos(3α)|= 5 1 − sin (3α) =4

Второе решение.

Найдём значение выражения $|4y3− 3y|.$ Для этого достаточно найти значение его квадрата, а потом извлечь корень. Но квадрат этого выражения равен

3 2 2 2 2 4 2 |4y − 3y|= y (4y− 3) =y (16y − 24y + 9).

Подставим $1− x2$ вместо $y2,$ преобразуем и получим выражение

6 4 2 2 2 (3)2 16 − 16x + 24x − 9x + 1= 1− x(4x− 3) = 1− 5 = 25-

Следовательно, $()2 |4y3− 3y|2 = 45 ,$ откуда и находим ответ.

Ответ:

$4$

Ошибка.
Попробуйте повторить позже

Задача 103#31983Максимум баллов за задание: 7

Решите систему уравнений

{ x2− 4xy+ 4y2 = 2x− 4y+3; √3x-− 6y = 2− xy.

Источники: Физтех-2014, 11.3 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Вспомните формулы сокращённого умножения.

Подсказка 2

Сделайте замену t = x - 2y.

Показать ответ и решение

С учётом замены $t=x − 2y$ первое уравнение равносильно $t2 = 2t+3 ⇐⇒ t= −1$ или $t=3$ , однако для неотрицательности подкоренного во втором уравнении $t≥ 0$ , откуда подходит только $t= x− 2y = 3$ . С учётом первого уравнения системы второе уравнение превращается в $2− xy = 3⇐ ⇒ xy = −1$ . Мы преобразовали систему из условия к:

{ x= 2y+3; (2y+ 3)y +1= 0.

Тогда $y = −3±√9−-8,x = −3±1-+3 = 3±1- 4 2 2$ .

Ответ:

$(1;− 1),(2;−1∕2)$

Ошибка.
Попробуйте повторить позже

Задача 104#77811Максимум баллов за задание: 7

Решите систему

(| -xy-= 1; |{ x+yzy ||( y+xzz = 2; x+z = 3.

Подсказки к задаче

Подсказка 1

Давайте подумаем, что мы можем здесь сделать. Если не брать правые части уравнений, то выражения симметричны относительно переменных, которые в нем содержатся(хотя это вовсе не значит, что система симметрична). Это значит, что мы можем каким-то образом привести наши уравнения к нужному виду так, чтобы наши выражения относительно каждой из переменных были симметричны(то есть, на данный момент у нас в левой части каждого уравнения находится некоторое выражение, которое зависит и от x и от y(к примеру), а мы хотим, чтобы слева была сумма двух структурно одинаковых выражений, каждое из которых зависит только от одной переменной, ведь тогда мы сможем, сделав замену, просто-напросто решить линейную систему и все). Как это можно сделать?

Подсказка 2

Попробуйте перевернуть каждую из дробей слева и написать систему в виде (x + z)/xz = 1/3. Как тогда можно по-другому написать каждое из наших выражений слева, чтобы получилась сумма, структурно одинаковых выражений?

Подсказка 3

Верно, нужно расписать каждую дробь, как сумму обратных к переменным. Тогда, у нас получится система линейных уравнений на три переменных, которую мы умеем решать.

Показать ответ и решение

"Перевернём" каждое из уравнений системы:

(| x+y =1 |{ yx+yz 1 ||( xyz+z= 21 xz = 3

Преобразование равносильно, т.к. ни одна из правых частей не может обратиться в ноль.

Заметим, что $x+y = 1 + 1 xy x y$ и т.д.

Поэтому мы получили систему линейных уравнений на $1 1 x,y$ и $1 z.$

Решая её, получаем $1 -5 1 -7 1 1- x =12,y = 12,z = − 12.$

Ответ:

$(12;12;− 12) 5 7$

Ошибка.
Попробуйте повторить позже

Задача 105#64396Максимум баллов за задание: 7

Решите систему неравенств

{ 2x2+ 4xy +11y2 ≤ 1; 4x+ 7y ≥ 3.

Источники: ДВИ - 2011, вариант 1, задача 8 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Выделите полный квадрат в первом уравнении системы. Не напрашивается ли сюда какая-нибудь замена?) Пусть, например, u = x + y, а v = 3y

Подсказка 2

Перепишите систему после замены. Попробуйте теперь сложить два неравенства, предварительно умножив одно из них на коэффициент так, чтобы в итоге в правой части сумма была ноль!

Подсказка 3

Давайте повыделяем полные квадраты. И, кажется, у нас вышла красота: сумма двух квадратов меньше, либо равна нулю... Сделайте выводы!

Показать ответ и решение

Перепишем систему

{ 2x2+ 4xy+ 11y2 ≤ 1 { 2(x+ y)2+ (3y)2 ≤ 1 4x +7y ≥ 3. ⇐⇒ − 4(x+ y)− 3y ≤ −3

Пусть $x+y =u,3y = v$ . Получим систему

{ 2u2+ v2 ≤ 1 { 6u2+3v2− 3≤ 0 − 4u − v ≤− 3 ⇐⇒ −8u− 2v+ 6≤0

После сложения получаем

6u2− 8u+ 3v2 − 2v+ 3≤ 0

( ) ( ) 6 u2− 2 ⋅u ⋅ 2+ 4 + 3 v2− 2⋅v⋅ 1 + 1 ≤ 0 3 9 3 9

( )2 ( )2 6 u− 2 + 3 v − 1 ≤0 3 3

2 1 u= 3,v = 3

Легко проверить, что эта пара подходит и в систему неравенств до сложения, потому что неравенства обращаются в равенства. После обратной замены получаем

{ 2 x +y1= 3 y = 9

Откуда $x= 5. 9$

Ответ:

$(5,1) 9 9$

Ошибка.
Попробуйте повторить позже

Задача 106#90592Максимум баллов за задание: 7

Решите систему

(| x+ y+z =13 { x2+y2+ z2 = 61 |( xy+xz =2yz.

Подсказки к задаче

Подсказка 1

Хм, кажется из всех данных уравнений кажется легко составить квадрат суммы (x + y + z). А что же делать теперь? Если очень внимательно посмотреть на то, что мы получили, можно без труда выразить произведение yz.

Подсказка 2

Теперь мы можем выразить x сразу из двух уравнений....Кажется осталось соединить полученные знания и досчитать значения оставшихся неизвестных.

Показать ответ и решение

Распишем $(x+ y+ z)2$ двумя разными способами. С одной стороны из первого уравнения системы получаем, что

2 (x+y +z) = 169

С другой стороны,

2 2 2 2 (x+ y+z) = x +y + z + 2(xy+ xz+ yz)

Подставляя второе и третье уравнение из системы, получаем, что

(x+ y+z)2 = 61+2(2yz+yz)= 61+6yz

Тогда

61+ 6yz =169 =⇒ yz =18

Выразим $y+ z$ из первого уравнения и подставим в третье:

{ [ y+ z = 13 − x =⇒ x2− 13x+ 36= 0 =⇒ x =4 x(13− x)= 2yz =36 x =9

(a) $x= 4:$

{ { y+z =9 =⇒ z = 9− y =⇒ y2− 9y+ 18= 0 y2 +z2 = 45 y2+(9− y)2 =45

Тогда получаем

[ y = 3 =⇒ z = 6 y = 6 =⇒ z = 3

(b) $x= 9:$

{ y+ z = 4 { z = 4− y y2+ z2 =45 =⇒ y2+ (4 − y)2 = −20 =⇒ y2− 4y+ 18 =0

Тогда получаем, что нет решений, так как у последнего уравнения $D < 0.$

Ответ:

$(4;3;6), (4;6;3)$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 107#49486Максимум баллов за задание: 7

Решите систему уравнений

(| 2x2 = yz− 2x; { 2y2 = −xz+ 2y; |( 2 2z = −xy+ 2z.

Подсказки к задаче

Подсказка 1!

1. заметим, что у нас уравнения симметричные. тогда вычтем, например, из второго третье и разложить на множители. из-за симметрии и слева, и справа будет общий множитель (y-z). тогда можно на него сократить и выразить из оставшегося х через y и z! // не забываем, что нельзя делить на ноль

Подсказка 2!

2. осталось аккуратно подставить, разобрать оба случая (деление на ноль и нет деления на ноль), не забываем сделать проверку, если у вас неравносильные переходы

Показать ответ и решение

Вычтем третье уравнение из второго

2 2 2(y − z)= x(y− z)+ 2(y − z) ⇐⇒ z− y = 0 или 2y+ 2z = x+2

В первом случае подставим $z = y$

{ 2x2 = z2 − 2x 2z2 =− zx+2z =⇒ z = 0 или 2z =− x+2

Для $y = z = 0$ имеем $2x2+ 2x= 0 ⇐⇒ x= 0,− 1$ , иначе $x =2 − 2z$ и

8z2 − 16z+ 8= z2 − 4+ 4z ⇐⇒ 7z2 − 20z+ 12 =0 ⇐ ⇒ z = 6 или z =2 7

Получаем тройки $(2,6,6) 7 7 7$ и $(−2,2,2)$ ,

Во втором случае $2y+ 2z = x+ 2$ , получаем

(| yz = 2x2+2x (| 8yz =16x2+ 16x { 2y2+ 2z2 = −x(y+ z)+2y+ 2z =⇒ { 4y2 +4z2 = −x2− 2x+2x +4 |( 2y+ 2z = x+2 |( 4y2 +8yz+ 4z2 =x2+ 4x+ 4

Отсюда

16x2+16x− x2+ 4= x2 +4x+ 4 ⇐⇒ 14x2 +12x= 0 ⇐⇒ x= 0,− 6 7

В первом случае $yz = 0$ , не умаляя общности, $y = 0$ , тогда $2z2 = 2z$ , откуда добавляется решение $(0,0,1)$ , а также $(0,1,0)$ для $z =0$ в силу симметрии.Bо втором $y+ z = x+2 = 47,yz = 2x2+ 2x = − 1429$ . Отсюда легко найти оставшиеся две тройки $(− 67,− 27,67),(− 67,67,− 27)$ . Проверкой убеждаемся, что они подойдут.

Ответ:

$(0,0,0),(−1,0,0),(2,6,6),(−2,2,2),(− 6,− 2,6),(− 6,6,− 2),(0,1,0),(0,0,1) 7 7 7 7 7 7 7 7 7$

Ошибка.
Попробуйте повторить позже

Задача 108#51846Максимум баллов за задание: 7

Решить систему уравнений

{ (x− 2)(x +3)= y(y − 5); log (2 − y)=-x. x y2

Подсказки к задаче

Подсказка 1

В системах уравнений, где есть какая-то кракозябра и нормальное уравнение (а это почти каждая задача с физтеха) надо сначала поработать с нормальным уравнением, как-то его попреобразовывать, чтобы оно дало нам некоторую связь на переменные, которую мы могли бы использовать для упрощения кракозябры. Посмотрим на первое уравнение, так как именно оно претендует на нормальное. Попробуйте как-то разложить данное выражение (после переноса всего в одну часть, разумеется).

Подсказка 2

Подумаем, какими теоретически могут быть скобки. У нас точно в каждой должно быть x и y, притом понятно, с какими коэффициентами. Значит, остаётся подобрать свободные коэффициенты, чтобы у нас по итогу вышло нужное количество x и y. После этого у нас будет два выражения для y через х, при том это будут линейные выражения. Останется только проверить, подходят ли они под ОДЗ, которое получается из логарифма и после подстановки. Но остается вопрос: все ли пары (x,y), которые будут таким образом получены, будут подходить под систему и ограничения, или надо проверить их на выполнение ОДЗ? Попробуйте подумать об этом в терминах достаточных и необходимых условий, а не просто подставить их в систему.

Показать ответ и решение

Первое уравнение можно записать так:

2 2 x − y + x+ 5y − 6 =0 ⇐⇒ (x+ y− 2)(x− y +3)= 0, откуда

x =y − 3 (1)

x =2 − y (2)

Из второго уравнения системы следует, что

2− y > 0,x> 0,x⁄= 1 (3)

a) Если справедливо равенство (2), то из второго уравнения системы находим $x =y2,$ откуда, используя равенство (2), получаем $2− y = y2$ или $(y− 1)(y+ 2)=0.$ Пусть $y =1,$ тогда $x= 1,$ и не выполняются условия (3). Пусть $y = −2,$ тогда $x= 4$ и $(4;−2)$ — peшение данной системы.

б) Если справедливо равенство (1) и условия (3), то $y > 3$ и $y < 2,$ что невозможно.

Ответ:

$(4;− 2)$

Ошибка.
Попробуйте повторить позже

Задача 109#79128Максимум баллов за задание: 7

Дана система неравенств

(| |x|+ |y|≤2 { x2+y2 ≥4(x+ y− 1), |( (y − 3x− 2)(3y− x+ 2)≤ 0.

Найти площадь фигуры, координаты точек которой удовлетворяют:

(a) первому неравенству системы;

(b) первым двум неравенствам системы;

Источники: Вступительные в МФТИ - 1999 (см. olymp.mipt.ru))

Подсказки к задаче

Подсказка 1

С первым неравенством всё понятно, а чтобы построить график функции из второго неравенства, нужно выделить полные квадраты. Чтобы понять, какие точки удовлетворяют третьему неравенству, нужно рассмотреть части плоскости, на которые 2 прямые её делят, и понять, какие знаки в этих частях имеет каждая из линейных функций. И всё, картинка готова!

Подсказка 2

Не забываем, что площадь сегмента находится как разность площадей соответствующего сектора и треугольника, и на этом знаний нам достаточно. Осталось внимательно найти нужные площади и радоваться жизни!

Показать ответ и решение

(a) Первому неравенству удовлетворяют точки, лежащие в квадрате (рис.) с вершинами $A(−1; 0), B(0; 1), C(1; 0), D (0; − 1).$ Площадь этого квадрата $S1 = 8.$

$PIC$

(b) Второму неравенству, которое можно записать в виде

(x− 2)2+ (y − 2)2 ≥ 4,

удовлетворяют точки, лежащие вне круга радиуса $2$ с центром в точке $E (2; 2).$

Площадь заштрихованного на рис. сегмента равна $π− 2,$ а площадь фигуры, координаты точек которой удовлетворяют первым двум неравенствам, равна

S2 = 8− (π− 2)= 10− π

(c) Прямые $y− 3x− 2 =0$ и $3y− x+ 2= 0$ пересекаются в точке $F(−1; 1)$ и проходят соответственно через точки $B$ и $C.$

Третьему неравенству удовлетворяют точки двух вертикальных углов с вершиной $F,$ один их этих углов — угол, образуемый лучами $FB$ и $FC$ и содержащий точку $O.$

Пусть $S3$ — площадь фигуры, координаты точек которой удовлетворяют всем трем неравенствам системы, $S4$ — сумма площадей треугольников $ABF$ и $CDF.$ Тогда

S4 = 1S1 =4, S3 =S2− S4 = 6− π 2

Ответ:

$(a) 8$

$(b) 10− π$

$(c) 6− π$

Ошибка.
Попробуйте повторить позже

Задача 110#101224Максимум баллов за задание: 7

Решите систему уравнений:

( x +2x + 2x +...+ 2x = 1, ||||| x1+3x2+ 4x3+...+ 4x100= 2, |{ 1 2 3 100 ||| x1+3x2+ 5x3+...+ 6x100 = 3, |||( ... x1+3x2+ 5x3+...+ 199x100 =100.

Показать ответ и решение

Давайте перепишем систему следующим образом: Сначала запишем $1$ уравнение, потом второе, из которого вычли первое, потом второе, из которого вычли третье и т.д. Получим:

(| x + 2x +2x + ...+ 2x = 1, ||||| 1 2 3 100 |||{ x2+ 2x3+2x4+ ...+ 2x100 = 1, | x3+ 2x4+2x5+ ...+ 2x100 = 1, ||||| ... |||( x99+ 2x100 = 1 x100 =1.

Видно, что $x = −1, 99$ а значит $x = 1. 98$ Заметим, что дальше продолжится это чередование. Следовательно, $x = 1 2k$ и $x = −1. 2k−1$

Ответ:

$x = 1,x = −1, 2k 2k−1$ для $k$ от $1$ до $50$

Ошибка.
Попробуйте повторить позже

Задача 111#78978Максимум баллов за задание: 7

Решить систему

(| x2 = 2∘y2-+1; { y2 = 2√z2−-1− 2; |( 2 √-2--- z = 4 x + 2− 6.

Источники: Ломоносов - 2013, 11 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Корни выглядят очень неприятно, так что давайте попробуем от них избавиться! Что для этого можно сделать?

Подсказка 2

Да, давайте обозначим каждый из корней какой-то своей буквой, например a, b, c. Тогда каждую из исходных переменных x, y, z — можно выразить через новые a, b, c! Какую систему мы тогда получим?

Подсказка 3

Мы получим систему(с точностью до обозначений): {a² - 2 = 2b; b² - 1 = 2c - 2; c² + 1=4a - 6;} Теперь остаётся придумать, что делать с этой системой...

Подсказка 4

Давайте сложим все три уравнения и перенесём всё в одну часть! Тогда можно выделить три полных квадрата, сумма которых равна нулю. Чтобы закончить решение, достаточно найти такие a, b, c, которые удовлетворяют полученному уравнению и сделать обратную замену!

Показать ответ и решение

Введём обозначения $a= √x2+-2, b= ∘y2+-1, c= √z2−-1.$ Получится система

(| a2− 2 =2b, { b2− 1= 2c− 2, |( 2 c+ 1= 4a− 6

Сложим все уравнения и перенесём в левую часть:

2 2 a +b − 4a− 2b− 2c+6 =0

(a− 2)2+(b− 1)2+ (c − 1)2 = 0

откуда $a= 2, b= 1, c= 1.$ Делаем обратную замену, получим

x= ±√2, y = 0, z = ±√2

Ответ:

$(±√2,0,±√2)$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 112#91930Максимум баллов за задание: 7

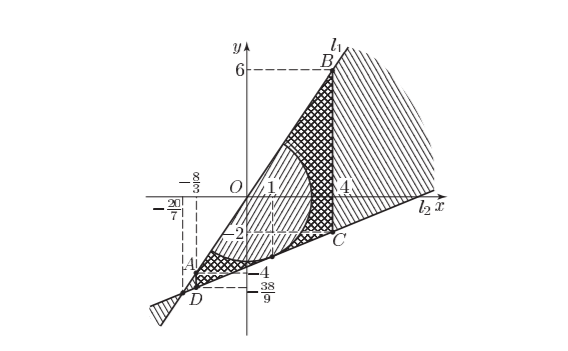
Найдите площадь фигуры $Φ$ , которая задается на координатной плоскости системой неравенств

(| x2+y2 ≥ 10 { 3x2− 4x− 32≤ 0 |( (3x− 2y)(3y− x+10)≥ 0

Показать ответ и решение

Первое неравенство определяет множество точек, лежащих вне и на границе круга с центром в точке $O (0;0)$ и радиусом $√ -- 10$ .

Решив второе неравенство, получим $8 − 3 ≤x ≤4$ . Поэтому второе неравенство задает вертикальную полосу, лежащую между прямыми $8 x =− 3$ и $x= 4$ (включая и точки этих прямых).

Наконец, третьему неравенству удовлетворяют точки множества $M$ , которое состоит из двух острых вертикальных углов, образованных прямыми $3x − 2y = 0$ и $3y− x+ 10 =0$ (включая и точки этих прямых), так как в точке $(4;0)$ , принадлежащей множеству $M$ , левая часть неравенства положительна. Множество $M$ заштриховано на рисунке ниже, а указанные прямые обозначены $l1$ и $l2$ .

Прямая $l1$ пересекается с прямыми $8 x= −3$ и $x =4$ в точках $8 A(−3;−4)$ и $B (4;6)$ , а прямая $l2$ пересекается с теми же прямыми в точках $8 38 D (− 3;−9-)$ , $C (4;−2)$ . Далее, прямая $l2$ касается окружности $x2 +y2 = 10$ , так как система уравнений